每位数据科学家应该了解的5种异常点(变化点)检测算法
作者:CSDN @ _乐多_
时间序列分析是数据科学家必须接触的主题之一。时间序列分析包括使用一系列数学工具的过程,用于研究时间序列数据,以了解发生了什么,何时以及为什么发生,以及未来可能发生的情况。
变点是时间序列数据中突然发生的变化,可能表示状态之间的转换。在处理时间序列预测用例时,检测变点是至关重要的,以便确定随机过程或时间序列的概率分布何时发生了变化。
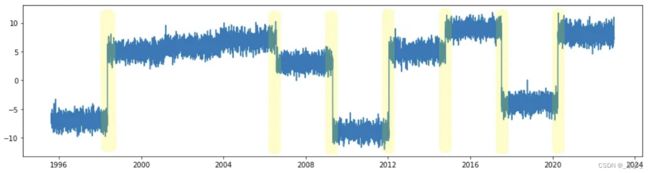 图1 样本时间序列图中可能的变点(用突出显示) 图1 样本时间序列图中可能的变点(用突出显示)
|
文章目录
-
-
- 1.分段线性回归(Piece-wise Linear Regression)
- 2.变点发现器(Change Finder)
- 3.Ruptures
- 结论
- 参考资料
-
本文将讨论并实施5种变点检测技术,并对它们的性能进行基准测试。
1.分段线性回归(Piece-wise Linear Regression)
当发生变点时,时间序列数据的模式或趋势会发生变化。分段线性回归模型的基本思想是识别不同数据区域内模式或趋势的这种变化。在存在变点的情况下,系数的值比附近区域的系数要高或低。
实现的伪代码:
1. 将时间序列数据分成x(比如说100)天的子段
2. 遍历每个子段的数据:
训练数据:枚举数据
目标数据:原始时间序列值
在训练数据和目标数据上训练一个线性回归模型
计算训练后的线性回归模型的系数
3. 绘制系数图表
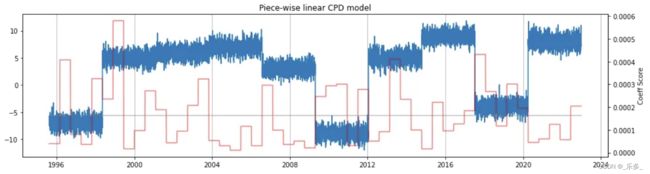 图2 线性分段变点检测算法的结果 图2 线性分段变点检测算法的结果
|
上述图片中的红线表示在该时间序列数据子段或部分上训练的每个线性回归模型的系数值。系数是乘以预测值的值,因此预测值越高,系数就越高,反之亦然。
def piece_wise_lr_cpd(data, columnName, peice_diff=100):
st_idx, end_idx = 0, peice_diff
coeff = []
while end_idx<=data.shape[0]:
X = [[x] for x in np.arange(peice_diff)]
y = list(data.iloc[list(range(st_idx, end_idx, 1))][columnName])
min_v, max_v = min(y), max(y)
y = [(x-min_v)/(max_v-min_v) for x in y]
model = LinearRegression()
model.fit(X, y)
coeff.extend([abs(model.coef_[0])]*peice_diff)
#print(data.iloc[st_idx].index, data.iloc[end_idx].index, abs(model.coef_[0]))
st_idx = end_idx
end_idx = end_idx+peice_diff
return coeff
# compute results
ts_df['coeff_1'] = piece_wise_lr_cpd(ts_df, 'series_1', peice_diff=200)
# Plot the results
fig, ax1 = plt.subplots(figsize=(16,4))
ax2 = ax1.twinx()
ax1.plot(ts_df.index, ts_df.series_1)
ax2.plot(ts_df.index, ts_df.coeff_1, color='red', alpha=0.5)
ax2.plot(ts_df.index, [np.mean(ts_df.coeff_1)]*ts_df.shape[0], color='grey', alpha=0.5)
ax1.grid(axis='x')
plt.title('Piece-wise linear CPD model')
plt.show()
2.变点发现器(Change Finder)
变点发现器是一个开源的Python包,提供实时或在线变点检测算法。它使用SDAR(Sequentially Discounting AutoRegressive)学习算法,该算法预期变点之前和之后的自回归过程将是不同的。
SDAR方法有两个学习阶段:
- 第一学习阶段:产生一个中间分数,称为异常分数(anomaly score)。
- 第二学习阶段:产生可以检测变点的变点分数(change-point score)。
 图3 变点发现器变点检测算法的结果 图3 变点发现器变点检测算法的结果
|
import changefinder
# ChangeFinder
def findChangePoints_changeFinder(ts, r, order, smooth):
'''
r: Discounting rate
order: AR model order
smooth: smoothing window size T
'''
cf = changefinder.ChangeFinder(r=r, order=order, smooth=smooth)
ts_score = [cf.update(p) for p in ts]
return ts_score
def plotChangePoints_changeFinder(df, ts, ts_score, title):
fig, ax1 = plt.subplots(figsize=(16,4))
ax2 = ax1.twinx()
ax1.plot(df.index, ts)
ax2.plot(df.index, ts_score, color='red')
ax1.set_ylabel('item sale')
ax1.grid(axis='x', alpha=0.7)
ax2.set_ylabel('CP Score')
ax2.set_title(title)
plt.show()
tsd = np.array(ts_df['series_1'])
cp_score = findChangePoints_changeFinder(tsd, r=0.01, order=3, smooth=7)
plotChangePoints_changeFinder(ts_df, tsd, cp_score, 'Change Finder CPD model')
3.Ruptures
Ruptures是一个开源的Python库,提供离线变点检测算法。该库通过分析整个序列并分割非平稳信号来检测变点。
Ruptures提供了6种算法或技术来检测时间序列数据中的变点:
- 动态规划(Dynamic Programming)
- PELT(Pruned Exact Linear Time)
- 核变化检测(Kernel Change Detection)
- 二分法分割(Binary Segmentation)
- 自底向上分割(Bottom-up Segmentation)
- 滑动窗口分割(Window Sliding Segmentation)
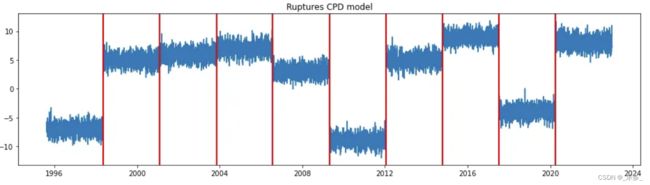 图4 ruptures变点检测算法的结果 图4 ruptures变点检测算法的结果
|
import ruptures as rpt
def plot_change_points_ruptures(df, ts, ts_change_all, title):
plt.figure(figsize=(16,4))
plt.plot(df.index, ts)
for x in [df.iloc[idx-1].name for idx in ts_change_all]:
plt.axvline(x, lw=2, color='red')
plt.title(title)
plt.show()
tsd = np.array(ts_df['series_1'])
detector = rpt.Pelt(model="rbf").fit(tsd)
change_points = detector.predict(pen=3) #penalty
plot_change_points_ruptures(ts_df, tsd, change_points[:-1], 'Ruptures CPD model for series_1')
结论
在本文中,我们讨论了3种流行的实用技术,用于识别时间序列数据中的变点。变点检测算法具有各种应用,包括医疗条件监测、人类活动分析、网站追踪等。
除了上述讨论的变点检测算法外,还有其他监督和无监督的变点检测算法。
参考资料
Change finder文档:https://pypi.org/project/changefinder/
Ruptures文档:https://centre-borelli.github.io/ruptures-docs/
声明:
本人作为一名作者,非常重视自己的作品和知识产权。在此声明,本人的所有原创文章均受版权法保护,未经本人授权,任何人不得擅自公开发布。
本人的文章已经在一些知名平台进行了付费发布,希望各位读者能够尊重知识产权,不要进行侵权行为。任何未经本人授权而将付费文章免费或者付费(包含商用)发布在互联网上的行为,都将视为侵犯本人的版权,本人保留追究法律责任的权利。
谢谢各位读者对本人文章的关注和支持!