本质矩阵 基础矩阵 单应矩阵 (1)

本质矩阵 基础矩阵 单应矩阵

基本概念：

本质矩阵E（Essential Matrix）：反映【空间一点P的像点】在【不同视角摄像机】下【摄像机坐标系】中的表示之间的关系。

基础矩阵F（Fundamental Matrix）：反映【空间一点P的像素点】在【不同视角摄像机】下【图像坐标系】中的表示之间的关系。

ORB-SLAM点云地图中相机的位姿初始化，无论算法工作在平面场景，还是非平面场景下，都能够完成初始化的工作。其中主要是使用了适用于平面场景的单应性矩阵H和适用于非平面场景的基础矩阵F，程序中通过一个评分规则来选择适合的模型，恢复相机的旋转矩阵R和平移矩阵t。

对极几何（Epipolar Geometry）描述的是两幅视图之间的内在射影关系，与外部场景无关，只依赖于摄像机内参数和这两幅视图之间的相对位姿。

1.当相机为单目时，我们只知道2D的像素坐标，因而问题是根据两组2D点估计运动。该问题用对极几何来解决。
2.当相机为双目、RGB-D时，或者我们通过某种方法得到了距离信息，那问题就是根据两组3D点估计运动。该问题通常用ICP来解决。
3.如果我们有3D点和它们在相机的投影位置，也能估计相机的运动。该问题通过PnP求解。

2D-2D: 对极几何

现在，假设我们从两张图像中，得到了一对配对好的特征点。

如果我们有若干对这样的匹配点，就可以通过这些二维图像点的对应关系，恢复出在两帧之间摄像机的运动。

这里“若干对”具体是多少对呢？我们会在下文介绍。先来看看两个图像当中的匹配点有什么几何关系吧。

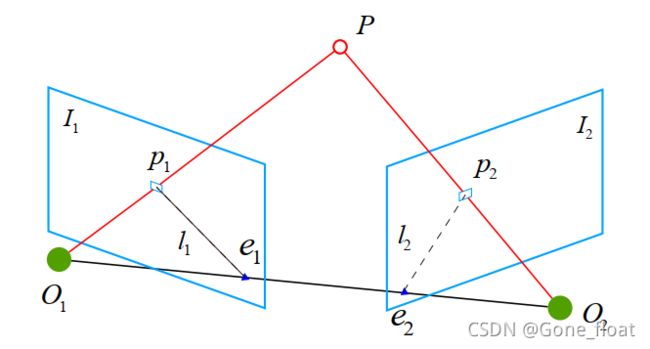
我们希望求取两帧图像 $I1,I2$ 之间的运动，设第一帧到第二帧的运动为$R,t$。两个相机中心分别为 $O1,O2$。现在，考虑 $I1$ 中有一个特征点 $p1$，它在 $I2$ 中对应 特征点 $p2$。我们知道这俩是通过特征匹配得到的。如果匹配正确，说明它们确实是同一个空间点在两个成像平面上的投影。

这里我们需要一些术语来描述它们之间的几何关系。

极平面: 首先，连线 $O_1{p}_1$ 和连线 $O_2{p}_2$ 在三维空间中会相交于点 $P$。这时候点 $O1,O2,P$ 三个点可以确定一个平面，称为极平面（Epipolar plane） 。

$O1O2$ 连线与像平面 $I1,I2$ 的交点分别为 $e1,e2$。 $e1,e2$称为极点（Epipoles），$O1O2$ 被称为基线（Baseline） 。

极平面与两个像平面 $I1,I2$ 之间的相交线 $l1,l2$ 为极线（Epipolar line） 。

直观上讲，从第一帧的角度上看，射线 $O_1{p}_1$ 是某个像素可能出现的空间位置——因为该射线上的所有点都会投影到同一个像素点。同时，如果不知道 P 的位置，那么当我们在第二个图像上看时，连线 $e_2{p}_2$（也就是第二个图像中的极线）就是 $P$ 可能出现的投影的位置，也就是射线 $O_1{p}_1$ 在第二个相机中的投影。

现在，由于我们通过特征点匹配，确定了 $p2$ 的像素位置，所以能够推断 $P$ 的空间位置，以及相机的运动。要提醒读者的是， 这都是多亏了正确的特征匹配。如果没有特征匹配，我们就没法确定 $p2$ 到底在极线的哪个位置了。那时，就必须在极线上搜索以获得正确的匹配。

现在，我们从代数角度来看一下这里出现的几何关系。在第一帧的坐标系下，设 $P$ 的空间位置为：

$\mathbf{P}=[X,Y,Z{]}^T$

根据针孔相机模型，我们知道两个像素点 $p_1,p_2$的像素位置为

$s_1{\mathbf{p}}_1=\mathbf{K}\mathbf{P},s_2{\mathbf{p}}_2=\mathbf{K}(\mathbf{R}\mathbf{P}+\mathbf{t})$

这里 $K$ 为相机内参矩阵， $R,t$ 为两个坐标系的相机运动（如果我们愿意，也可以写成李代数形式）。具体来说，这里计算的是$R_{21},t_{21}$。$s_1,s_2$代表尺度。

有时，我们会用齐次坐标表示像素点。在使用齐次坐标时，一个向量将等于它自身乘上任意的非零常数。这通常用于表达一个投影关系。例如，$s_1{p}_1$ 和 $p_1$ 成投影关系，它们在齐次坐标的意义下是相等的。我们称这种相等关系为尺度意义下相等(equal up to a scale), 记作：

$sp\simeq p$

那么，上述两个投影关系写为：

${\mathbf{p}}_1\simeq KP,p_2\simeq K(RP+t)$

现在，取：

${\mathbf{x}}_1={\mathbf{K}}^{-1}{\mathbf{p}}_1,{\mathbf{x}}_2={\mathbf{K}}^{-1}{\mathbf{p}}_2$

这里的 $x1,x2$ 是两个像素点的归一化平面(相当于相机坐标系 $Z=1$平面上的点)上的坐标。代入上式，得：

$x_2\simeq R{x}_1+t$

两边同时左乘 $t^{\wedge }$。回忆 $\wedge$ 的定义，这相当于两侧同时与 t 做外积：

${\mathbf{t}}^{\wedge }{\mathbf{x}}_2={\mathbf{t}}^{\wedge }\mathbf{R}{\mathbf{x}}_1$

然后，两侧同时左乘${\mathbf{x}}_2^T$ ：

${\mathbf{x}}_2^T{\mathbf{t}}^{\wedge }{\mathbf{x}}_2={\mathbf{x}}_2^T{\mathbf{t}}^{\wedge }\mathbf{R}{\mathbf{x}}_1$

观察等式左侧， ${\mathbf{t}}^{\wedge }{\mathbf{x}}_2$ 是一个与 $t$ 和 ${\mathbf{x}}_2$ 都垂直的向量。把它再和 ${\mathbf{x}}_2$ 做内积时，将得到 0。由于等式左侧严格为0，乘以任何非零常数之后也为0，于是我们可以把 $\simeq$ 写成通常的符号。因此，我们就得到了一个简洁的式子：

${\mathbf{x}}_2^T{\mathbf{t}}^{\wedge }\mathbf{R}{\mathbf{x}}_1=0$

重新代入 $p_1$,$p_2$

${\mathbf{p}}_2^T{\mathbf{K}}^{-T}{\mathbf{t}}^{\wedge }\mathbf{R}{\mathbf{K}}^{-1}{\mathbf{p}}_1=0$

这两个式子都称为对极约束，它以形式简洁著名。它的几何意义是 $O1,P,O2$ 三者共
面。对极约束中同时包含了平移和旋转。

我们把中间部分记作两个矩阵：基础矩阵（Fundamental Matrix） F 和本质矩阵（Essential Matrix） E，可以进一步简化对极约束：

$\mathbf{E}={\mathbf{t}}^{\wedge }\mathbf{R},\mathbf{F}={\mathbf{K}}^{-T}\mathbf{E}{\mathbf{K}}^{-1},{\mathbf{x}}_2^T\mathbf{E}{\mathbf{x}}_1={\mathbf{p}}_2^T\mathbf{F}{\mathbf{p}}_1=0$

对极约束简洁地给出了两个匹配点的空间位置关系。于是，相机位姿估计问题变为以下两步：

1. 根据配对点的像素位置，求出 $E$ 或者 $F$；
2. 根据 $E$ 或者 $F$，求出 $R,t$。

由于 $E$ 和 $F$ 只相差了相机内参，而内参在 SLAM 中通常是已知的，所以实践当中往往使用形式更简单的 $E$。

https://www.zhihu.com/question/27581884
https://www.cnblogs.com/YongQiVisionIMAX/p/9711273.html
视觉SLAM十四讲
https://www.pianshen.com/article/2772299087/
https://www.guyuehome.com/34324

1.已知一幅图像中一点，如何寻找另一幅图像中这个点的对应点（可用光流法、特征点匹配法）

2.已知两幅图像中两点是对应关系，如何求解两相机的相对位置和姿态【R|t】

3.已知多幅图像中同一3D点的对应点，如何求解该3D点的3D坐标

这种极线约束的外点检测方法在动态场景下的SLAM中尤为常见，可以有效地检测出运动物体上的外点，具体做法为：

1. 用RANSAC算法计算两帧图像的基础矩阵F；
2. 对于第一帧图像每一特征点p1，利用基础矩阵计算其投影后的极线e2p2所在直线的参数；
3. 计算对应特征点p2到该极线的距离，若过大，则为外点。
   当然这种算法也有不足之处，当物体沿着极线运动时，到该极线的距离始终为0，无法反映出其真是误差。这种弊端在检测高速公路上行驶的汽车时尤为明突出。