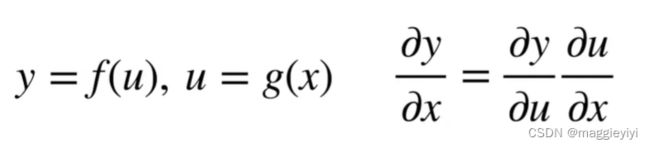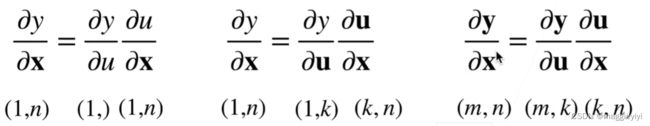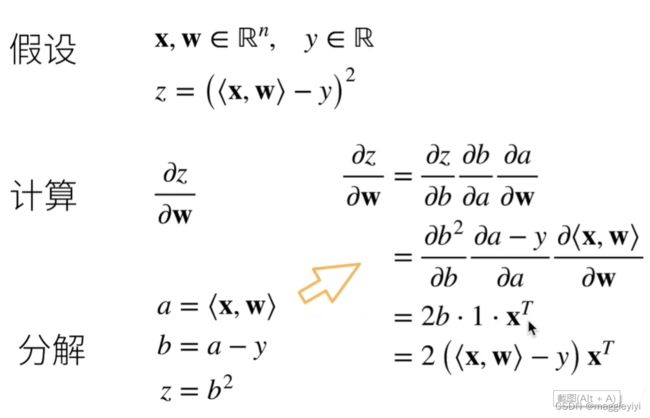线性回归原理(李沐老师学习笔记)
目录
1 线性回归的定义
1.1 线性回归的基本元素
1.1.1 线性模型
1.1.2 损失函数
1.1.3 为什么传统线性回归解不能应用于深度学习
1.1.4 随机梯度下降
2 自动求导
2.1 标量链式法则
2.2 标量对向量求导
2.3 自动求导
2.3.1 反向积累
3 矢量化加速(整体小样本)
4 线性回归和深度学习的联系
1 线性回归的定义
回归(regression)是能为一个或多个自变量与因变量之间关系建模的一类方法。 在自然科学和社会科学领域,回归经常用来表示输入和输出之间的关系。
应用领域:股票、房价、工业等
1.1 线性回归的基本元素
假设前提:
- 自变量x和因变量y之间的关系是线性的, 即y可以表示为x中元素的加权和,这里通常允许包含观测值的一些噪声;
- 我们假设任何噪声都比较正常,如噪声遵循正态分布
例如:最常见的线性回归 y=kx+b;
通常,我们使用n来表示数据集中的样本数。 对索引为i的样本,其输入表示为x(i)=[x1(i),x2(i)]⊤, 其对应的标签是y(i)。
1.1.1 线性模型
线性假设是指目标,可以表示为特征的加权和,如下面的式子:
![]()
其中,k1、k2称为权重(weight),b称为偏置(bais),权重决定了每个特征对我们预测值的影响,偏置是指当所有特征都取值为0时,预测值应该为多少。
应用:给定一个数据集,我们的目标是寻找模型的权重w和偏置b, 使得根据模型做出的预测大体符合数据里的真实价格。 输出的预测值由输入特征通过线性模型的仿射变换决定,仿射变换由所选权重和偏置确定。
(注:输入特征的一个 仿射变换(affine transformation)。 仿射变换的特点是通过加权和对特征进行线性变换(linear transformation), 并通过偏置项来进行平移(translation)。)
现实:现实生活中,我们的数据集普遍是高维度的,因此在建模时,线性代数的表达法可读性更好。
当我们的输入包含d个特征时,我们将预测结果y^ (通常使用“尖角”符号表示y的估计值)表示为:
![]()
也可以更简洁地用:![]()
在开始寻找最好的模型参数(model parameters)w和b之前, 我们还需要两个东西:
(1)一种模型质量的度量方式; (损失函数)
(2)一种能够更新模型以提高模型预测质量的方法。(随机梯度下降)
1.1.2 损失函数
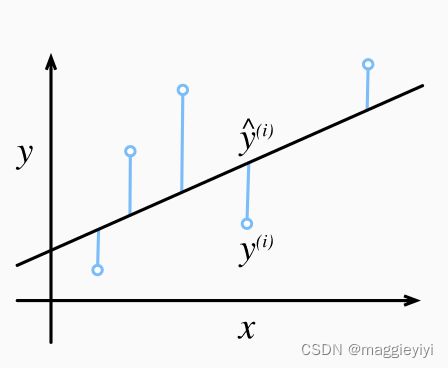
损失函数可以用来衡量数据预测值和真实值之间的拟合程度,能够量化目标的实际值与预测值之间的差距。 通常我们会选择非负数作为损失,且数值越小表示损失越小,完美预测时的损失为0。 回归问题中最常用的损失函数是平方误差函数。
当样本i的预测值为y^(i),其相应的真实标签为y(i)时, 平方误差可以定义为以下公式:
![]()
常数1/2不会带来本质的差别,但这样在形式上稍微简单一些 (因为当我们对损失函数求导后常数系数为1)。
为了度量模型在整个数据集上的质量,我们需计算在训练集n个样本上的损失均值(也等价于求和)。
![]()
那么,找到可以让线性回归拟合度最好的参数(w,b)满足:
![]()
1.1.3 为什么传统线性回归解不能应用于深度学习
这里用李沐老师的解释来回答:
1.1.4 随机梯度下降
梯度下降(gradient descent):它通过不断地在损失函数递减的方向上更新参数来降低误差。
梯度下降最简单的用法是计算损失函数(数据集中所有样本的损失均值) 关于模型参数的导数(在这里也可以称为梯度)。 但实际中的执行可能会非常慢:因为在每一次更新参数之前,我们必须遍历整个数据集。 因此,我们通常会在每次需要计算更新的时候随机抽取一小批样本, 这种变体叫做小批量随机梯度下降(minibatch stochastic gradient descent)。
在每次迭代中,我们首先随机抽样一个小批量B, 它是由固定数量的训练样本组成的。 然后,我们计算小批量的平均损失关于模型参数的导数(也可以称为梯度)。 最后,我们将梯度乘以一个预先确定的正数η,并从当前参数的值中减掉。
![]()
注意:估计值不会使损失函数真正地达到最小值,算法会使得损失向最小值缓慢收敛,但却不能在有限的步数内非常精确地达到最小值。
什么是泛化(generalization)?找到一组参数,这组参数能够在我们从未见过的数据上实现较低的损失
2 自动求导
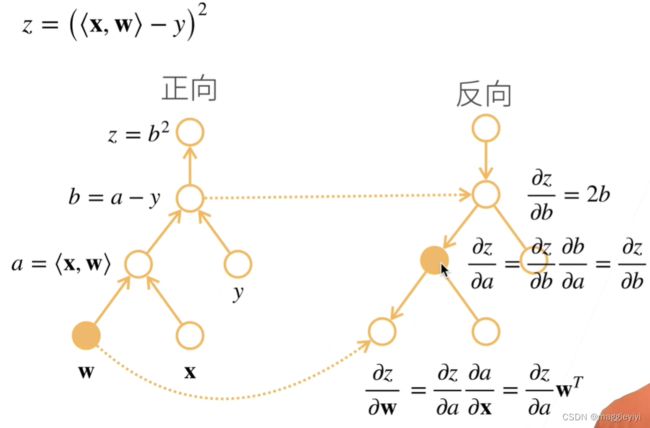
向量链式法则:
2.1 标量链式法则
2.2 标量对向量求导
例子1:
例子2:
2.3 自动求导
自动求导计算一个函数在制定值上的导数
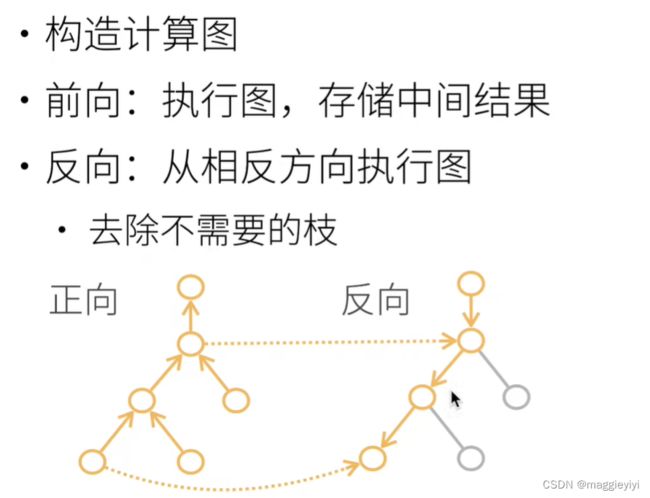
step 1: 将代码分解成操作子
step 2:将计算表示成一个无环图:
2.3.1 反向积累
3 矢量化加速(整体小样本)
在训练我们的模型时,我们经常希望能够同时处理整个小批量的样本。 为了实现这一点,需要我们对计算进行矢量化, 从而利用线性代数库,而不是在Python中编写开销高昂的for循环。
import math
import time
import numpy as np
import torch
from d2l import torch as d2l
n = 10000
a = torch.ones(n)
b = torch.ones(n)
d = a + b4 线性回归和深度学习的联系
可以将线性回归看成一层的神经网络,如下图所示:
输入为x1,…,xd, 因此输入层中的输入数(或称为特征维度,feature dimensionality)为d。 网络的输出为o1,因此输出层中的输出数是1。
对于线性回归,每个输入都与每个输出(在本例中只有一个输出)相连, 我们将这种变换中的输出层) 称为全连接层(fully-connected layer)或称为稠密层(dense layer)。 下一章将详细讨论由这些层组成的网络。