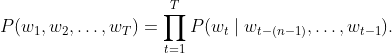文本预处理，语言模型，循环神经网络

文本预处理

文本是一类序列数据，一篇文章可以看作是字符或单词的序列，本节将介绍文本数据的常见预处理步骤，预处理通常包括四个步骤：

1. 读入文本
2. 分词
3. 建立字典，将每个词映射到一个唯一的索引（index）
4. 将文本从词的序列转换为索引的序列，方便输入模型

用现有工具进行分词

spaCy，NLTK, jieba。

 

语言模型

一段自然语言文本可以看作是一个离散时间序列，给定一个长度为TT的词的序列w1,w2,…,wT，语言模型的目标就是评估该序列是否合理，即计算该序列的概率：

P(w1,w2,…,wT).

本节我们介绍基于统计的语言模型，主要是n元语法（n-gram）。在后续内容中，我们将会介绍基于神经网络的语言模型。

语言模型

假设序列w1,w2,…,wT中的每个词是依次生成的，我们有

例如，一段含有4个词的文本序列的概率

                           P(w1,w2,w3,w4)=P(w1)P(w2∣w1)P(w3∣w1,w2)P(w4∣w1,w2,w3).

语言模型的参数就是词的概率以及给定前几个词情况下的条件概率。设训练数据集为一个大型文本语料库，如维基百科的所有条目，词的概率可以通过该词在训练数据集中的相对词频来计算，例如，w1的概率可以计算为：

                                                                    

其中n(w1)为语料库中以w1作为第一个词的文本的数量，n为语料库中文本的总数量。

类似的，给定w1情况下，w2的条件概率可以计算为：

                                                                   

其中n(w1,w2)为语料库中以w1作为第一个词，w2作为第二个词的文本的数量。

n元语法

序列长度增加，计算和存储多个词共同出现的概率的复杂度会呈指数级增加。nn元语法通过马尔可夫假设简化模型，马尔科夫假设是指一个词的出现只与前面nn个词相关，即nn阶马尔可夫链（Markov chain of order nn），如果n=1，那么有。基于n−1阶马尔可夫链，我们可以将语言模型改写为

                                                       

以上也叫n元语法（n-grams），它是基于n−1阶马尔可夫链的概率语言模型。例如，当n=2时，含有4个词的文本序列的概率就可以改写为：

                                        

当n分别为1、2和3时，我们将其分别称作一元语法（unigram）、二元语法（bigram）和三元语法（trigram）。例如，长度为4的序列w1,w2,w3,w4在一元语法、二元语法和三元语法中的概率分别为

                                            

当n较小时，n元语法往往并不准确。例如，在一元语法中，由三个词组成的句子“你走先”和“你先走”的概率是一样的。然而，当n较大时，n元语法需要计算并存储大量的词频和多词相邻频率。

思考：n元语法可能有哪些缺陷？

1. 参数空间过大
2. 数据稀疏

循环神经网络

    理解：循环神经网络可以看成是一个过程，通过现在的发生的事情来预测未来发生的事，t时刻的输出由t-1时刻的隐藏层输出Ht-1和t时刻的输入Xt共同决定。(Xt,Ht-1) -----> Yt

递归网络问题

 常规递归网络从理论上应该可以顾及所有过去时刻的依赖，然而实际却无法按人们所想象工作。原因在于梯度消失（vanishinggradient）和梯度爆炸（exploding gradient）问题。

解决办法：裁剪梯度

裁剪梯度

      循环神经网络中较容易出现梯度衰减或梯度爆炸，这会导致网络几乎无法训练。裁剪梯度（clip gradient）是一种应对梯度爆炸的方法。假设我们把所有模型参数的梯度拼接成一个向量 g，并设裁剪的阈值是θ。裁剪后的梯度的L2范数不超过θ。

                                                                                    

def grad_clipping(params, theta, device):
    norm = torch.tensor([0.0], device=device)
    for param in params:
        norm += (param.grad.data ** 2).sum()
    norm = norm.sqrt().item()
    if norm > theta:
        for param in params:
            param.grad.data *= (theta / norm)