LeetCode Cookbook 数学（1）

CSDN话题挑战赛第2期
参赛话题：算法题解

LeetCode Cookbook 数学（1）

   本节是与数学相关的习题，难题放在下一节，这一节都是简单题，喜欢的话，点赞收藏哦！
 

7. 整数反转（model-I 数字本身操作）

题目链接：7. 整数反转
题目大意：给你一个 32 位的有符号整数 x ，返回将 x 中的数字部分反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 $[-2^{31},2^{31}-1]$ ，就返回 0。
假设环境不允许存储 64 位整数（有符号或无符号）。

例如：

输入：x = 123
输出：321

输入：x = -123
输出：-321

输入：x = 120
输出：21

输入：x = 0
输出：0

• 解题思路：while 循环处理就可以了 区间边界的细节注意
• 时间复杂度：$O(log(|x|))$ 翻转的次数即 x 十进制的位数。
• 空间复杂度：$O(1)$

class Solution:
    def reverse(self, x: int) -> int:
        INT_MIN,INT_MAX = -2**31,2**31-1
        flag = 1 if x<0 else 0
        x = abs(x)
        ans = 0
        while x:
            tmp = x%10
            x //= 10
            ans = ans*10+tmp
        ans = -ans if flag else ans
        if (ans>INT_MAX) or (ans<INT_MIN): ans = 0
        return ans

 

9. 回文数（model-I 数字本身操作）

题目链接：9. 回文数
题目大意：给你一个整数 x ，如果 x 是一个回文整数，返回 true ；否则，返回 false 。
回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。
例如，121 是回文，而 123 不是。

例如：

输入：x = 121
输出：true

输入：x = -121
输出：false
解释：从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。

输入：x = 10
输出：false
解释：从右向左读, 为 01 。因此它不是一个回文数。

• 解题思路：有些耍赖的办法
• 时间复杂度：$O(N)$ N为字符串长度
• 空间复杂度：$O(N)$

class Solution:
    def isPalindrome(self, x: int) -> bool:
        s = str(x)
        return True if s[::-1] == s else False

 

172. 阶乘后的零 （model-I 数字本身操作）

题目链接：172. 阶乘后的零
题目大意：给定一个整数 n ，返回 n! 结果中尾随零的数量。
提示 $n!=n\ast (n-1)\ast (n-2)\ast ...\ast 3\ast 2\ast 1$

例如：

输入：n = 3
输出：0
解释：3! = 6 ，不含尾随 0

输入：n = 5
输出：1
解释：5! = 120 ，有一个尾随 0

输入：n = 0
输出：0

• 解题思路： 贪心 找因子5的个数
• 时间复杂度：$O(N)$ N为n!中因子 5 的个数
• 空间复杂度：$O(1)$

class Solution:
    def trailingZeroes(self, n: int) -> int:
        ans = 0
        while n:
            n //= 5
            ans += n
        return ans

258. 各位相加（model-I 数字本身操作）

题目链接：258. 各位相加
题目大意：给定一个非负整数 num，反复将各个位上的数字相加，直到结果为一位数。返回这个结果。

例如：

输入: num = 38
输出: 2 
解释: 各位相加的过程为：
38 --> 3 + 8 --> 11
11 --> 1 + 1 --> 2
由于 2 是一位数，所以返回 2。

输入: num = 0
输出: 0

• 解题思路： 用 while 循环来处理
• 时间复杂度：$O(log(n))$ n为整数值
• 空间复杂度：$O(1)$

class Solution:
    def addDigits(self, num: int) -> int:
        
        # return (num-1) % 9 + 1 if num else num
        
        while num>9:
            cur = 0
            while num:
                cur += num%10
                num //= 10
            num = cur
        return num

 

263. 丑数（model-I 数字本身操作）

题目链接：263. 丑数
题目大意：丑数 就是只包含质因数 2、3 和 5 的正整数。
给你一个整数 n ，请你判断 n 是否为 丑数 。如果是，返回 true ；否则，返回 false 。

例如：

输入：n = 6
输出：true
解释：6 = 2 × 3

输入：n = 1
输出：true
解释：1 没有质因数，因此它的全部质因数是 {2, 3, 5} 的空集。习惯上将其视作第一个丑数。

输入：n = 14
输出：false
解释：14 不是丑数，因为它包含了另外一个质因数 7 。

• 解题思路：建立满足要求的因子集合 用 while 循环来处理
• 时间复杂度：$O(log(n))$ n为整数值
• 空间复杂度：$O(1)$

class Solution:
    def isUgly(self, n: int) -> bool:
        if n<1: return False
        factor = [2,3,5]
        for i in factor:
            # Be sober!
            while n % i == 0:
                n //= i 
        if n == 1: return True
        return False

 

507. 完美数（model-I 数字本身操作）

题目链接：507. 完美数
题目大意：对于一个 正整数，如果它和除了它自身以外的所有 正因子 之和相等，我们称它为 「完美数」。
给定一个 整数 n， 如果是完美数，返回 true；否则返回 false。

例如：

输入：num = 28
输出：true
解释：28 = 1 + 2 + 4 + 7 + 14
1, 2, 4, 7, 和 14 是 28 的所有正因子。

输入：num = 7
输出：false

• 解题思路：打表.
• 时间复杂度：$O(1)$
• 空间复杂度：$O(1)$

class Solution:
    def checkPerfectNumber(self, num: int) -> bool:
        return num==6 or num==28 or num==496 or num==8128 or num==33550336

 

202. 快乐数（model-I 数字本身操作）

题目链接：202. 快乐数
题目大意：编写一个算法来判断一个数 n 是不是快乐数。
「快乐数」 定义为：

• 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
• 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
• 如果这个过程 结果为 1，那么这个数就是快乐数。
  如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

例如：

输入：n = 19
输出：true
解释：
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

输入：n = 2
输出：false

• 解题思路：快慢指针处理的手段 非常地妙
• 时间复杂度：$O(log(n))$
• 空间复杂度：$O(1)$

class Solution:
    def isHappy(self, n: int) -> bool:

        def get_nxt(num: int) -> int:
            tSum = 0
            while num>0:
                num,dig = divmod(num,10)
                tSum += dig**2
            return tSum
        
        slow,fast = n,get_nxt(n)
        while fast != 1 and slow != fast:
            slow = get_nxt(slow)
            fast = get_nxt(get_nxt(fast))
        return fast == 1  

 

1137. 第 N 个泰波那契数（model-I 数字本身操作）

题目链接：1137. 第 N 个泰波那契数
题目大意：泰波那契序列 Tn 定义如下：
$T_0=0,T_1=1,T_2=1$, 且在 n >= 0 的条件下 $T_{n+3}=T_n+T_{n+1}+T_{n+2}$
给你整数 n，请返回第 n 个泰波那契数 T_n 的值。

例如：

输入：n = 4
输出：4
解释：
T_3 = 0 + 1 + 1 = 2
T_4 = 1 + 1 + 2 = 4

输入：n = 25
输出：1389537

• 解题思路：预设好做就可以了。
• 时间复杂度：$O(N)$ N为数组长度
• 空间复杂度：$O(1)$

class Solution:
    def tribonacci(self, n: int) -> int:
        if n<2: return n
        a,b,c = 0,1,1
        while n>2:
            c,b,a = a+b+c,c,b
            n -= 1
        return c

 

1154. 一年中的第几天（model-I 数字本身操作）

题目链接：1154. 一年中的第几天
题目大意：给你一个字符串 date ，按 YYYY-MM-DD 格式表示一个 现行公元纪年法 日期。返回该日期是当年的第几天。

例如：

输入：date = "2019-01-09"
输出：9
解释：给定日期是2019年的第九天。

输入：date = "2019-02-10"
输出：41

• 解题思路：这道题 的范围贼坑 注意 年份需要好好判断。
• 时间复杂度：$O(1)$
• 空间复杂度：$O(1)$

class Solution:
    def dayOfYear(self, date: str) -> int:
        amount = [31,28,31,30,31,30,31,31,30,31,30,31]
        year,mon,day = [int(x) for x in date.split('-')]
        if year%400==0 or (year%4==0 and year%100!=0):
            amount[1] += 1
        ans = sum(amount[:(mon-1)])
        return ans+day

 

1281. 整数的各位积和之差（model-I 数字本身操作）

题目链接：1281. 整数的各位积和之差
题目大意：给你一个整数 n，请你帮忙计算并返回该整数「各位数字之积」与「各位数字之和」的差。

例如：

输入：n = 234
输出：15 
解释：
各位数之积 = 2 * 3 * 4 = 24 
各位数之和 = 2 + 3 + 4 = 9 
结果 = 24 - 9 = 15

输入：n = 4421
输出：21
解释： 
各位数之积 = 4 * 4 * 2 * 1 = 32 
各位数之和 = 4 + 4 + 2 + 1 = 11 
结果 = 32 - 11 = 21

• 解题思路： 按题意做就可以。
• 时间复杂度：$O(logN)$ N为整数
• 空间复杂度：$O(1)$

class Solution:
    def subtractProductAndSum(self, n: int) -> int:
        s,t = 0,1
        while n:
            tmp = n%10
            s += tmp
            t *= tmp
            n //= 10
        return t-s

 

812. 最大三角形面积（model-II 几何）

题目链接：812. 最大三角形面积
题目大意：给定包含多个点的集合，从其中取三个点组成三角形，返回能组成的最大三角形的面积。

例如：

示例:
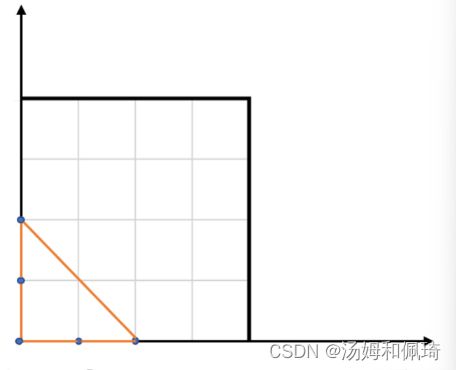
输入: points = [[0,0],[0,1],[1,0],[0,2],[2,0]]
输出: 2
解释: 
这五个点如下图所示。组成的橙色三角形是最大的，面积为2。

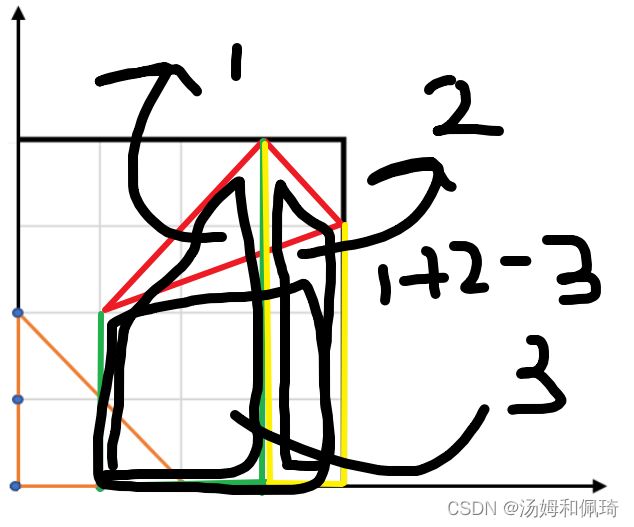
• 解题思路： 三个梯形求解
• 时间复杂度：$O(N^3)$ N为数组长度
• 空间复杂度：$O(1)$

class Solution:
    def largestTriangleArea(self, points: List[List[int]]) -> float:
        ans = 0
        N = len(points)
        for i in range(N-2):
            for j in range(i+1,N-1):
                for k in range(i+2,N):
                    (x1,y1),(x2,y2),(x3,y3) = points[i],points[j],points[k]
                    # decompose into three trapezoids operation
                    # 分解成三个梯形之间的运算
                    ans = max(ans,0.5*abs(x1*y3-x1*y2+x2*y1-x2*y3+x3*y2-x3*y1))
        return ans

总结

   努力 奋斗！要写大论文 啊~ 要命。