TOP K问题解法整理（C++实现）

---

前言

本文记录了针对各厂面试中常出的TOP K问题（求最大/最小的第K个元素）的各种解法。限于笔者实力不足，本文仅罗列笔者能够手写出的算法实现（欢迎补充）

---

一、top K问题是什么？

在一堆数据里面找到前 K大/小的数。常见面试题出法：最大（小）K个数，前K个高频元素，第K个最大（小）元素。
具体有：有整数数组 a[8] = {4，5，1，6，2，7，3，8}这8个数字，则前4（K）大的数字为8，7，6，5这几个数字。

二、解法

1.基础中的基础解法

要找前K大或者前K小的数，首先想到的方法就是将所有数据整体进行一个排序，然后输出前K个或者后K个（前n-K）个数据。

代码如下（示例）：

#include 
#include 
#include 
using namespace std;

void QuickSort(vector<int> &v, int start, int end)
{
	int i = start;
	int j = end;
	if (i<j)
	{
		int temp = v[i];
		while (i<j)
		{
			while (i<j && temp>v[j])
			{
				j--;
			}
			if (i<j)
			{
				v[i] = v[j];
				i++;
			}
			while (i<j && temp<v[i])
			{
				i++;
			}
			if (i<j)
			{
				v[j] = v[i];
			}
		}
		v[i] = temp;
		QuickSort(v, start, i - 1);
		QuickSort(v, i + 1, end);
	}
	return;
}

bool compare(int a, int b)
{
	return a > b;
}

int main()
{
	//创建测试用例
	vector<int> v = { 4,5,1,6,2,7,3,8 };
	int k = 4;

	//排序：标准库函数排序；快速排序
	//sort(v.begin(), v.end(), compare);
	QuickSort(v,0,v.size()-1);

	//输出
	for (int i = 0; i < k; i++)
	{
		cout << v[i] << endl;
	}

	system("pause");
	return 0;
}

这里可以应用STL的sort方法结合仿函数进行排序，也可以手写快速排序进行排序。其时间复杂度为快排的复杂度和找遍历前K个元素的复杂度
O(nlogn)+O(K)=O(nlogn)
实际上这种方法不会被采用，主要原因在于快速排序算法做了很多问题外的无用功，即对其余不需要的数也进行了排序，浪费了很多时间。

2.进阶一：局部冒泡

从基础解法出发，我们开始思索如何避免时间资源的浪费。即如何避免对不需要的部分做排序（无用功）。从排序的角度思索，很容易想到使用不完全冒泡排序，或者叫局部冒泡排序。找到我们需要的K个元素后，排序即停止。
代码如下（示例）：

#include 
#include 
#include 
using namespace std;

void PartialBubbleSort(vector<int> &v, int k)
{
	for (int i = 0; i < k; i++)
	{
		for (int j = 0; j < v.size()-i-1; j++)
		{
			if (v[j] > v[j+1])
			{
				v[j] = v[j] + v[j + 1];
				v[j + 1] = v[j] - v[j + 1];
				v[j] = v[j] - v[j + 1];
			}
		}
	}
	return;
}

int main()
{
	//创建测试用例
	vector<int> v = { 4,5,1,6,2,7,3,8 };
	int k = 4;

	//局部冒泡排序
	PartialBubbleSort(v,k);

	//输出
	for (int i = 0; i < k; i++)
	{
		cout << v[v.size() - 1 - i] << endl;
	}

	system("pause");
	return 0;
}

时间复杂度O(nK)。

3.进阶二：快速选择

当然从快速排序出发很容易联想到一种特殊情况：快排的每一轮（partition）都是找一个基准值，然后排序的结果是基准值左边的都小于基准值，基准值的右边都大于基准值（从小到大排序）那么如果恰巧这个基准值就是第K个值，岂不美哉。
这就引出快速选择算法，即我们要努力找到这个“完美”的基准值。
所以在快速排序的基础上，我们仅仅需要在每执行一次快排的时候，比较基准值位置是否在n-K的位置上：如果小于n-K，则第 k 个最大值在基准值的右边，我们只需递归快速排序基准值右边的子序列即可；如果大于n-K，同理递归左边的子序列；如果等于 n-k ，则第 k 个最大值就是基准值。
代码如下（在快速排序的基础上进行改进）：

void QuickSelect(vector<int> &v, int start, int end,int k)
{
	int i = start;
	int j = end;
	if (i < j)
	{
		int temp = v[i];
		while (i < j)
		{
			while (i<j && temp>v[j])
			{
				j--;
			}
			if (i < j)
			{
				v[i] = v[j];
				i++;
			}
			while (i < j && temp < v[i])
			{
				i++;
			}
			if (i < j)
			{
				v[j] = v[i];
			}
		}
		v[i] = temp;
		if (i == k)
		{
			return;
		}
		else if(i < k)
		{
			QuickSelect(v, i + 1, end, k);
		}
		else
		{
			QuickSelect(v, start, i - 1, k);
		}
	}
	return;
}

算法复杂度O(n)

3.进阶三：构造小顶堆/大顶堆

其实每个出Top K的面试题出题人，都是在期望这个答案。（基于我微薄的面试经验…）其实我一开始是很恐惧使用堆，但是熟悉之后还是总结出一点经验，这里我尽量解释得明白。
其实相较于前面几个方法，利用堆一个显著的好处就是解决了空间问题。试想给定我们一个远超计算机内存的数据量让我们找Top K（K在运算能力中），我们怎么办？用前面几个方法有一个隐藏的前提就是：需要计算机能够将数据全部加载到内存。但是很明显不适用于大数据量的情况。
所以在数据量很大的情况下，我们可以通过维护一个大小为K的小顶堆，来完成Top K问题。
我们可以从数组中首先取出 K个元素初始化小顶堆，然后将其余元素与小顶堆堆顶元素对比，如果大于堆顶则替换堆顶，然后刷新堆。等到数组中所有元素遍历完成后，堆中的元素即为所找前K个值。

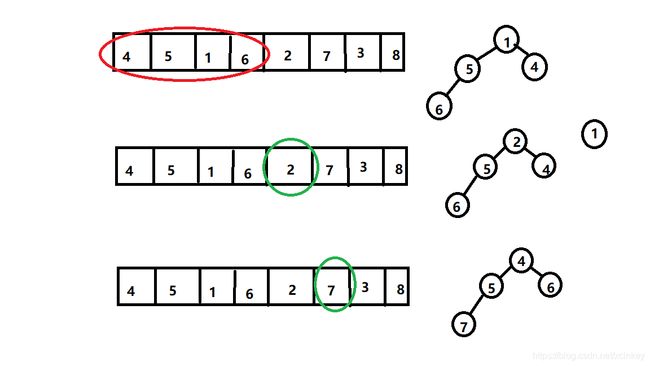
代码如下（示例）：

#include 
#include 
using namespace std;

class BINARYHEAP
{
public:
	BINARYHEAP(void) : mycontainer()
	{
		int t = 0;
		mycontainer.push_back(t);
	}
	~BINARYHEAP(void) {}

	void push(int& val)
	{
		mycontainer.push_back(val);
		int nIndex = mycontainer.size() - 1;

		if (nIndex > 1) {
			int nParentIndex = nIndex / 2;
			while (nIndex != 1) {
				if (mycontainer[nIndex] < mycontainer[nParentIndex]) {
					int temp = mycontainer[nParentIndex];
					mycontainer[nParentIndex] = mycontainer[nIndex];
					mycontainer[nIndex] = temp;
					nIndex = nParentIndex;
					nParentIndex = nIndex / 2;
				}
				else {
					break;
				}
			}
		}
	}
	int size()
	{
		return mycontainer.size()-1;
	}

	int& top()
	{
		return mycontainer[1];
	}

	void pop()
	{
		int nSize = mycontainer.size();
		if (nSize > 2) {
			mycontainer[1] = mycontainer[nSize - 1];
			nSize -= 1;
			int nIndex = 1;
			int nLeftChild = nIndex * 2;
			int nRightChild = nLeftChild + 1;
			int nNext;
			bool bStoped;
			while (nLeftChild < nSize) {
				bStoped = true;
				if (nRightChild >= nSize ||
					mycontainer[nLeftChild] < mycontainer[nRightChild]) {

					if (mycontainer[nLeftChild] < mycontainer[nIndex]) {
						int temp = mycontainer[nLeftChild];
						mycontainer[nLeftChild] = mycontainer[nIndex];
						mycontainer[nIndex] = temp;
						nNext = nLeftChild;
						bStoped = false;
					}
				}
				else {
					int temp = mycontainer[nRightChild];
					mycontainer[nRightChild] = mycontainer[nIndex];
					mycontainer[nIndex] = temp;
					nNext = nRightChild;
					bStoped = false;
				}

				if (bStoped == false) {
					nIndex = nNext;
					nLeftChild = nIndex * 2;
					nRightChild = nLeftChild + 1;
				}
				else {
					break;
				}
			}
		}
		mycontainer.pop_back();
	}

	bool empty()
	{
		return (mycontainer.size() == 1);
	}

	bool refresh(int _Val)
	{
		int nsize = mycontainer.size();
		int nRefreshIndex = -1;
		for (int i = 1; i < nsize; i++) {
			if (mycontainer[i] == _Val) {
				nRefreshIndex = i;
				break;
			}
		}
		if (nRefreshIndex == -1) {
			return false;
		}

		if (_Val < mycontainer[nRefreshIndex]) {
			mycontainer[nRefreshIndex] = _Val;
			int nParentIndex = nRefreshIndex / 2;
			while (nRefreshIndex != 1) {
				if (mycontainer[nRefreshIndex] < mycontainer[nParentIndex]) {
					int temp = mycontainer[nParentIndex];
					mycontainer[nParentIndex] = mycontainer[nRefreshIndex];
					mycontainer[nRefreshIndex] = temp;
					nRefreshIndex = nParentIndex;
					nParentIndex = nRefreshIndex / 2;
				}
				else {
					break;
				}
			}
		}
		else {
			return false;
		}

		return true;
	}
private:
	std::vector<int> mycontainer;
};

int main()
{
	//创建测试用例
	vector<int> v = { 4,5,1,6,2,7,3,8 };
	int k = 4;

	//构建小顶堆
	BINARYHEAP binaryHeap;
	for (int i = 0; i < v.size(); i++)
	{
		if (binaryHeap.size() < k)
		{
			binaryHeap.push(v[i]);
		}
		else
		{
			if (v[i] > binaryHeap.top())
			{
				binaryHeap.push(v[i]);
				binaryHeap.pop();
			}
		}
		
	}

	//输出
	while(!binaryHeap.empty())
	{	
		cout << binaryHeap.top() << endl;
		binaryHeap.pop();
	}

	system("pause");
	return 0;
}

时间复杂度为 O(nlogk)

---

总结

本文旨在整理对于Top K问题的经典解法，其中的重点在于快速选择的方法和利用堆的方法。具体关于小顶堆（优先队列）的构建，后面会专门介绍。