【AI】启发式搜索:贪婪最佳优先搜索与A*原理及python代码实现
搜索算法是利用计算机的高性能来有目的的穷举一个问题的部分或所有的可能情况,从而求出问题的解的一种方法。搜索过程实际上是根据初始条件和扩展规则构造一棵解答树并寻找符合目标状态的节点的过程。
搜索算法的形式化描述:状态、动作、状态转移、路径、测试目标
状态:从原问题转化出的问题描述;
动作:从当前时刻所处状态转移到下一时刻所处状态所进行操作,一般而言这些操作都是离散的;
状态转移:对某一时刻对应状态进行某一种操作后,所能够到达状态;
路径:一个状态序列,该状态序列被一系列操作所连接;
测试目标:评估当前状态是否为所求解的目标状态;
一、问题引入:以寻找最短路径问题为例
问题:寻找从Arad到Bucharest的一条最短路径
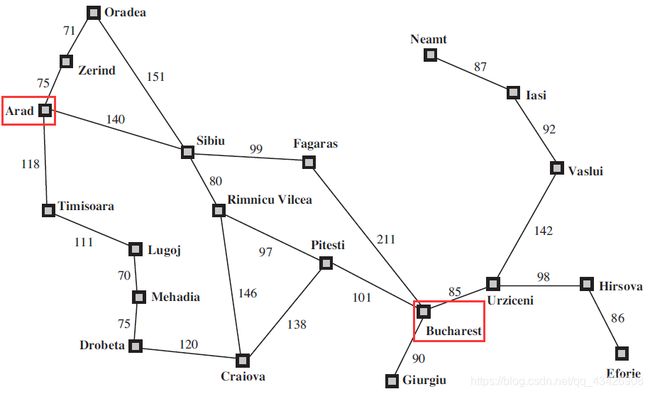
辅助信息:任意一个城市与Bucharest的直线距离

二、启发式搜索(有信息搜索)
在搜索的过程中利用与所求解问题相关的辅助信息,其代表算法为贪婪最佳优先搜索(Greedy best-first search)和A*搜索。
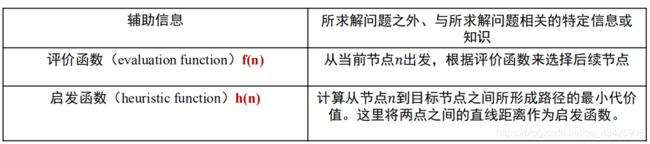
三、贪婪最佳优先搜索及Python实现
1.搜索原理与流程
贪婪最佳优先搜索(Greedy best-first search):评价函数f ()=启发函数ℎ()
在最短路径问题中,启发函数为此刻城市节点到终点城市Bucharest的直线距离,每一次搜索,下一个节点选择与此刻城市连接的所有节点中,与Bucharest的直线距离最短的城市节点。其搜索流程如下:
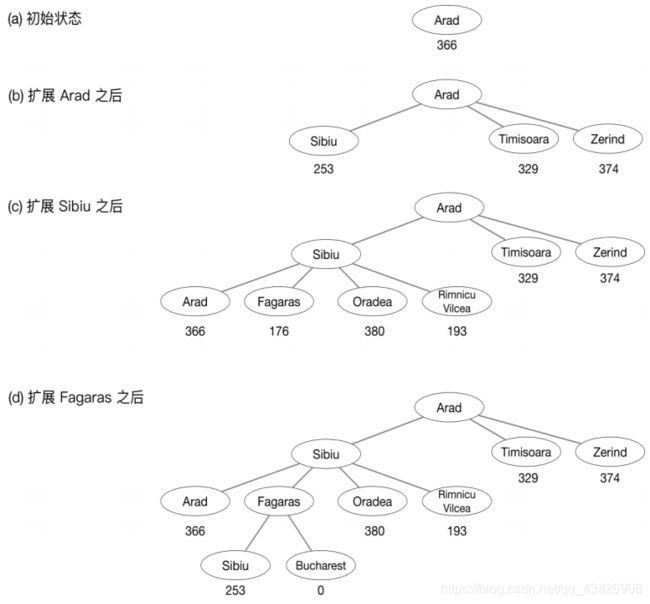
2.Python实现
代码实现为:
import numpy as np
straight_line = {
'Arad':366,
'Bucharest':0,
'Craiova':160,
'Drobeta':242,
'Eforie':161,
'Fagaras':178,
'Giurgiu':77,
'Hirsova':151,
'Iasi':226,
'Lugoj':244,
'Mehadia':241,
'Neamt':234,
'Oradea':380,
'Pitesti':98,
'Rimnicu Vilcea':193,
'Sibiu':253,
'Timisoara':329,
'Urziceni':80,
'Vaslui':199,
'Zerind':374,
}
start = 'Arad'
end = 'Bucharest'
path = [] # 存储最优路线
path.append(start)
distance = [] # 存储最优路线的路线长度
for i in range(20):
path1 = [] # path1中存储该节点的连接城市
distance1 = [] # distance1中存储该节点连接城市的距离
for a in range(len(edges)):
if edges[a][0] == path[-1]:
path1.append(edges[a][1])
distance1.append(edges[a][-1])
# 贪婪最优搜索
min_distance = 1000
for b in range(len(path1)):
if straight_line[path1[b]] < min_distance:
min_distance = straight_line[path1[b]]
temp_distance = distance1[b]
temp_path = path1[b]
path.append(temp_path)
distance.append(temp_distance)
if temp_path == end:
break
X = ' ——> '.join(path)
Y = np.sum(distance)
print('贪婪搜索_最优路线为:', X)
print('贪婪搜索_最优路线长度为:', Y)
运行结果为:
贪婪搜索_最优路线为: Arad ——> Sibiu ——> Fagaras ——> Bucharest
贪婪搜索_最优路线长度为: 450
3.贪婪最佳优先搜索不足之处
(1)贪婪最佳优先搜索不是最优的。经过Sibiu到Fagaras到Bucharest的路径比经过Rimnicu Vilcea到Pitesti到Bucharest的路径要长32公里。
(2)启发函数代价最小化这一目标会对错误的起点比较敏感。考虑从Iasi到Fagaras的问题,由启发式建议须先扩展Neamt,因为其离Fagaras最近,但是这是一条存在死循环路径。
(3)贪婪最佳优先搜索也是不完备的。所谓不完备即它可能沿着一条无限的路径走下去而不回来做其他的选择尝试,因此无法找到最佳路径这一答案。
(4)在最坏的情况下,贪婪最佳优先搜索的时间复杂度和空间复杂度都是O(^),其中是节点的分支因子数目、是搜索空间的最大深度。
四、A*搜索及Python实现
1.搜索原理与流程
A*搜索:评价函数:f () = g() + ℎ()
g() 表示从起始节点到节点的开销代价值;
ℎ() 表示从节点到目标节点路径中所估算的最小开销代价值;
f() 可视为经过节点 、具有最小开销代价值的路径;

在最短路径问题中,g()为当前选择的路径的实际距离,即从上一个节点到下一个节点的实际距离,ℎ()为下一个节点到目标城市的直线距离。每一次搜索,下一个节点选择与此刻城市连接的所有节点中,g()+ℎ()最小的城市节点。其搜索流程如下:

2.Python实现
代码实现为:
import numpy as np
edges=[
('Arad','Zerind',75),
('Arad','Sibiu',140),
('Arad','Timisoara',118),
('Zerind','Oradea',71),
('Oradea','Sibiu',151),
('Timisoara','Lugoj',111),
('Lugoj','Mehadia',70),
('Mehadia','Drobeta',75),
('Drobeta','Craiova',120),
('Sibiu','Fagaras',99),
('Sibiu','Rimnicu Vilcea',80),
('Rimnicu Vilcea','Craiova',146),
('Fagaras','Bucharest',211),
('Rimnicu Vilcea','Pitesti',97),
('Pitesti','Bucharest',101),
('Bucharest','Giurgiu',90),
('Bucharest','Urziceni',85),
('Urziceni','Hirsova',98),
('Urziceni','Vaslui',142),
('Hirsova','Eforie',86),
('Vaslui','Iasi',92),
('Iasi','Neamt',87),
]
straight_line = {
'Arad':366,
'Bucharest':0,
'Craiova':160,
'Drobeta':242,
'Eforie':161,
'Fagaras':178,
'Giurgiu':77,
'Hirsova':151,
'Iasi':226,
'Lugoj':244,
'Mehadia':241,
'Neamt':234,
'Oradea':380,
'Pitesti':98,
'Rimnicu Vilcea':193,
'Sibiu':253,
'Timisoara':329,
'Urziceni':80,
'Vaslui':199,
'Zerind':374,
}
start = 'Arad'
end = 'Bucharest'
path = [] # 存储最优路线
path.append(start)
distance = [] # 存储最优路线的路线长度
for i in range(20):
path1 = [] # path1中存储该节点的连接城市
distance1 = [] # distance1中存储该节点连接城市的距离
for a in range(len(edges)):
if edges[a][0] == path[-1]:
path1.append(edges[a][1])
distance1.append(edges[a][-1])
# A*搜索
fxx = 1000
for b in range(len(path1)):
fxx_min = straight_line[path1[b]] + distance1[b]
if fxx_min < fxx:
fxx = fxx_min
temp_distance = distance1[b]
temp_path = path1[b]
path.append(temp_path)
distance.append(temp_distance)
if temp_path == end:
break
X = ' ——> '.join(path)
Y = np.sum(distance)
print('A*搜索_最优路线为:', X)
print('A*搜索_最优路线长度为:', Y)
运行结果为:
A*搜索_最优路线为: Arad ——> Sibiu ——> Rimnicu Vilcea ——> Pitesti ——> Bucharest
A*搜索_最优路线长度为: 418
3.A*搜索总结
参考资料
中国大学MOOC浙江大学:人工智能
