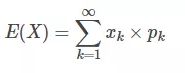概率统计:数学期望、方差、协方差、相关系数、矩
一 、数学期望(均值):
在概率论和统计学中,数学期望(mean)(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和。是最基本的数学特征之一。它反映随机变量平均取值的大小。其公式如下:
xk :表示观察到随机变量X的样本的值。
pk : 表示xk发生的概率。
数学期望反映的是平均水平。通过它,我们能够了解一个群体的平均水平。但另外一个方面,它所包含的信息也是十分有限的,首先是个体信息被压缩了,其次如果单纯看期望的话,是看不出样本的数量。
在概率论和统计学中,数学期望(mean)(或均值,亦简称期望)是试验中每次可能结果的概率乘以其结果的总和
严格的定义如下:
.数学期望的含义: 反映随机变量平均取值的大小
二 、期望、方差、标准差
概率论与数理统计中,最基本概念就是均值、方差、标准差,n个样本xi的集合X。具体公式描述为
对于一维数据的分析,最常见的就是计算平均值(Mean)、方差(Variance)和标准差(Standard Deviation)。
平均值
平均值的概念很简单:所有数据之和除以数据点的个数,以此表示数据集的平均大小;其数学定义为:
在概率论和数理统计中,方差(英文Variance)用来度量随机变量和其数学期望(即均值)之间的偏离程度.方差越大,随机变量的结果越不稳定。常用来评估风险。
方差是各个数据与平均数之差的平方的和的平均数,用字母D表示。
标准差与方差一样,表示的也是数据点的离散程度;其在数学上定义为方差的平方根:
标准差是一组数值自平均值分散开来的程度的一种测量观念。一个较大的标准差,代表一组数据里大部分的数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。
为什么用这么复杂的方法来计算标准差呢,这是因为在实践中,我们发现相当多的数据都呈现近似于“正态分布”
简单的说就是呈现正态分布的一组数据中,靠近中间高点的数字出现的概率要远大于在两侧更远地方出现的概率。
理解正态分布对理解标准差具有重要的意义,回到上面那张钟形曲线图,如果说平均值可以告诉我们这条曲线最高点在什么位置,那么标准差就可以告诉我们这条曲线的宽窄程度。
反过来正态分布也可以用来解释标准差:在一个标准正态分布中,数字出现的概率是固定的。
标准差经常被用来描述数据的波动性,标准差越大说明其偏离均值程度越大,也越罕见,之后回归常态的可能性也在升高。
三 、方差
什么是Variance(方差)
Variance反映的是模型每一次输出结果与模型输出期望之间的误差,即模型的稳定性。反应预测的波动情况。
方差
(variance)是在概率论和统计方差衡量随机变量或一组数据时离散程度的度量。概率论中方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。在许多实际问题中,研究方差即偏离程度有着重要意义。
方差( D(X)或Var(X) )计算公式如下:
X: 表示随机变量。 E(X) : 表示X的期望。 D(X) : 是每个样本值与全体样本值的平均数之差的平方值的平均数
四 、
.标准差是为了描述数据集的波动大小而发明发的。
方差、标准差
方差这一概念的目的是为了表示数据集中数据点的离散程度;其数学定义为:
标准差与方差一样,表示的也是数据点的离散程度;其在数学上定义为方差的平方根:
为什么使用标准差?
与方差相比,使用标准差来表示数据点的离散程度有3个好处:
表示离散程度的数字与样本数据点的数量级一致,更适合对数据样本形成感性认知。依然以上述10个点的CPU使用率数据为例,其方差约为41,而标准差则为6.4;两者相比较,标准差更适合人理解。
表示离散程度的数字单位与样本数据的单位一致,更方便做后续的分析运算。
在样本数据大致符合正态分布的情况下,标准差具有方便估算的特性:66.7%的数据点落在平均值前后1个标准差的范围内、95%的数据点落在平均值前后2个标准差的范围内,而99%的数据点将会落在平均值前后3个标准差的范围内。
(部分转载于) 悦悦_成长日记