数学建模算法与应用（司守奎版）python 代码实现

引言：在准备九月份的华为杯，入门选择了司守奎老师的教材《数学建模算法与应用》，书中仅提供了lingo和matlab的版本，但是python的数据处理能力更加出色，因此考虑在学习的过程中将代码全部用python实现。

第一章：线性规划

基础代码：（例题1.1）

'''
max z = 4x+3y
2x+y <= 10
x+y <= 8
y <= 7
x,y >= 0

'''

#pip install scipy
import numpy as np
from scipy.optimize import linprog

#目标函数
c = np.array([-4,-3])

#约束条件
A = np.array([[2,1],[1,1],[0,1]])
b = np.array([10,8,7])

#边界条件
x_bounds = (0,None)
y_bounds = (0,None)

#求解线性规划问题
res = linprog(c,A_ub=A,b_ub=b,bounds=[x_bounds,y_bounds])

print("Optimal value:", -res.fun)
print("Optimal value:",res.x)

基础代码：（例题1.2）

'''
max w = 2x+3y-5z
x+y+z = 7
2x-5y+z >= 10
x+3y+z <= 12
x,y,z >= 0

'''

#pip install scipy
import numpy as np
from scipy.optimize import linprog

#目标函数
c = np.array([-2,-3,5])

#约束条件
A = np.array([[-2,5,-1],[1,3,1]])
b = np.array([-10,12])

A_ = np.array([[1,1,1]])
b_ = np.array([7])

#边界条件
x_bounds = (0,None)
y_bounds = (0,None)
z_bounds = (0,None)

#求解线性规划问题
res = linprog(c,A_ub=A,b_ub=b,A_eq=A_,b_eq=b_,bounds=[x_bounds,y_bounds,z_bounds])

print("Optimal value:", -res.fun)
print("Optimal value:",res.x)

基础代码：（例题1.3）

'''
min w = 2x+3y+z
x+4y+2z >= 8
3x+2y >= 6
x,y,z >= 0

'''

#pip install scipy
import numpy as np
from scipy.optimize import linprog

#目标函数
c = np.array([2,3,1])

#约束条件
A = np.array([[-1,-4,-2],[-3,-2,0]])
b = np.array([-8,-6])

#边界条件
x_bounds = (0,None)
y_bounds = (0,None)
z_bounds = (0,None)

#求解线性规划问题
res = linprog(c,A_ub=A,b_ub=b,bounds=[x_bounds,y_bounds,z_bounds])

print("Optimal value:", res.fun)
print("Optimal value:",res.x)

基础代码：（例题1.5）

#pip install scipy
import numpy as np
from scipy.optimize import linprog

#目标函数
c = np.array([1,1,2,2,3,3,4,4])

#约束条件
A = np.array([[1,-1,-1,1,-1,1,1,-1],[1,-1,-1,1,1,-1,-3,3],[1,-1,-1,1,-2,2,3,-3]])
b = np.array([-2,-1,-1/2])

#边界条件
u1_bounds = (0,None)
u2_bounds = (0,None)
u3_bounds = (0,None)
u4_bounds = (0,None)
v1_bounds = (0,None)
v2_bounds = (0,None)
v3_bounds = (0,None)
v4_bounds = (0,None)

#求解线性规划问题
res = linprog(c,A_ub=A,b_ub=b,bounds=[u1_bounds,v1_bounds,u2_bounds,v2_bounds,u3_bounds,v3_bounds,u4_bounds,v4_bounds])

print("Optimal value:", res.fun)
print("Optimal value:",res.x)

基础代码：（投资的收益与风险----------------模型一）

'''
模型一：固定风险水平 优化收益
'''

#pip install scipy
import numpy as np
from scipy.optimize import linprog
import matplotlib.pyplot as plt

def model(a):
    #目标函数
    c = np.array([-(0.05),-(0.28-0.01),-(0.21-0.02),-(0.23-0.045),-(0.25-0.065)])

    #约束条件
    A = np.array([[0,0.025,0,0,0],[0,0,0.015,0,0],[0,0,0,0.055,0],[0,0,0,0,0.026]])
    b = np.array([a,a,a,a])

    A_ = np.array([[(1),(1+0.01),(1+0.02),(1+0.045),(1+0.065)]])
    b_ = np.array([1])

    #边界条件
    x1_bounds = (0,None)
    x2_bounds = (0,None)
    x3_bounds = (0,None)
    x4_bounds = (0,None)
    x5_bounds = (0,None)

    #求解线性规划问题
    res = linprog(c,A_ub=A,b_ub=b,A_eq =A_,b_eq=b_,bounds=[x1_bounds,x2_bounds,x3_bounds,x4_bounds,x5_bounds])

    # print("Optimal value:",-res.fun)
    # print("Optimal value:",res.x)

    return -res.fun

def draw(x,y):
    # 绘图
    x = x
    y = y
    plt.plot(x, y)  # 绘制x和y的函数关系图
    plt.xlabel('a')  # x轴标签
    plt.ylabel('Q')  # y轴标签
    plt.title('风险与收益的关系图',fontproperties='SimHei')  # 图表标题
    plt.show()  # 显示图表


if __name__ == '__main__':
    a = 0;
    x = [0];
    y = [0];
    while a < 0.05:
        y_res = model(a)
        a = a+0.001
        x.append(a)
        y.append(y_res)

    draw(x,y)

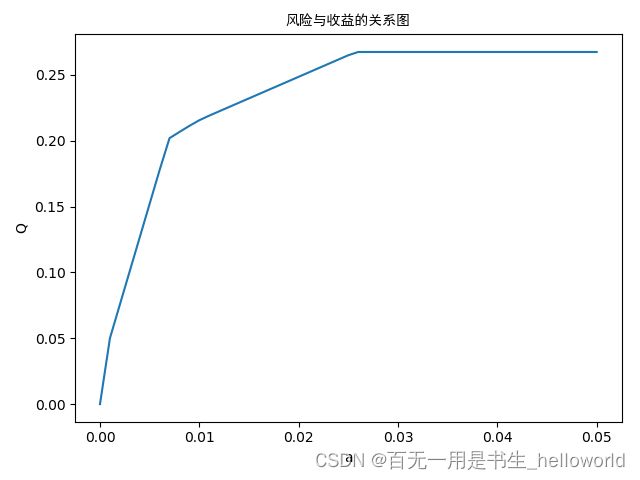
• 思考：虽然根据关系图可以确定转折点的大致范围，但是怎么确定这个具体值是多少是个问题哎？而且步长为0.001，终止条件为0.05也是根据经验设定的吧，在开始的时候如果没有设定好【巧合值】的话可能连转折点都很难发现。