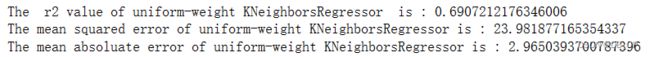监督学习---K近邻

  机器学习中监督学习模型的任务重点在于根据已有经验知识对未知样本的目标/标记进行预测。根据目标预测变量的类型不同，把监督学习任务大体分为分类学习和回归预测两类。分类学习是最为常见的监督学习问题，其中，最基础的是二分类问题，除此之外还有多分类问题。

一、K近邻算法原理

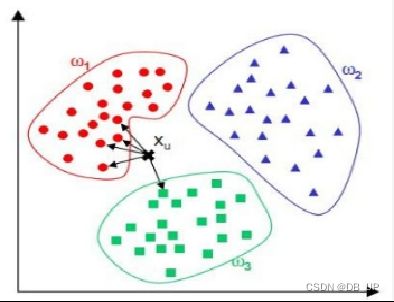
  存在一个样本数据集合，也称作训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每个数据与所属分类的对应关系。输入没有标签的新数据后，将新数据的每个特征与样本集中数据对应的特征进行比较，然后算法提取样本集中特征最相似数据（最近邻）的分类标签。一般来说，只选择样本数据集中前N个最相似的数据。K一般不大于20，最后，选择k个中出现次数最多的分类，作为新数据的分类。换句话说计算待分类物体与其他物体之间的距离；统计距离最近的K个邻居；对于K个最近的邻居，它们属于哪个分类最多，待分类物体就属于哪一类。

二、距离计算

三、K值选择

  如果选择较小的K值，“学习”的近似误差（approximation error)会减小，但 “学习”的估计误差（estimation error) 会增大，噪声敏感，
K值的减小就意味着整体模型变得复杂，容易发生过拟合。

  如果选择较大的K值，减少学习的估计误差，但缺点是学习的近似误差会增大。K值的增大就意味着整体的模型变得简单。

四、损失函数

  其中I为指示函数,当yi=cj时I为1，否则I为0。要使误分类率最小，即经验风险最小，就要使I最大，所以多数表决规则等价于经验风险最小化。

五、线性分类器–K近邻分类

#k近邻分类
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split #用于分割数据集
from sklearn.preprocessing import StandardScaler     # 归一化
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import classification_report
iris=load_iris()
iris.data.shape
#鸢尾花数据集有150朵数据样本，并且均匀分布在3个不同的亚种，每个数据样本被4个不同的花瓣、花萼的形状特征所描述
#输出（150，4）
x=iris.data
y=iris.target
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.3,random_state=33)
ss=StandardScaler()
X_train=ss.fit_transform(x_train)
X_test=ss.transform(x_test)
knc=KNeighborsClassifier()
knc.fit(X_train,y_train)
knc_y_predict=knc.predict(X_test)
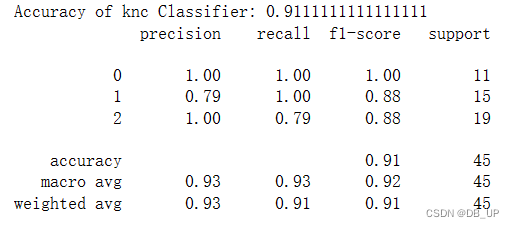
print('Accuracy of knc Classifier:',knc.score(X_test,y_test))
print(classification_report(y_test,knc_y_predict))

KNeighborsClassifier(n_neighbors=5,weights='uniform',algorithm='auto',leaf_size=30,p=2,metric='minkowski',metric_params=None,n_jobs=1,**kwargs)
n_neighbors: 即为K值的选择；K取值较小时，模型复杂度高，训练误差会减小，泛化能力减弱；K取值较大时，模型复杂度低，训练误差会增大，泛化能力有一定的提高。因此，K值选择应适中，K值一般小于20。
metric: 距离度量KNN算法用距离来度量两个样本间的相似度。常用的距离表示方法：欧式距离、曼哈顿距离、余弦距离等。
weights: 'uniform' : 统一的权重;'distance': 权重点等于他们距离的倒数。使用此函数，更近的邻居对于所预测的点的影响更大。
algorithm:计算最近邻居用的算法。
	'ball_tree' 是为了克服kd树高纬失效而发明的，其构造过程是以质心C和半径r分割样本空间，每个节点是一个超球体。
	'kd_tree' 构造kd树存储数据以便对其进行快速检索的树形数据结构，kd树也就是数据结构中的二叉树。以中值切分构造的树，每个结点是一个超矩形，在维数小于20时效率高。
	'brute' 使用暴力搜索.也就是线性扫描，当训练集很大时，计算非常耗时
	'auto' 会基于传入fit方法的内容，选择最合适的算法。
leaf_size:传入BallTree或者KDTree算法的叶子数量。
p:用于Minkowski metric（闵可夫斯基空间）的超参数。p = 1, 相当于使用曼哈顿距离 (l1)，p = 2, 相当于使用欧几里得距离(l2) 对于任何 p ，使用的是闵可夫斯基空间(l_p)
n_jobs:用于搜索邻居的，可并行运行的任务数量。如果为-1, 任务数量设置为CPU核的数量。不会影响fit方法。

  k近邻分类器对45条鸢尾花测试样本分类的准确性为91%，平均精确率、召回率、F1指标分别为0.93、0.91、0.91。

六、线性回归器–K近邻回归

from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import r2_score,mean_absolute_error,mean_squared_error
#初始化k近邻回归器，并且调整配置，使得预测的方式为平均回归，weights='uniform'
boston = pd.read_excel('boston_house_price.xlsx')
#使用线性核函数配置的支持向量机进行回归训练，并对测试样本进行预测
x=np.array(boston.iloc[:,:-1])
y=np.array(boston.iloc[:,-1])
x_train,x_test,y_train,y_test = train_test_split(x,y,test_size=0.25,random_state=33)
ss_x=StandardScaler()
x_train=ss_x.fit_transform(x_train)
x_test=ss_x.transform(x_test)
##说明一下：fit_transform与transform都要求操作2D数据，而此时的y_train与y_test都是1D的，因此需要调用reshape(-1,1)，例如：[1,2,3]变成[[1],[2],[3]]
ss_y=StandardScaler()
y_train=ss_y.fit_transform(y_train.reshape(-1,1))
y_test=ss_y.transform(y_test.reshape(-1,1))

uni_knr=KNeighborsRegressor(weights='uniform')
uni_knr.fit(x_train,y_train)
uni_knr_y_predict=uni_knr.predict(x_test)
#初始化k近邻回归器，并且调整配置，使得预测的方式根据距离加权回归，weights='distance'
dis_knr=KNeighborsRegressor(weights='distance')
dis_knr.fit(x_train,y_train)
dis_knr_y_predict=dis_knr.predict(x_test)

print('The  r2 value of uniform-weight KNeighborsRegressor  is :',uni_knr.score(x_test,y_test))
print('The mean squared error of uniform-weight KNeighborsRegressor is :',mean_squared_error(ss_y.inverse_transform(y_test),ss_y.inverse_transform(uni_knr_y_predict)))
print('The mean absoluate error of uniform-weight KNeighborsRegressor is :',mean_absolute_error(ss_y.inverse_transform(y_test),ss_y.inverse_transform(uni_knr_y_predict)))

print('The  r2 value of distance-weight KNeighborsRegressor  is :',dis_knr.score(x_test,y_test))
print('The mean squared error of distance-weight KNeighborsRegressor is :',mean_squared_error(ss_y.inverse_transform(y_test),ss_y.inverse_transform(dis_knr_y_predict)))
print('The mean absoluate error of distance-weight KNeighborsRegressor is :',mean_absolute_error(ss_y.inverse_transform(y_test),ss_y.inverse_transform(dis_knr_y_predict)))

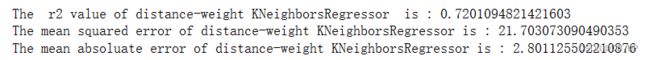
  K近邻分类与K近邻回归一样，均属于无参数模型。通过多数表决方式进行预测，k值选择、距离度量、分类决策规则是K近邻法的三要素。

七、K近邻算法优缺点

1、优点

精度高
对异常值不敏感
无数据输入假定

2、缺点

计算复杂度高
空间复杂度高

3、适用数据范围

数值型和标称型