5.5 数据结构——二叉树的遍历
5.5.1 二叉树遍历的定义
顺着某一条搜索路径巡访二叉树中的结点,使得每个结点均被访问一次,而且仅被访问一次(又称周游)。
遍历目的:得到树中所有结点的一个线性排列。
遍历用途:它是树结构插入、删除、修改、查找和排序运算的前提,是二叉树一切运算的基础和核心。
5.5.2 二叉树遍历的方法
假设:L是遍历左子树,D是访问根结点,R是遍历右子树,那么遍历整个二叉树的方案有:
DLR、LDR、LRD、DRL、RDL、RLD六种。
如果规定先左后右,则只有前三种:
DLR——先(根)序遍历
LDR——中(根)序遍历
LRD——后(根)序遍历
先序遍历:若二叉树为空,则空操作,否则先访问根结点,再先序遍历左子树,然后先序遍历右子树。
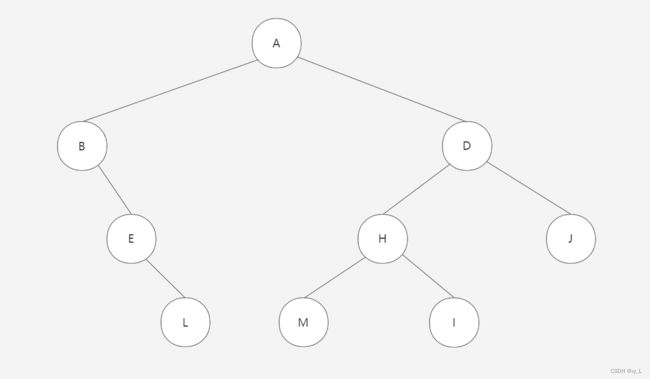
上图的二叉树的先序遍历序列是:ABELDHMIJ
中序遍历:若二叉树为空,则空操作,否则先中序遍历左子树,再访问根结点,然后中序遍历右子树。
上图的二叉树的中序遍历序列是:BELAMHIDJ
后序遍历:若二叉树为空,则空操作,否则先进行后序遍历左子树,然后再后序遍历右子树,最后再访问根结点。
上图的二叉树的后序遍历序列是:LEBMIHJDA
还有一种层序遍历:若树为空,则空操作,否则从树的第一层,也就是根结点开始访问,从上而下逐层遍历,在同一层中,按从左到右的顺序对结点逐个访问。
上图中的二叉树的层次遍历序列是:ABDEHJLMI
5.5.3 根据遍历序列确定二叉树
若二叉树中各结点的值均不相同,则二叉树结点的先序遍历、中序遍历和后序遍历序列都是唯一的。
由二叉树的先序序列和中序序列,或由二叉树的后序序列和中序序列可以确定唯一一棵二叉树。
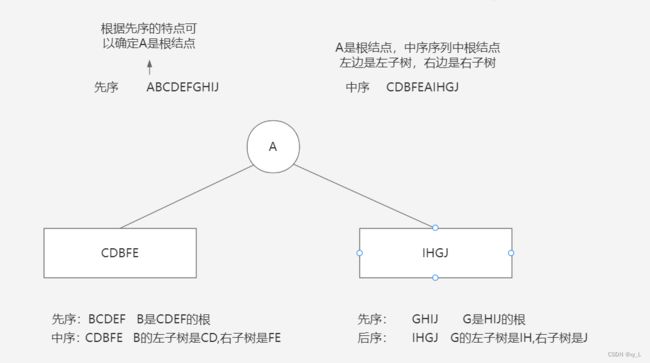
由先序序列和中序序列确定二叉树:
先序序列:ABCDEFGHIJ
中序序列:CDBFEAIHGJ
由后序序列和先序序列确定二叉树:
中序序列:BDCEAFHG
有序序列:DECBHGFA
5.5.4 二叉树的遍历算法
1、先序遍历:
Status PreOrderTraverse(BiTree T)
{
if (T == NULL)
return false;
else
{
visit(T);
PreOrderTraverse(T->lchild);
PreOrderTraverse(T->rchild);
}
return true;
}2、中序遍历:
Status InOrderTraverse(BiTree T)
{
if (T == NULL)
return false;
else
{
InOrderTraverse(T->lchild);
visit(T);
InOrderTraverse(T->rchild);
}
return true;
}3、后序遍历:
Status PostOrderTraverse(BiTree T)
{
if (T == NULL)
return false;
else
{
PostOrderTraverse(T->lchild);
PostOrderTraverse(T->rchild);
visit(T);
}
return true;
}4、中序遍历非递归算法:
二叉树中序遍历的非递归算法的关键是在中序遍历过某结点的整个左子树后,如何找到该结点的根以及右子树。
基本思想:
(1)建立一个栈
(2)根结点进栈,遍历左子树
(3)根结点出栈,输出根结点,遍历右子树
Status InOrderTraverse(BiTree T)
{
BiTree p, q;
SqStack S;
InitStack(&S);
while (p || !StackEmpty(S))
{
if (p)
{
Push(&S, p);
p = p->lchild;
}
else
{
Pop(S, q);
printf("%c", q->data);
p = q->rchild;
}
}
return true;
}5、层序遍历:
算法设计思路,使用一个队列:
(1)将根结点入队;
(2)队不空是循环,从队列中出队一个结点,访问它;
(3)若出队的结点:
①有左孩子结点,将左孩子入队
②有右孩子结点,将右孩子入队
void LevelOrder(BTNode *B)
{
BTNode *P;
SqQueue *qu;
InitQueue(qu);
EnQueue(qu, B);
while (!QueueEmpty(qu))
{
deQueue(qu, p);
printf("%c", p->data);
if (p->lchild != NULL)
EnQueue(qu, p->lchild);
if (p->rchild != NULL)
EnQueue(qu, p->rchild);
}
}