算法通关村第13关【白银】| 数字与数学高频问题
数组实现加法
1.加一
思路:不进位末尾加一,进位挨个加一
99,999...进位,新建长度+1的数组,res[0]=1,直接返回
lass Solution {
public int[] plusOne(int[] digits) {
for(int i = digits.length-1;i>=0;i--){
int num = ++digits[i];
if(num<10){
return digits;
}else{
digits[i] = num % 10;
}
}
int[] res = new int[digits.length + 1];
res[0] = 1;
return res;
}
}2.字符串相加
思路:从尾部加起,记录进位/10,本位%10,位数不一样0补齐
class Solution {
public String addStrings(String num1, String num2) {
char[] s1 = num1.toCharArray();
char[] s2 = num2.toCharArray();
StringBuilder sb = new StringBuilder();
int len1 = s1.length-1;
int len2 = s2.length-1;
int carry = 0;
while(carry != 0 || len1>=0||len2>=0){
int n1 = 0;
int n2 = 0;
if(len1>=0&&len2>=0){
n1 = s1[len1] - '0';
n2 = s2[len2] - '0';
}
else if(len2<0&&len1<0){
n1 = 0;
n2 = 0;
}
else if(len1<0){
n2 = s2[len2] - '0';
n1=0;
}
else if(len2<0){
n1 = s1[len1] - '0';
n2=0;
}
int num = n1+n2+carry;
if(num>=10){
sb.append(num%10);
carry = num/10;
}else{
sb.append(num);
carry = 0;
}
len1--;
len2--;
}
return sb.reverse().toString();
}
}3.二进制加法
思路:和十进制加法一样,逢二进一/2,本位取模%2,位数不一样0补齐
class Solution {
public String addBinary(String a, String b) {
StringBuilder sb = new StringBuilder();
int carry = 0;
int len1 = a.length();
int len2 = b.length();
for(int i = len1 - 1,j = len2 - 1;(i>=0||j>=0||carry!=0);i--,j--){
int n1 = i >= 0? a.charAt(i) - '0' : 0;
int n2 = j >= 0? b.charAt(j) - '0' : 0;
int n = n1 + n2 + carry;
if(n>=2){
sb.append(n%2);
carry = n/2;
}else{
sb.append(n);
carry = 0;
}
}
return sb.reverse().toString();
}
}幂运算
1.2的幂
思路:每次除2直到除到底是不是能除尽,也就是2的n次方等于n。
class Solution {
public boolean isPowerOfTwo(int n) {
if(n%2!=0&&n!=1||n==0){
return false;
}
while(n%2==0){
n = n >> 1;
}
if(n!=1){
return false;
}else{
return true;
}
}
}解法二:位运算,2的n次方说明首位为1其他位都是0,通过n&(n-1)将末尾1变0 比较是否为0
public static boolean isPowerOfTwo2(int n) {
return n > 0 && (n & (n - 1)) == 0;
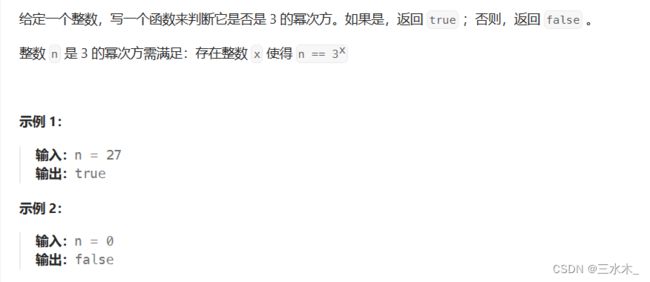
}2.3的幂
思路:同上一题,2变成3
class Solution {
public boolean isPowerOfThree(int n) {
if(n%2==0||n<=0){
return false;
}
while(n%3==0){
n /= 3;
}
return n == 1;
}
}解法二:位运算,int范围内3的最高幂次数是3的19次方1162261467,只需要去除n能除整就是
public static boolean isPowerOfThree2(int n) {
return n > 0 && 1162261467 % n == 0;
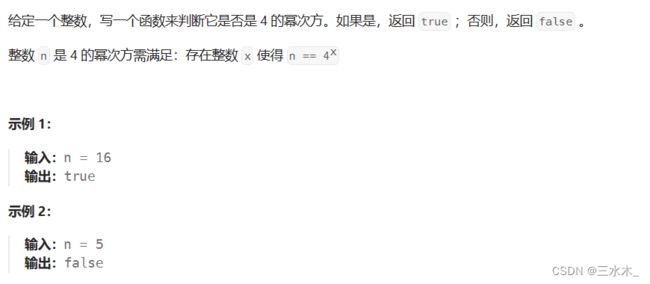
}3.4的幂
class Solution {
public boolean isPowerOfFour(int n) {
if(n == 1){
return true;
}
if(n%2!=0||n<=0){
return false;
}
while(n%4 == 0){
n /= 4;
}
return n == 1;
}
}解法二:位运算,4(2^2)的n次方说明首位为1其他位都是0,同时它还是2的n次方,特别的首位1处在奇数位置上,例如:100、10000,通过n&(n-1)将末尾1变0 比较是否首位为1其他位为0,再然后判断1是不是在奇数位置上,也就是&偶数位全是1奇数为全是0,如果偶数位为1就false
class Solution {
public boolean isPowerOfFour(int n) {
return n > 0 && (n & (n - 1)) == 0 && (n & 0xaaaaaaaa) == 0;
}
}
4.幂函数
思路:快速幂,折半乘
快速幂+递归,遇到奇数*x
class Solution {
public double myPow(double x, int n) {
if(x==1||n==0){
return 1.0;
}
if(x == 0){
return 0.0;
}
long N = n;
return n>0 ? quickMul(x,N) : 1.0/quickMul(x,-N);
}
public double quickMul(double x,long n){
if(n == 0){
return 1.0;
}
double res = quickMul(x,n/2);
if(n%2==1){
return res*res*x;
}else{
return res*res;
}
}
}快速幂+迭代
13的二进制为1101,15的二进制为1111
3^13=3^8*3^4*3^0*3^1
再如3^15 = 3^8*3^4*3^2*3^1
进行幂次方拆分,从低位1开始每循环右移一次就x平方一次,遇见1结果就*x
class Solution {
public double myPow(double x, int n) {
if(x==1||n==0){
return 1.0;
}
if(x == 0){
return 0.0;
}
long N = n;
if(n<0){
N = -N;
}
double res = 1.0;
while(N>0){
if((N & 1) == 1){
res = res*x;
}
x *= x;
N = N/2;
}
return n<0 ? 1.0/res : res;
}
}