C++:AVL树
目录
一、关于AVL树
二、AVL树的注意事项
1、平衡因子的更新规则:
2、旋转的处理
①、右右:左单旋
②、左左:右单旋
③、左右:先左单旋再右单旋
④、右左:先右单旋再左单旋
三、AVL树模拟实现
一、关于AVL树
前面学过二叉搜索树,数据在有序或是接近有序时,二叉搜索树效率就非常低了,因此这里引入了AVL树,又叫高度平衡二叉搜索树
AVL树是以人名命名的,是两位俄罗斯的数学家提出的,所以取他们名字的缩写命名
他们提出的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度差不超过1(需要对树中的结点进行调整),就可以保证效率
那这里为什么不保证左右高度相等,这样不是效率更高吗?答案是做不到,比如只有两个结点,一个是根结点,怎么能做到左右字树高度相等呢,肯定做不到,所以才要求保证左右子树高度差不超过1
AVL树要求:
1、它的任何一个子树左右高度差都不超过1/2、左右字树的高度差(平衡因子)的绝对值不超过1(-1/0/1)
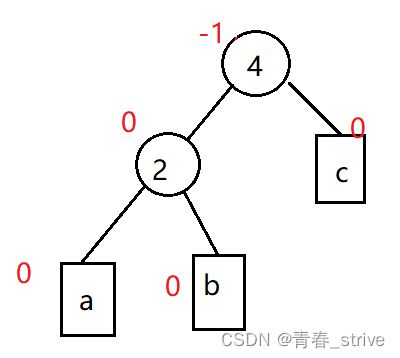
平衡因子:右子树高度 - 左子树高度,平衡因子是标在每个结点旁的,第2条平衡因子是非必须的,即可以使用也可以不用,我们下面的模拟实现时会用平衡因子
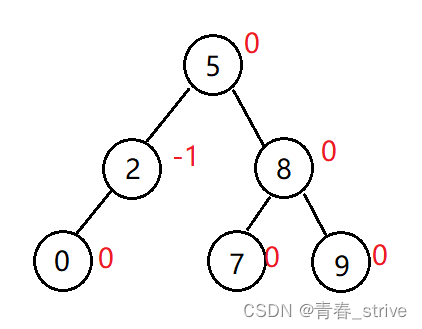
如图,红数字即平衡因子:
二、AVL树的注意事项
在我们插入时,首先和搜索二叉树一样,先找到插入结点该插入的位置,然后要注意AVL树中各个结点的链接关系,还要注意插入后的平衡因子的更新进行分类讨论
1、平衡因子的更新规则:
①新增结点在右,parent->_bf++;新增结点在左,parent->_bf--
②更新后,parent->_bf == 1 or -1,则说明插入前parent的平衡因子是0,说明插入前的左右字树高度相同,插入后有一边高了,parent的子树高度变了,所以需要继续往上更新
③更新后,parent->_bf == 0,则说明插入前parent的平衡因子是1 or -1,说明插入前的左右字树一边高一边低,插入后高度相同了,即插入到了低的那一边子树上了,parent的子树高度没变,所以不需要继续往上更新
④更新后,parent->_bf == 2 or -2,则说明插入前parent的平衡因子是1 or -1,说明插入前的左右字树一边高一边低,已经是临界值了,插入到了高的那一边子树上了,打破了平衡,不满足AVL树的规则,parent所在的子树需要做旋转处理
⑤更新后,parent->_bf > 2 or < -2,是不可能出现这种情况的,如果出现,就说明插入前就不是AVL树,需要检查前面的操作
下面演示插入结点平衡因子的更新情况:红圈表示插入的结点
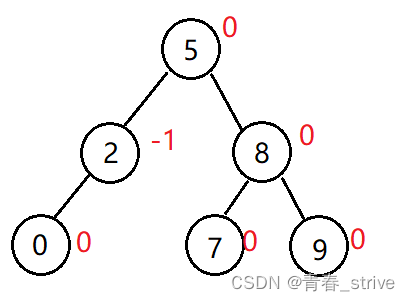
首先AVL树是这样的:
接着右子树插入一个结点,斜线就表示平衡因子的改变
在刚刚插入结点的左边插入:
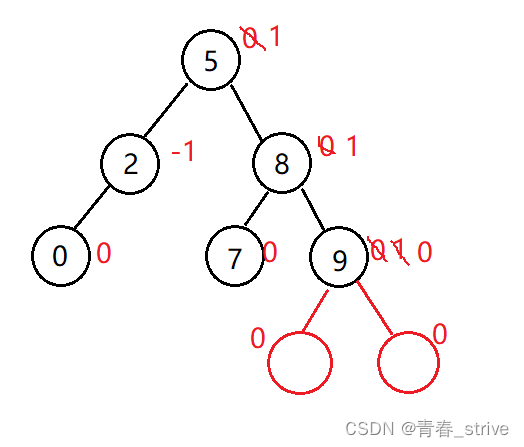
在刚刚插入结点的子树插入:
到这里,可以发现结点8的平衡因子为2,这时不符合AVL树的规则,所以需要旋转处理
2、旋转的处理
旋转的原则:
①、旋转后变为平衡树
②、保持二叉搜索树规则
旋转具体的情况图:
红圈表示插入的结点
①、右右:左单旋
右右指:新结点插入较高右子树的右侧
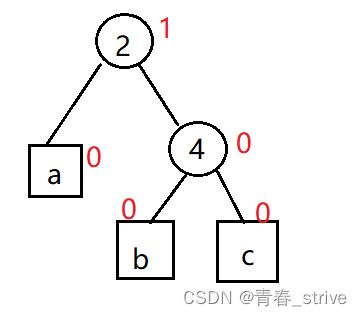
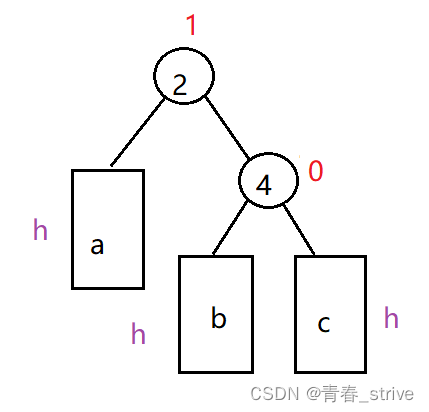
具体子树类型太多,无法一一列举,所以给出模型图代替所有可能出现的情况:a、b、c表示h>=0的平衡树,b可能存在也可能不存在(在模拟实现时需要讨论是否存在的情况,因为只有b需要改变链接关系);
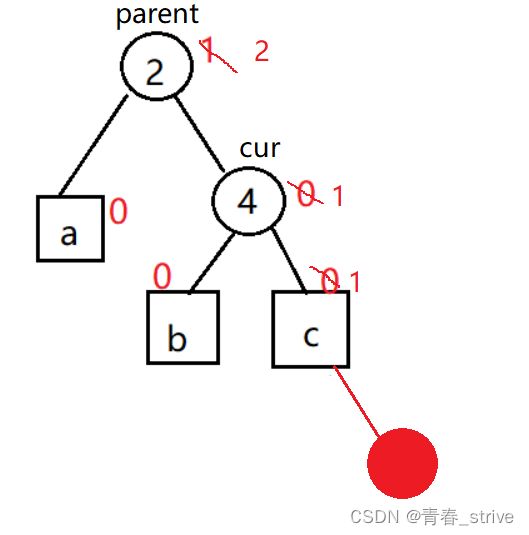
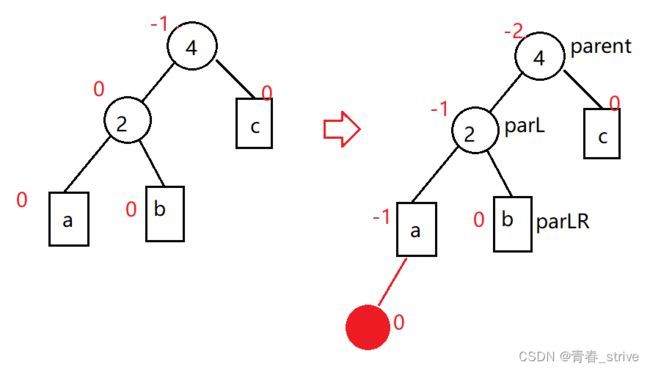
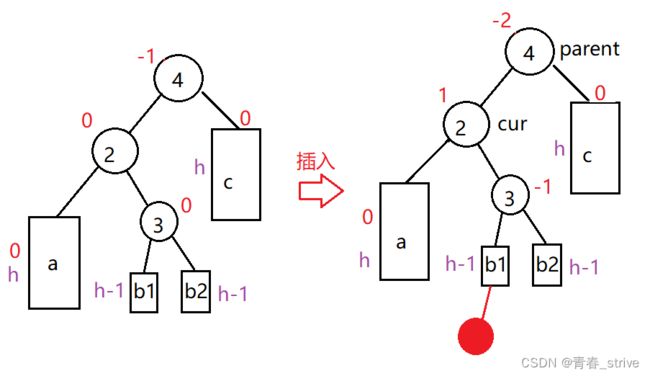
插入后parent->_bf == 2 && cur->_bf == 1,如下图所示:
如果插入结点插入到c子树下,则结点2的平衡因子会变为2,这时的处理方法为:将4作为根结点,2及2的子树a作为4的左子树,并将4原来的左子树b作为2的右子树
能这样做的理由也很简单,4的左子树b一定比2大,所以可以作为2的右子树,而结点2及2的左子树a一定比4小,所以也可以整体放在4的左边,作为左子树
在实现左单旋的代码时,需要将他们旋转后做出改变的_parent、_left、_right一一对应上,其次还有两种情况,平衡因子为2的parent结点,到底是整棵树的根结点还是子树的根结点,对应下面两个图:
第一种:平衡因子为2的结点是整棵树的根结点,这时只需要将改变后的根结点的_parent指向nullptr即可
第二种:平衡因子为2的结点是子树的根结点,这时则需要将改变后子树的根结点链接上_parent
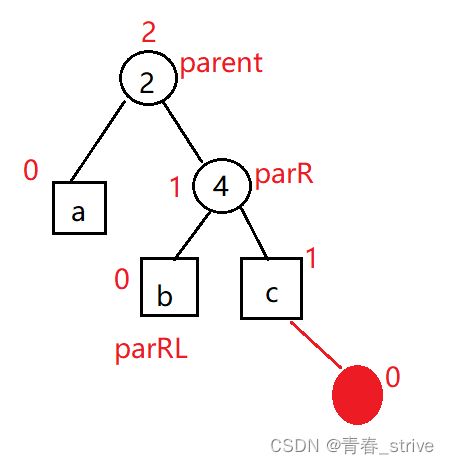
这里根结点是结点2,但是平衡因子为2的结点却是结点4,不是根结点,即第二种情况
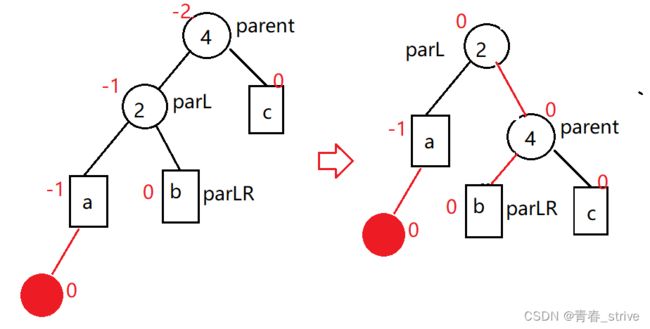
代码中的parent就是平衡因子为2的结点 ,其中parR、parRL就是需要改变的结点的名字,当然parRL可能不存在,各结点名称如下图所示位置:
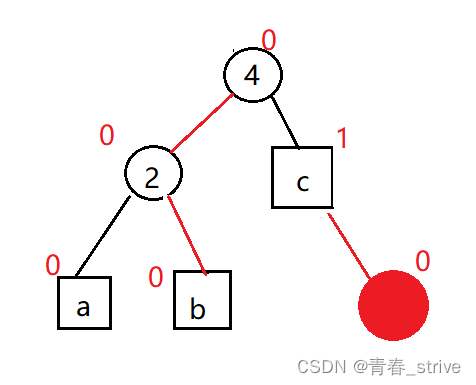
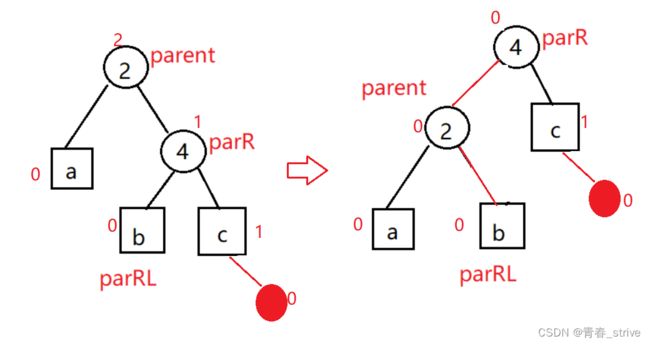
改变后为下图:
最终parent和parR的平衡因子都变为了0
具体代码实现在下方模拟实现中的RotateL函数中
②、左左:右单旋
左左指:新结点插入较高左子树的左侧
右旋和上面的左旋一样,具体子树类型太多,无法一一列举,所以给出模型图代替所有可能出现的情况:a、b、c表示h>=0的AVL子树,可能存在也可能不存在(在模拟实现时需要讨论是否存在的情况);
插入后parent->_bf == -2 && parL->_bf == -1,如下图所示:
图中 ,在模拟实现的代码中会体现
这时的改变方法就是:将结点4及结点4的子树c作为结点2的右子树,将原本结点2的右子树b作为结点4的左子树
因为结点4本身就大于结点2,所以可以做结点2的右子树,而结点2及结点2的所有子树都小于结点4,所以2的右子树做可以作为4的左子树
改变后如下图所示:
同样,最终parent和parL的平衡因子都变为了0
这里也有两种情况,平衡因子为-2的parent结点,到底是整棵树的根结点还是子树的根结点,对应下面两个图:
第一种:平衡因子为-2的结点是整棵树的根结点,这时只需要将改变后的根结点的_parent指向nullptr即可
第二种:平衡因子为-2的结点是子树的根结点,这时则需要将改变后子树的根结点链接上_parent
这里根结点是结点2,但是平衡因子为2的结点却是4,不是根结点
最终代码实现也在下面的模拟实现中
③、左右:先左单旋再右单旋
左右指:新结点插入较高左子树的右侧
具体情况无法一一列举,所以还是以模型图举例说明:
第一种情况:a,b,c的高度都为0,即a/b/c都不存在:
由于左右是指新结点插入较高左子树的右侧,那么如果a,b,c子树都存在,就相当于插入到b子树的下面,这时就有两种情况需要讨论,即插入到b的左还是b的右
那么这时上面的模型图无法准确表示,因为上面的图b表示的就是一整个子树,也包括了插入的部分,所以模型图做以改进:
左图变为右图,将b分为了结点3和结点3的左右字树b1和b2,这样在接下来的插入中,可以清楚地看到插入到b1还是b2,更好的分情况讨论,并且如果a子树的高度是h,那么b1、b2子树的高度是h-1,因为多分了结点3出来,下图中用紫色明确标注出来了
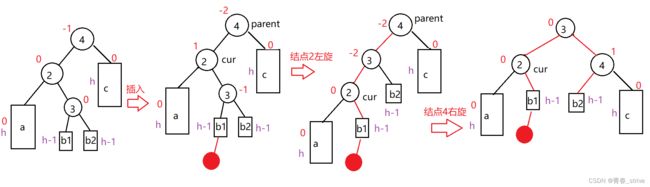
第二种情况:新结点插入到b的左侧,即b1:
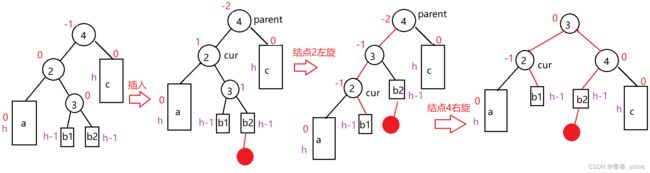
第三种情况:新结点插入到b的右侧,即b2:
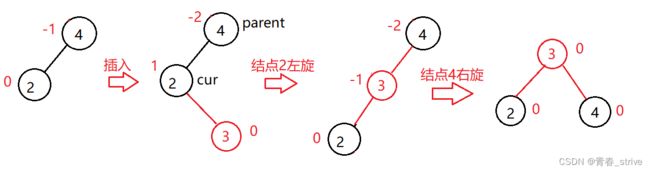
而通过双旋后的结果,我们也可以得出双旋的方法:
将结点3位置的左右字树分别给了结点parent和cur,然后结点3做根结点,结点2、4做它的左右字树
这里也就不说左旋右旋的依据了,参考上面的左单旋右单旋,同样代码实现旋转也很简单,复用一下左单旋右单旋即可,主要是处理三种不同情况的平衡因子
而区分这三种情况,主要是通过插入后parLR位置的平衡因子
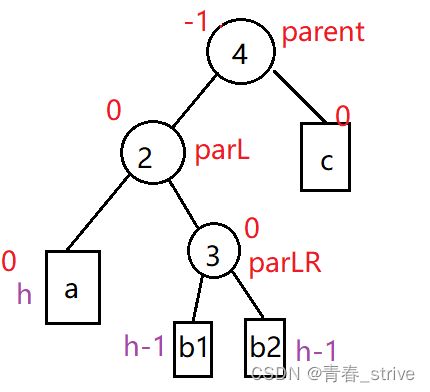
因此旋转前的位置需要记录一下,即parent、parL、parLR位置如下图所示:
第一种情况,parLR位置就是插入的结点,所以平衡因子是0
第二种情况,插入在b1下,所以parLR平衡因子是-1
第三种情况,插入在b2下,所以parLR平衡因子是1
而不管怎么旋转,只有parent、parL、parLR这三个位置的平衡因子变了,所以代码只需要改这三个位置的平衡因子
④、右左:先右单旋再左单旋
左右指:新结点插入较高右子树的左侧
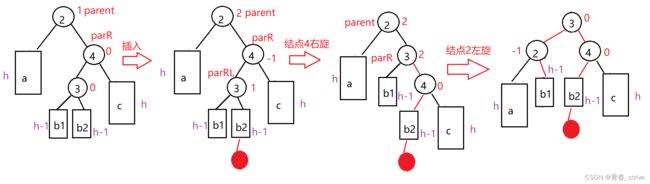
同样给出模型图,如下:其中紫色标注的是a、b、c的高度h,h >= 0
第一种情况:a,b,c的高度都为0,即a/b/c都不存在:
同样由于无法准确表示b存在时,插入到b的左侧还是b的右侧的情景,所以模型图做以改进:
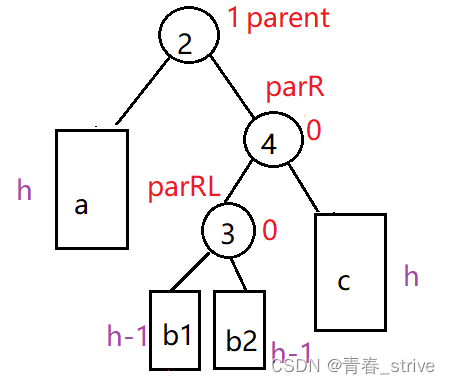
h表示abc子树的高度,parent、parR、parRL是三个位置
第二种情况:新结点插入到b的左侧,即b1
第三种情况:新结点插入到b的右侧,即b2
这三种不同情况的旋转同样复用签的代码即可,主要是平衡因子的改变:
而区分这三种情况,主要是通过插入后parRL位置的平衡因子
因此旋转前的位置需要记录一下,即parent、parL、parLR位置如上面的模型图所示:
parL就是parent的左孩子,parLR就是parL的右孩子
判断依据:
第一种情况,parRL位置就是插入的结点,所以平衡因子是0
第二种情况,插入在b1下,所以parRL平衡因子是-1
第三种情况,插入在b2下,所以parRL平衡因子是1
同样不管怎么旋转,只有parent、parL、parLR这三个位置的平衡因子变了,所以代码只需要改这三个位置的平衡因子
三、AVL树模拟实现
代码如下,具体都有注释:
一些头文件需要自己包,这里只给出实现的代码
template
struct AVLTreeNode
{
AVLTreeNode* _left;
AVLTreeNode* _right;
AVLTreeNode* _parent;
pair _kv;
int _bf;//平衡因子balance factor
//构造函数
AVLTreeNode(const pair& kv)
:_left(nullptr)
,_right(nullptr)
,_parent(nullptr)
,_kv(kv)
,_bf(0)
{}
};
template
struct AVLTree
{
typedef AVLTreeNode Node;
public:
bool insert(const pair& kv)
{
//如果AVL树为空,则用kv来new一个新结点
if (_root == nullptr)
{
_root = new Node(kv);
return true;
}
//遍历,直到找到空结点
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
//插入的值大于该结点
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
//插入的值小于该结点
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
//插入的值相等于该结点
else
{
return false;
}
}
//判断插入结点在父结点的左还是右
cur = new Node(kv);
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
//链接插入结点的parent
cur->_parent = parent;
//控制平衡
//平衡因子的更新按照博客的更新规则顺序
//最坏情况更新到parent,这时根结点的parent为空
while (parent)
{
//按照博客的更新规则顺序12345
//1、parent的平衡因子++或--
if (cur == parent->_left)
{
parent->_bf--;
}
else
{
parent->_bf++;
}
//2、parent的平衡因子绝对值为1
if (abs(parent->_bf) == 1)
{
parent = parent->_parent;
cur = cur->_parent;
}
//3、parent的平衡因子绝对值为0
else if (abs(parent->_bf) == 0)
{
break;
}
//4、parent的平衡因子绝对值为2
else if (abs(parent->_bf) == 2)
{
//parent所在的子树需要做旋转处理
//右右:左单旋
if (parent->_bf == 2 && cur->_bf == 1)
{
//左单旋
RotateL(parent);
}
else if (parent->_bf == -2 && cur->_bf == -1)
{
//右单旋
RotateR(parent);
}
else if (parent->_bf == -2 && cur->_bf == 1)
{
//左右双旋
RotateLR(parent);
}
else if (parent->_bf == 2 && cur->_bf == -1)
{
//右左双旋
RotateRL(parent);
}
//如果运行到下面的else,说明上面处理的有问题
//所以直接assert断言,结束程序
else
{
assert(false);
}
//旋转完成后退出
break;
}
//5、parent的平衡因子绝对值大于2
else
{
//abs(parnet->_bf) > 2
//程序运行到这,说明插入前就不是AVL树
assert(false);
}
}
return true;
}
bool IsAVLtree()
{
return _IsAVLtree(_root);
}
private:
//判断是否是AVL树
bool _IsAVLtree(Node* root)
{
//空树是AVL树
if (root == nullptr)
return true;
//判断左右字树的高度差是否满足AVL树
int leftHT = Height(root->_left);
int rightHT = Height(root->_right);
int num = rightHT - leftHT;
//比较左右字树减出来的平衡因子和父结点的平衡因子
//可以判断出平衡因子是否改变
if (root->_bf != num)
{
cout << root->_kv.first << "平衡因子错误" << endl;
return false;
}
return abs(num) < 2
&& _IsAVLtree(root->_left)
&& _IsAVLtree(root->_right);
}
//求树得高度
int Height(Node* root)
{
if (root == nullptr)
return 0;
int leftHT = Height(root->_left);
int rightHT = Height(root->_right);
return max(leftHT, rightHT) + 1;
}
//左单旋
void RotateL(Node* parent)
{
//parR和parRL是博客中的对应位置
//parR是parent的右孩子
//parRL是parR的左孩子
Node* parR = parent->_right;
Node* parRL = parR->_left;
parent->_right = parRL;
//链接_parent的关系
//可能出现parR为空的情况
if (parRL)
parRL->_parent = parent;
parR->_left = parent;
//记录一下parent->_parent,为下面的第二种情况
//平衡因子为2的结点是子树的根结点做准备
Node* parP = parent->_parent;
//链接_parent的关系
parent->_parent = parR;
//两种情况,平衡因子是2的结点是否是整棵树的根结点
//1、平衡因子为2的结点是整棵树的根结点
if (_root == parent)
{
_root = parR;
parR->_parent = nullptr;
}
//2、平衡因子为2的结点是子树的根结点
else
{
if (parP->_left == parent)
{
parP->_left = parR;
}
else
{
parP->_right = parR;
}
parR->_parent = parP;
}
//改变parent和parR的平衡因子,旋转完都为0
parent->_bf = parR->_bf = 0;
}
//右单旋
void RotateR(Node* parent)
{
//定义parL和parLR
//parL指parent的左子树
//parLR指parL的右子树
Node* parL = parent->_left;
Node* parLR = parL->_right;
parL->_right = parent;
//记录parent的_parent,为下面的情况2做准备
Node* parP = parent->_parent;
parent->_parent = parL;
parent->_left = parLR;
if (parLR)
parLR->_parent = parent;
//两种情况,平衡因子是-2的结点是否是整棵树的根结点
//1、平衡因子为-2的结点是整棵树的根结点
if (_root == parent)
{
_root = parL;
parL->_parent = nullptr;
}
//2、平衡因子为-2的结点是子树的根结点
else
{
if (parP->_left == parent)
{
parP->_left = parL;
}
else if (parP->_right == parent)
{
parP->_right = parL;
}
parL->_parent = parP;
}
parL->_bf = parent->_bf = 0;
}
//左右双旋
void RotateLR(Node* parent)
{
//记录parL和parLR
Node* parL = parent->_left;
Node* parLR = parL->_right;
//旋转前记录parLR的平衡因子,为了区分三种情况
int bf = parLR->_bf;
//先左单旋再右单旋,复用
RotateL(parent->_left);
RotateR(parent);
//三种不同情况的平衡因子更新分情况讨论
//三种情况的parLR平衡因子都是0
parLR->_bf = 0;
//1、旋转前parLR的平衡因子是0
if (bf == 0)
{
parent->_bf = 0;
parL = 0;
}
//2、旋转前parLR的平衡因子是1
else if (bf == 1)
{
parent->_bf = 0;
parL->_bf = -1;
}
//3、旋转前parLR的平衡因子是-1
else if (bf == -1)
{
parent->_bf = 1;
parL->_bf = 0;
}
//如果运行到下面的else,说明上面处理的有问题
//所以直接assert断言,结束程序
else
{
assert(false);
}
}
//右左双旋
void RotateRL(Node* parent)
{
//记录parR和parRL
Node* parR = parent->_right;
Node* parRL = parR->_left;
//旋转前记录parRL的平衡因子,为了区分三种情况
int bf = parRL->_bf;
//先右单旋再左单旋,复用
RotateR(parent->_right);
RotateL(parent);
//三种不同情况的平衡因子更新分情况讨论
//三种情况的parRL平衡因子都是0
parRL->_bf = 0;
//1、旋转前parRL 的平衡因子是0
if (bf == 0)
{
parent->_bf = 0;
parR = 0;
}
//2、旋转前parRL的平衡因子是1
else if (bf == 1)
{
parent->_bf = -1;
parR->_bf = 0;
}
//3、旋转前parRL的平衡因子是-1
else if (bf == -1)
{
parent->_bf = 0;
parR->_bf = 1;
}
//如果运行到下面的else,说明上面处理的有问题
//所以直接assert断言,结束程序
else
{
assert(false);
}
}
private:
Node* _root = nullptr;
};