【机器学习】详解回归(Regression)
文章目录
- 是什么的问题
- 案例说明
是什么的问题
- 回归分析(Regression Analysis) 是研究自变量与因变量之间数量变化关系的一种分析方法,它主要是通过因变量Y与影响它的自变量 X i ( i 1 , 2 , 3 … ) X_i(i1,2,3…) Xi(i1,2,3…)之间的回归模型,衡量自变量 X i X_i Xi对因变量Y的影响能力的,进而可以用来预测因变量Y的发展趋势。
- 损失函数(Cost Function/Lost Function) 用于估计模型的预测值和真实值之间的不一致程度,损失函数越小代表模型预测结果与真实值越相近。
定义线性回归的损失函数,可采用最小二乘法,通过最小化误差的平方和寻找数据的最佳函数匹配。
单个样本(example)的误差函数:
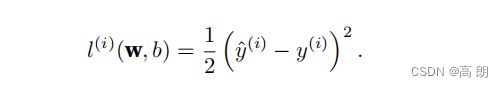
总体n的误差函数:
 线性回归模型的函数: y ^ = w 1 x 1 + w 2 x 2 + . . . + w d x d + b = W T X + b \hat{y}=w_1x_1+w_2x_2+...+w_dx_d+b=W^TX+b y^=w1x1+w2x2+...+wdxd+b=WTX+b
线性回归模型的函数: y ^ = w 1 x 1 + w 2 x 2 + . . . + w d x d + b = W T X + b \hat{y}=w_1x_1+w_2x_2+...+w_dx_d+b=W^TX+b y^=w1x1+w2x2+...+wdxd+b=WTX+b
在训练模型时,我们希望寻找⼀组参数(w∗, b∗),这组参数能最⼩化在所有训练样本上的总损失。

- 如何找到最优的w,b来优化我们的模型?
用数学的方法就是把w,b看成未知变量,分别对其求偏导。
L ( w , b ) = ∑ i = 1 n ( W T X + b i − y i ) 2 L(w,b)=\sum_{i=1}^{n} (W^TX+bi-y_i)^2 L(w,b)=i=1∑n(WTX+bi−yi)2
因为我们求L最小时,w和b的值,去掉前面的非0正系数不影响。
求参数w:
 求参数b:同上
求参数b:同上

案例说明
问题:预测宝可梦升级后的cp值
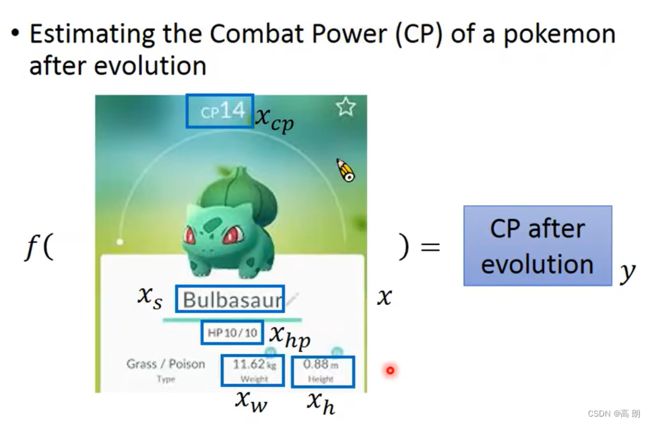 Step1: model (设计网络模型)define a set of function
Step1: model (设计网络模型)define a set of function
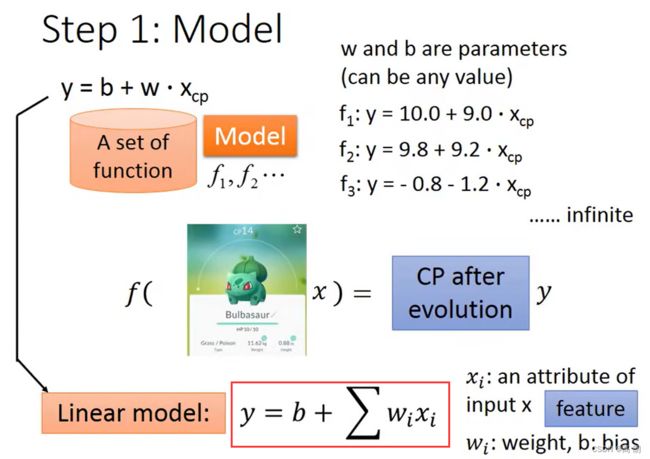
b是bias(偏置), w i w_i wi是weight(权重), X c p X_{cp} Xcp是我们输入的cp值
线性模型: y = b + w 1 x 1 + w 2 x 2 + . . . + w i x i y = b + w_1x_1 + w_2x_2 + ... + w_ix_i y=b+w1x1+w2x2+...+wixi
b和w的值是有很多个的,所以有a set of function,需要通过这个train data去找到这个最合适的function。
step 2: Goodness of function(函数的好坏)
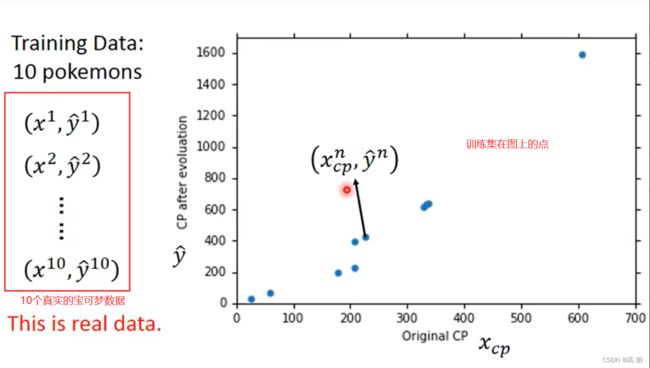 通过第一另外一个function:Loss来判断上面的function的好坏
通过第一另外一个function:Loss来判断上面的function的好坏
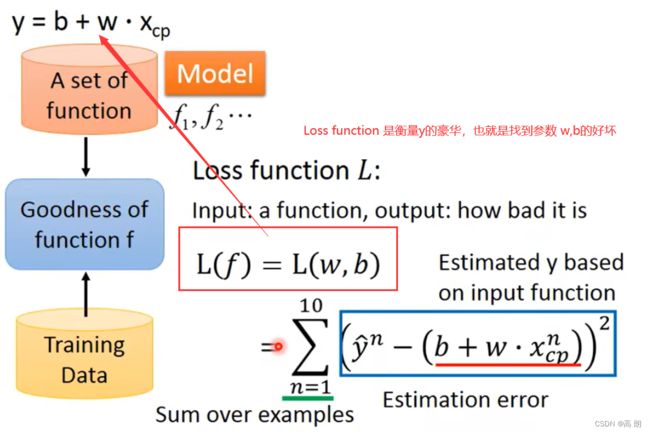 Loss function 是去衡量y的好坏,去判断我们找到的w,b的好坏
Loss function 是去衡量y的好坏,去判断我们找到的w,b的好坏
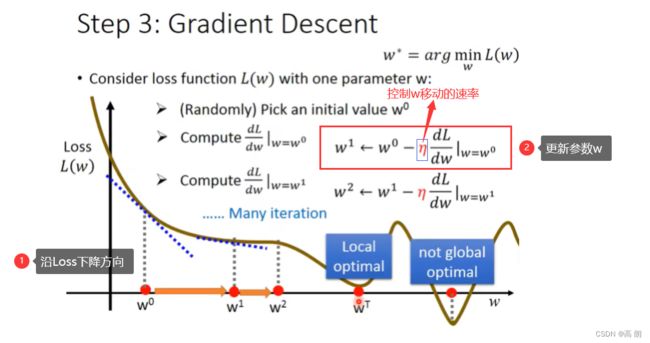
step 3: Best Funciton(Gradient Descent)
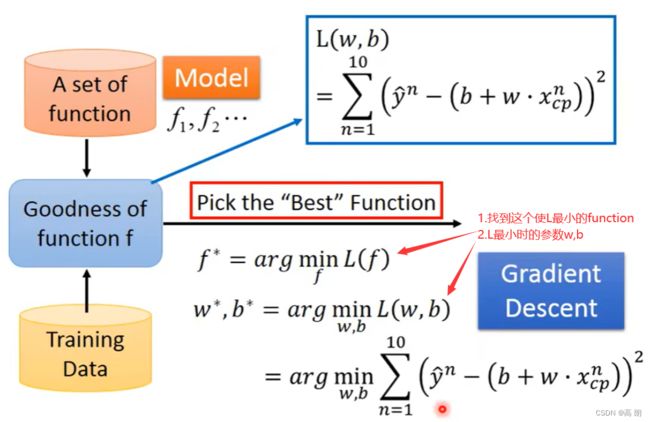 很显然,就是求L分别对w,b的偏导,通过梯度下降的方式来找到最小的L。
很显然,就是求L分别对w,b的偏导,通过梯度下降的方式来找到最小的L。
单个参数的考虑:
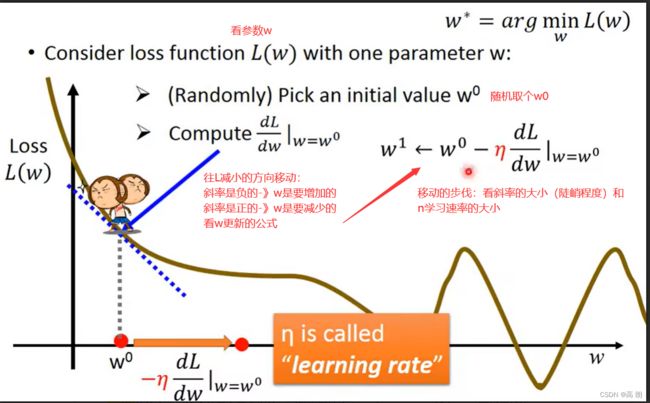 通过不断更新,使得L最小,会到达一个局部最优(local optimal),斜率为0或接近于0,这个时候就无法再更新w了,所以是不能找到全局最优(global optimal)。
通过不断更新,使得L最小,会到达一个局部最优(local optimal),斜率为0或接近于0,这个时候就无法再更新w了,所以是不能找到全局最优(global optimal)。
俩个参数的考虑:

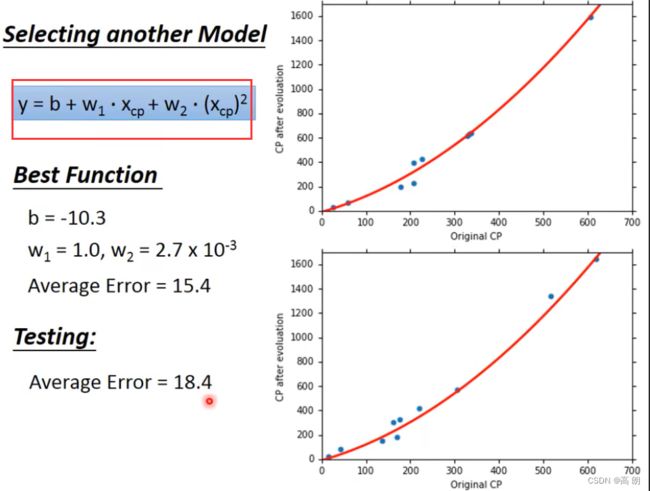
 最后,通过上面的10个宝可梦的数据,得到参数b,w,然后进行测试:
最后,通过上面的10个宝可梦的数据,得到参数b,w,然后进行测试:
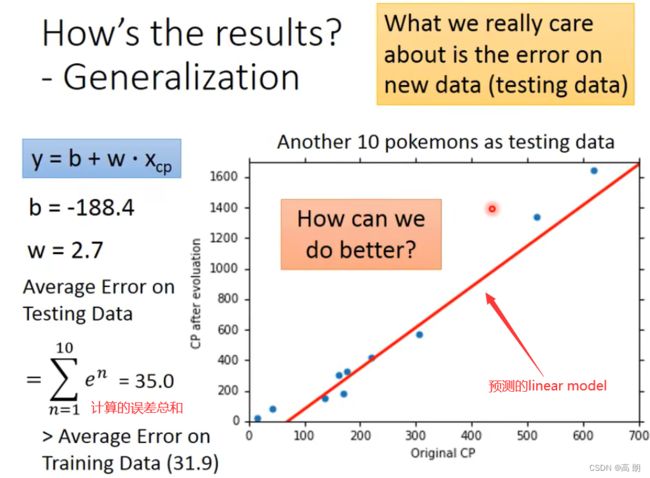
怎样获得更好的结果呢?怎样让预测更加准确呢?
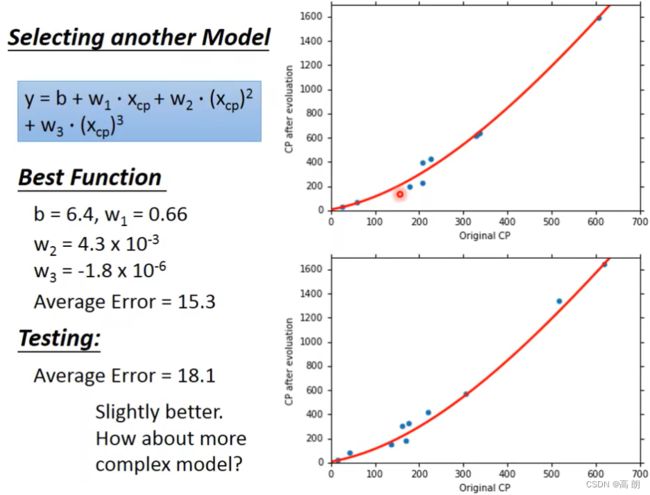
其实就是需要改变模型:(这里改成二次式)
多项式回归(Polynomial Regression), 多项式回归与线性回归的概念相同,只是它使用的是曲线而不是直线(线性回归使用的是直线)。多项式回归学习更多的参数来绘制非线性回归曲线。对于不能用直线概括的数据,它是有益的。多项式回归是将自变量x与因变量y之间的关系建模为n次多项式的一种线性回归形式。多项式回归拟合了x值与y相应条件均值之间的非线性关系,记为E(y |x)。
 四次:
四次:
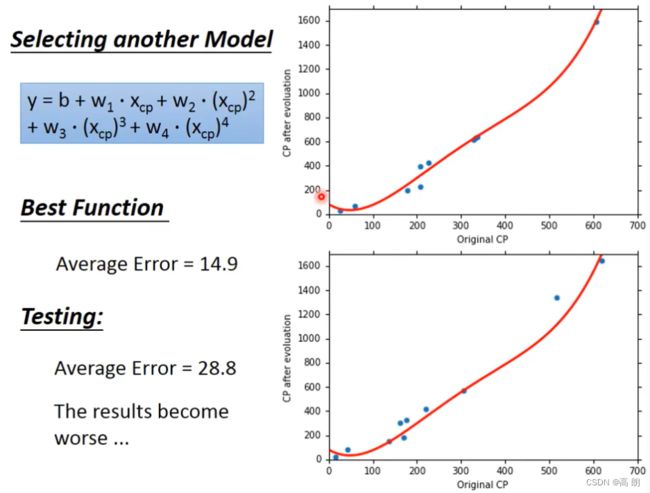 从这里开始,虽然换成了更复杂的Mode。但是测试的结果,average error变大了,results become worse…
从这里开始,虽然换成了更复杂的Mode。但是测试的结果,average error变大了,results become worse…
五次:
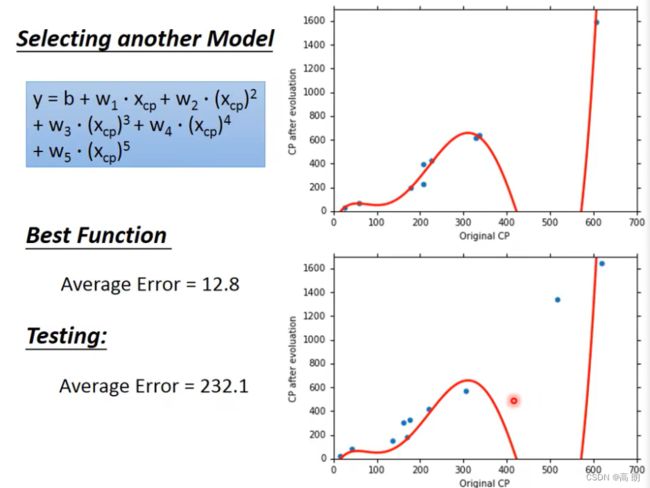 综上:
综上:
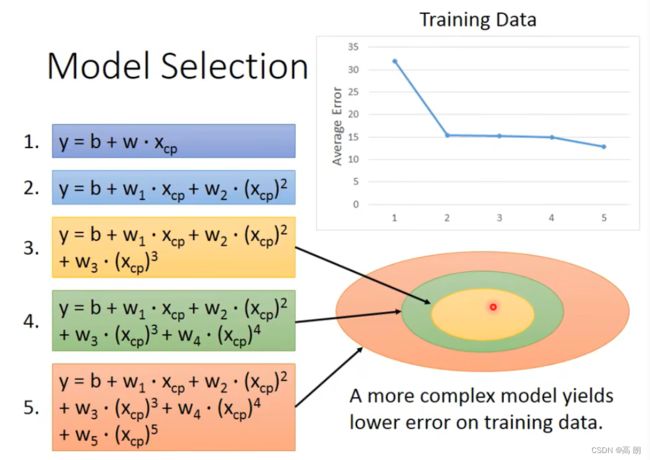 模型model越复杂,包含的train data越多,在训练集上的误差越小。
模型model越复杂,包含的train data越多,在训练集上的误差越小。
 但是更加复杂的模型不一定能在测试数据中带来更好的表现。会出现【过拟合】,所以,我们要选择一个最适合我们的model而不是最复杂的model。因为,可能会导致过拟合。上图中最好的model是三次式的。
但是更加复杂的模型不一定能在测试数据中带来更好的表现。会出现【过拟合】,所以,我们要选择一个最适合我们的model而不是最复杂的model。因为,可能会导致过拟合。上图中最好的model是三次式的。
当增加更多的宝可梦数据时,会发现不仅仅只有一个cp值的影响,还有物种的影响,所以需要重新设计我们的model

重新设计的model,增加了物种因素:
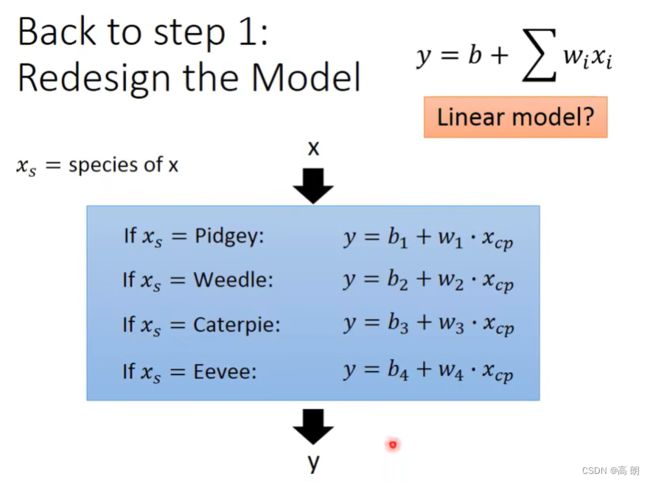 结果:
结果:
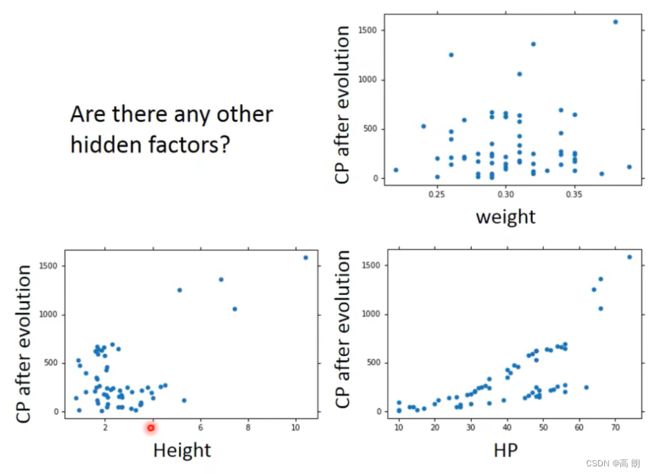
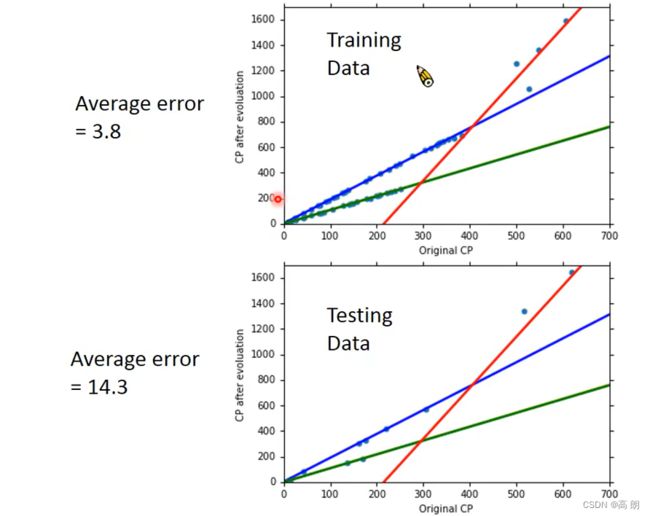 上分类后得到的linear model,结果明显比原来的没有分类的好太多了。尝试增加更多因素,修改model:(量,高度,HP值)
上分类后得到的linear model,结果明显比原来的没有分类的好太多了。尝试增加更多因素,修改model:(量,高度,HP值)
 重新设计的model:
重新设计的model:
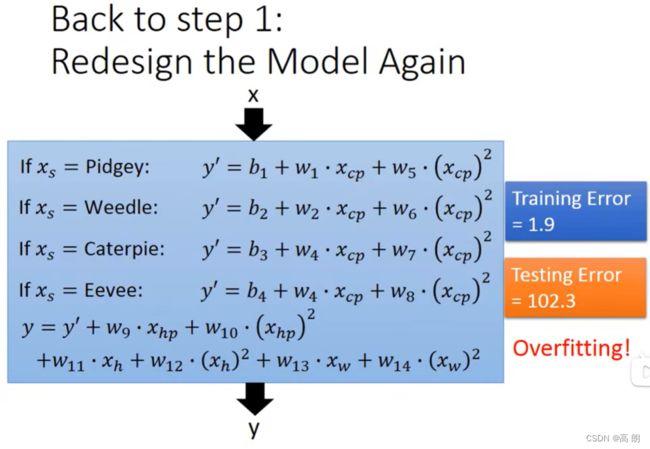 最终结果训练误差小了很多,但是测试误差太大了,过拟合了。遇到这个情况需要引出一个新的概念:正则化(Regularization)
最终结果训练误差小了很多,但是测试误差太大了,过拟合了。遇到这个情况需要引出一个新的概念:正则化(Regularization)
Back to step 2: Regularization(正则化) 正则化就是说给需要训练的目标函数加上一些规则(限制),让我们的函数尽量平缓,别过于膨胀,我们在梯度函数中加上 w e i g h t 2 weight^2 weight2这一项,这样就可以很好控制weight的大小。
 重新训练的结果:
重新训练的结果:
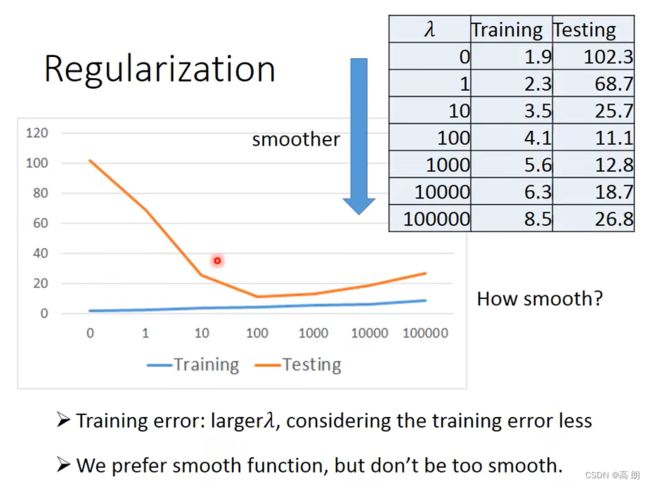 当λ=100时,达到这个模型的最佳测试Loss
当λ=100时,达到这个模型的最佳测试Loss