The Annotated Diffusion Model（翻译）

The Annotated Diffusion Model（翻译）

来源： https://huggingface.co/blog/annotated-diffusion
code:

在这篇博文中，我们将更深入地研究去噪扩散概率模型（也称为 DDPM、扩散模型、基于分数的生成模型或简称为自动编码器），因为研究人员已经能够使用它们在 (非)条件图像/音频/视频生成。流行的例子（在撰写本文时）包括OpenAI 的GLIDE和DALL-E 2 、海德堡大学的Latent Diffusion和Google Brain 的ImageGen 。

我们将回顾 ( Ho et al., 2020 ) 的原始 DDPM 论文，基于 Phil Wang 的实现在 PyTorch 中逐步实现它——它本身基于原始的 TensorFlow 实现。请注意，生成建模的扩散思想实际上已经在 ( Sohl-Dickstein et al., 2015 ) 中引入。然而，直到 ( Song et al., 2019 )（在斯坦福大学），然后 ( Ho et al., 2020 )（在谷歌大脑）才独立改进了该方法。

请注意，扩散模型有多种观点。在这里，我们采用离散时间（潜在变量模型）视角，但一定要检查其他视角。

我们将首先安装并导入所需的库

!pip install -q -U einops datasets matplotlib tqdm

import math
from inspect import isfunction
from functools import partial

%matplotlib inline
import matplotlib.pyplot as plt
from tqdm.auto import tqdm
from einops import rearrange, reduce
from einops.layers.torch import Rearrange

import torch
from torch import nn, einsum
import torch.nn.functional as F

什么是扩散模型

关于图像的更多细节，设置包括 2 个过程：

• 一个固定的（或预定义的）前向扩散过程$q$我们选择的，逐渐将高斯噪声添加到图像中，直到最终得到纯噪声
• 学习反向去噪扩散过程$p_{\theta }$的，其中训练神经网络从纯噪声开始逐渐对图像进行去噪，直到最终得到实际图像。
  
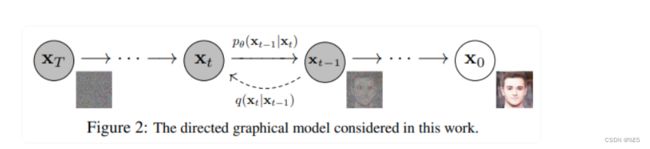
  由 t 索引的正向和反向过程都发生在一定数量的有限时间步长 T（DDPM 作者使用 T=1000）。 您从 t=0 开始，从数据分布中采样真实图像 xo（假设是来自 ImageNet 的猫图像），并且正向过程在每个时间步 t 从高斯分布中采样一些噪声，这些噪声被添加到 上一个时间步的图像。 给定足够大的 T 和在每个时间步添加噪声的良好表现时间表，您最终会通过渐进过程在 t=T 处得到所谓的各向同性高斯分布。

以更数学的形式

让我们更正式地写下来，因为最终我们需要一个可处理的损失函数，我们的神经网络需要优化它。
设$q\left({\mathbf{x}}_0\right)$为真实的数据分布，比如“真实图像”。我们可以从这个分布中抽样得到图像${\mathbf{x}}_0\sim q\left({\mathbf{x}}_0\right)$。我们定义了前向扩散过程$q\left({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1}\right)$，根据已知的方差调度$0<{\beta }_1<{\beta }_2<\dots <{\beta }_T<1$在每个时间步$t$上加入高斯噪声
$$q\left({\mathbf{x}}_t\mid {\mathbf{x}}_{t-1}\right)=\mathcal{N}\left({\mathbf{x}}_t;\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1},{\beta }_t\mathbf{I}\right)$$

回想一下，正态分布(也称为高斯分布)由两个参数定义:平均值$\mu$和方差${\sigma }^2\ge 0$。基本上，在时间步长t上的每个新的(稍微有噪声的)图像都是从具有${\mu }_t=\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1}$和${\sigma }_t^2={\beta }_t$的条件高斯分布中绘制的，我们可以通过对$ϵ\sim \mathcal{N}(0,\mathbf{I})$采样然后设置${\mathbf{x}}_t=\sqrt{1-{\beta }_t}{\mathbf{x}}_{t-1}+\sqrt{{\beta }_t}ϵ$来实现。

请注意，${\beta }_t$在每个时间步t上不是恒定的(因此下标)——事实上，我们定义了一个所谓的“方差计划”，它可以是线性的，二次的，余弦的，等等，我们将进一步看到。

所以从$x_0$开始，我们最终得到${\mathbf{x}}_1,\dots ,{\mathbf{x}}_t,\dots ,{\mathbf{x}}_T$，其中$x_T$是纯高斯噪声如果我们适当地设置调度。

现在，如果我们知道条件分布$p(x_{t-1}|x_t)$，那么我们可以将过程倒转：通过采样一些随机的高斯噪声$x_T$，然后逐渐“去噪”，以便最终得到来自真实分布$x_0$的样本。

然而，我们不知道 $p(x_{t-1}|x_t)$。它很难处理，因为它需要知道所有可能图像的分布，以便计算这个条件概率。因此，我们将利用神经网络来近似（学习）这个条件概率分布，我们称之为$p_{\theta }(x_{t-1}\mid x_t)$，其中$\theta$是神经网络的参数，通过梯度下降进行更新。

我们需要一个神经网络来表示逆向过程的(条件)概率分布。如果我们假设这个反向过程也是高斯分布，那么回想一下，任何高斯分布都是由两个参数定义的

• 均值参数化为${\mu }_{\theta }$
• 方差参数化为${\Sigma }_{\theta }$

我们可以把这个过程参数化为
$p_{\theta }\left({\mathbf{x}}_{t-1}\mid {\mathbf{x}}_t\right)=\mathcal{N}\left({\mathbf{x}}_{t-1};{\mu }_{\theta }\left({\mathbf{x}}_t,t\right),{\Sigma }_{\theta }\left({\mathbf{x}}_t,t\right)\right)$

其中均值和方差也取决于噪声水平t。
因此，我们的神经网络需要学习/表征均值和差异。但是，DDPM作者决定将方差固定，并让神经网络仅学习（表示该条件概率分布的平均${\mu }_{\theta }$）。从Paper：

“First, we set ${\Sigma }_{\theta }\left({\mathbf{x}}_t,t\right)={\sigma }_t^2\mathbf{I}$ to untrained time dependent constants. Experimentally, both ${\sigma }_t^2={\beta }_t$ and ${\sigma }_t^2={\tilde{\beta }}_t$ (see paper) had similar results.”

这在后来的 Improved diffusion models论文中得到了改进，其中神经网络除了学习均值之外，还学习了这个反向过程的方差。

因此，我们继续前进，假设我们的神经网络只需要学习/表征此条件概率分布的平均值。

定义目标函数(通过重新参数化平均值)

为了推导出一个目标函数来学习后向过程的均值，作者观察到$q$和$p_{\theta }$的组合可以被看作是一个变分自编码器(VAE) (Kingma et al.，2013)。因此，变分下界(也称为ELBO)可用于最小化相对于真实数据样本$x_0$的负对数似然(我们参考VAE论文了解有关ELBO的详细信息)。结果表明，这个过程的ELBO是每个时间步长t的损失之和$L=L_0+L_1+\dots +L_T$。通过前向$q$过程和后向过程的构造，损失的每一项($L_0$除外)实际上是两个高斯分布之间的KL散度，可以明确地写成相对于均值的l2损失。
正如Sohl-Dickstein等人所示，构建的前向过程$q$的直接结果是，我们可以在任何以$x_0$为条件的任意噪声水平下进行采样$x_t$(因为高斯函数的和也是高斯函数)。这是非常方便的:我们不需要重复应用$q$来采样$x_t$。我们有这个
$$q\left({\mathbf{x}}_t\mid {\mathbf{x}}_0\right)=\mathcal{N}\left({\mathbf{x}}_t;\sqrt{{\bar{\alpha }}_t}{\mathbf{x}}_0,\left(1-{\bar{\alpha }}_t\right)\mathbf{I}\right)$$

关于${\alpha }_t:=1-{\beta }_t$ 和 ${\bar{\alpha }}_t:={\Pi }_{s=1}^t{\alpha }_s$。我们把这个方程称为“漂亮的性质”。这意味着我们可以对高斯噪声进行采样并适当缩放，并将其添加到$x_0$直接得到$x_t$。注意，${\bar{\alpha }}_t$是已知${\beta }_t$方差表的函数，因此也是已知的，并且可以预先计算。这允许我们在训练期间优化损失函数$L$的随机项(或者换句话说，在训练期间随机采样$t$并优化$L_t$)。这个性质的另一个优点，正如Ho等人所示，是可以通过重新参数化均值来使神经网络学习（预测）添加的噪声（通过网络${ϵ}_{\theta }\left({\mathbf{x}}_t,t\right)$）以达到噪声级别$t$在构成损失的KL项中。具体的数学推导请参考这篇优秀的博客文章。这意味着我们的神经网络变成了一个噪声预测器，而不是(直接)均值预测器。平均值的计算方法如下:
$${\mu }_{\theta }\left({\mathbf{x}}_t,t\right)=\frac{1}{\sqrt{{\alpha }_t}}\left({\mathbf{x}}_t-\frac{{\beta }_t}{\sqrt{1-{\bar{\alpha }}_t}}{ϵ}_{\theta }\left({\mathbf{x}}_t,t\right)\right)$$

最终目标函数$L_t$看起来如下(对于给定$ϵ\sim \mathcal{N}(0,\mathbf{I})$的随机时间步长$t$)
∥ ϵ − ϵ θ ( x t , t ) ∥ 2 = ∥ ϵ − ϵ θ ( α ˉ t x 0 + ( 1 − α ˉ t ) ϵ , t ) ∥ 2 \left\|\epsilon-\epsilon_\theta\left(\mathbf{x}_t, t\right)\right\|^2=\left\|\epsilon-\epsilon_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{\left(1-\bar{\alpha}_t\right)} \epsilon, t\right)\right\|^2 ∥ϵ−ϵθ​(xt​,t)∥2= ​ϵ−ϵθ​(αˉt​ ​x0​+(1−αˉt​) ​ϵ,t) ​2
这里，$x_0$是初始的(真实的，未损坏的)图像，我们看到固定前向过程给出的直接噪声水平 t 样本。λ是在时间步长t采样的纯噪声，λ是我们的神经网络。$ϵ$ 是在时间步骤 $t$ 上采样的纯噪声，而 ${ϵ}_{\theta }(x_t,t)$ 是我们的神经网络。
训练算法现在看起来如下:

换言之:

• 我们从真实的未知和可能复杂的数据分布$q(x_0)$中取一个随机样本$x_0$
• 我们在1和t之间均匀采样噪声电平t(即，随机时间步长)。
• 我们从高斯分布中采样一些噪声，并在 t 级通过这种噪声破坏输入（使用上面定义的 nice 属性）
• 神经网络被训练为基于损坏的图像 $x_t$ 预测此噪声（即基于已知调度器${\beta }_t)$ 应用于 $X_0$ 的噪声）

实际上，所有这些都是在批量数据上完成的，因为人们使用随机梯度下降来优化神经网络。

神经网络

他的神经网络需要在特定的时间步骤中拍摄噪声图像并返回预测的噪声。请注意，预测的噪声是张量，其大小/分辨率与输入图像相同。因此，从技术上讲，网络吸收并输出相同形状的张量。我们可以使用哪种类型的神经网络？

这里使用的通常与Autoencoder非常相似，您可能还记得典型的“深度学习入门”教程。自动编码器在编码器和解码器之间有一个所谓的“瓶颈”层。编码器首先将图像编码成一个较小的隐藏表示，称为“瓶颈”，然后解码器将该隐藏表示解码回实际图像。这迫使网络只在瓶颈层保留最重要的信息。

在架构方面，DDPM的作者选择了由 (Ronneberger et al., 2015)引入的U-Net(当时在医学图像分割方面取得了最先进的结果)。这个网络，像任何自动编码器一样，由中间的瓶颈组成，以确保网络只学习最重要的信息。重要的是，它引入了编码器和解码器之间的残差连接，极大地改善了梯度流(inspired by ResNet in He et al., 2015)。

可以看出，U-Net模型首先对输入进行下采样(即使输入在空间分辨率方面更小)，然后进行上采样。

下面，我们一步一步地实现这个网络。

网络助手

首先，我们定义了一些在实现神经网络时会用到的辅助函数和类。重要的是，我们定义了一个残差模块，它简单地将输入添加到特定函数的输出(换句话说，将残差连接添加到特定函数)。

我们还定义了上下采样操作的别名。

def exists(x):
    return x is not None

def default(val, d):
    if exists(val):
        return val
    return d() if isfunction(d) else d


def num_to_groups(num, divisor):
    groups = num // divisor
    remainder = num % divisor
    arr = [divisor] * groups
    if remainder > 0:
        arr.append(remainder)
    return arr


class Residual(nn.Module):
    def __init__(self, fn):
        super().__init__()
        self.fn = fn

    def forward(self, x, *args, **kwargs):
        return self.fn(x, *args, **kwargs) + x


def Upsample(dim, dim_out=None):
    return nn.Sequential(
        nn.Upsample(scale_factor=2, mode="nearest"),
        nn.Conv2d(dim, default(dim_out, dim), 3, padding=1),
    )


def Downsample(dim, dim_out=None):
    # No More Strided Convolutions or Pooling
    return nn.Sequential(
        Rearrange("b c (h p1) (w p2) -> b (c p1 p2) h w", p1=2, p2=2),
        nn.Conv2d(dim * 4, default(dim_out, dim), 1),
    )

位置嵌入

由于神经网络的参数是随时间(噪声水平)共享的，受Transformer (Vaswani et al.， 2017)的启发，作者采用正弦位置嵌入对其进行编码。对于批处理中的每个图像, 使得神经网络“know”它在哪个特定的时间步长(噪声水平)运行的。

SinusoidalPositionEmbeddings 模块将形状为 (batch_size, 1) 的张量作为输入（即一批中几个噪声图像的噪声水平），并将其转换为形状为 (batch_size, dim) 的张量，其中 dim 是图像的维数 位置嵌入。 然后将其添加到每个残差块中，我们将进一步看到。

class SinusoidalPositionEmbeddings(nn.Module):
    def __init__(self, dim):
        super().__init__()
        self.dim = dim

    def forward(self, time):
        device = time.device
        half_dim = self.dim // 2
        embeddings = math.log(10000) / (half_dim - 1)
        embeddings = torch.exp(torch.arange(half_dim, device=device) * -embeddings)
        embeddings = time[:, None] * embeddings[None, :]
        embeddings = torch.cat((embeddings.sin(), embeddings.cos()), dim=-1)
        return embeddings

ResNet block

接下来，我们定义 U-Net 模型的核心构建块。 DDPM 作者采用了 Wide ResNet Block(Zagoruyko et al., 2016)，但 Phil Wang 已将标准卷积层替换为“权重标准化”版本，该版本与组归一化结合使用效果更好（参见(Kolesnikov et al., 2019)了解详情）。

class WeightStandardizedConv2d(nn.Conv2d):
    """
    https://arxiv.org/abs/1903.10520
    weight standardization purportedly works synergistically with group normalization
    """

    def forward(self, x):
        eps = 1e-5 if x.dtype == torch.float32 else 1e-3

        weight = self.weight
        mean = reduce(weight, "o ... -> o 1 1 1", "mean")
        var = reduce(weight, "o ... -> o 1 1 1", partial(torch.var, unbiased=False))
        normalized_weight = (weight - mean) * (var + eps).rsqrt()

        return F.conv2d(
            x,
            normalized_weight,
            self.bias,
            self.stride,
            self.padding,
            self.dilation,
            self.groups,
        )


class Block(nn.Module):
    def __init__(self, dim, dim_out, groups=8):
        super().__init__()
        self.proj = WeightStandardizedConv2d(dim, dim_out, 3, padding=1)
        self.norm = nn.GroupNorm(groups, dim_out)
        self.act = nn.SiLU()

    def forward(self, x, scale_shift=None):
        x = self.proj(x)
        x = self.norm(x)

        if exists(scale_shift):
            scale, shift = scale_shift
            x = x * (scale + 1) + shift

        x = self.act(x)
        return x


class ResnetBlock(nn.Module):
    """https://arxiv.org/abs/1512.03385"""

    def __init__(self, dim, dim_out, *, time_emb_dim=None, groups=8):
        super().__init__()
        self.mlp = (
            nn.Sequential(nn.SiLU(), nn.Linear(time_emb_dim, dim_out * 2))
            if exists(time_emb_dim)
            else None
        )

        self.block1 = Block(dim, dim_out, groups=groups)
        self.block2 = Block(dim_out, dim_out, groups=groups)
        self.res_conv = nn.Conv2d(dim, dim_out, 1) if dim != dim_out else nn.Identity()

    def forward(self, x, time_emb=None):
        scale_shift = None
        if exists(self.mlp) and exists(time_emb):
            time_emb = self.mlp(time_emb)
            time_emb = rearrange(time_emb, "b c -> b c 1 1")
            scale_shift = time_emb.chunk(2, dim=1)

        h = self.block1(x, scale_shift=scale_shift)
        h = self.block2(h)
        return h + self.res_conv(x)

注意力模块

接下来，我们定义了注意力模块，DDPM的作者将其添加到卷积块之间。注意力是著名的Transformer架构的基石(Vaswani et al.， 2017)，该架构在人工智能的各个领域取得了巨大成功，从自然语言处理和视觉到蛋白质折叠。Phil Wang采用了两种注意力变体:一种是常规多头自我注意(如Transformer中使用的)，另一种是线性注意变体(Shen et al., 2018)，其时间和记忆需求在序列长度上呈线性，而不是常规注意的二次方。

关于注意力机制的详细解释，我们建议读者阅读Jay Allamar的一篇精彩的博客文章。

class Attention(nn.Module):
    def __init__(self, dim, heads=4, dim_head=32):
        super().__init__()
        self.scale = dim_head**-0.5
        self.heads = heads
        hidden_dim = dim_head * heads
        self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, bias=False)
        self.to_out = nn.Conv2d(hidden_dim, dim, 1)

    def forward(self, x):
        b, c, h, w = x.shape
        qkv = self.to_qkv(x).chunk(3, dim=1)
        q, k, v = map(
            lambda t: rearrange(t, "b (h c) x y -> b h c (x y)", h=self.heads), qkv
        )
        q = q * self.scale

        sim = einsum("b h d i, b h d j -> b h i j", q, k)
        sim = sim - sim.amax(dim=-1, keepdim=True).detach()
        attn = sim.softmax(dim=-1)

        out = einsum("b h i j, b h d j -> b h i d", attn, v)
        out = rearrange(out, "b h (x y) d -> b (h d) x y", x=h, y=w)
        return self.to_out(out)

class LinearAttention(nn.Module):
    def __init__(self, dim, heads=4, dim_head=32):
        super().__init__()
        self.scale = dim_head**-0.5
        self.heads = heads
        hidden_dim = dim_head * heads
        self.to_qkv = nn.Conv2d(dim, hidden_dim * 3, 1, bias=False)

        self.to_out = nn.Sequential(nn.Conv2d(hidden_dim, dim, 1), 
                                    nn.GroupNorm(1, dim))

    def forward(self, x):
        b, c, h, w = x.shape
        qkv = self.to_qkv(x).chunk(3, dim=1)
        q, k, v = map(
            lambda t: rearrange(t, "b (h c) x y -> b h c (x y)", h=self.heads), qkv
        )

        q = q.softmax(dim=-2)
        k = k.softmax(dim=-1)

        q = q * self.scale
        context = torch.einsum("b h d n, b h e n -> b h d e", k, v)

        out = torch.einsum("b h d e, b h d n -> b h e n", context, q)
        out = rearrange(out, "b h c (x y) -> b (h c) x y", h=self.heads, x=h, y=w)
        return self.to_out(out)

Group normalization

DDPM作者将U-NET的卷积/注意层与组归一化 (Wu et al., 2018)交织在一起。在下面，我们定义了一个序列类，该类别将用于在注意力层之前应用群态，正如我们将进一步看到的那样。请注意，关于在Transformers中是否在注意力之前还是之后是否施加归一化的争论。

class PreNorm(nn.Module):
    def __init__(self, dim, fn):
        super().__init__()
        self.fn = fn
        self.norm = nn.GroupNorm(1, dim)

    def forward(self, x):
        x = self.norm(x)
        return self.fn(x)

条件U-Net

现在，我们已经定义了所有的构建块（位置嵌入、ResNet 块、注意力和组归一化），是时候定义整个神经网络了。回想一下，网络${ϵ}_{\theta }\left({\mathbf{x}}_t,t\right)$的工作是接收一批噪声图像及其相应的噪声水平，并输出添加到输入中的噪声。更正式地说：

• 该网络将一批形状(batch size, num channels, height, width)的噪声图像和一批形状(batch size, num channels, height, width)的噪声水平作为输入，并返回一个形状张量(batch size, num channels, height, width)。

网络构建如下:

• 首先，在一批噪声图像上应用卷积层，并计算噪声水平的位置嵌入
• 接下来，应用一系列下采样阶段。每个下采样阶段由2个ResNet块+群规范+注意+残差连接+下采样操作组成
• 在网络的中间，再次应用ResNet块，与注意力交错
• 接下来，应用一系列上采样阶段。每个上采样阶段由2个ResNet块+群规范+注意+残基连接+上采样操作组成
• 最后，应用一个ResNet块和一个卷积层。

最终，神经网络堆积了层，好像它们是乐高积木（但要了解它们的工作方式很重要）。

class Unet(nn.Module):
    def __init__(
        self,
        dim,
        init_dim=None,
        out_dim=None,
        dim_mults=(1, 2, 4, 8),
        channels=3,
        self_condition=False,
        resnet_block_groups=4,
    ):
        super().__init__()

        # determine dimensions
        self.channels = channels
        self.self_condition = self_condition
        input_channels = channels * (2 if self_condition else 1)

        init_dim = default(init_dim, dim)
        self.init_conv = nn.Conv2d(input_channels, init_dim, 1, padding=0) # changed to 1 and 0 from 7,3

        dims = [init_dim, *map(lambda m: dim * m, dim_mults)]
        in_out = list(zip(dims[:-1], dims[1:]))

        block_klass = partial(ResnetBlock, groups=resnet_block_groups)

        # time embeddings
        time_dim = dim * 4

        self.time_mlp = nn.Sequential(
            SinusoidalPositionEmbeddings(dim),
            nn.Linear(dim, time_dim),
            nn.GELU(),
            nn.Linear(time_dim, time_dim),
        )

        # layers
        self.downs = nn.ModuleList([])
        self.ups = nn.ModuleList([])
        num_resolutions = len(in_out)

        for ind, (dim_in, dim_out) in enumerate(in_out):
            is_last = ind >= (num_resolutions - 1)

            self.downs.append(
                nn.ModuleList(
                    [
                        block_klass(dim_in, dim_in, time_emb_dim=time_dim),
                        block_klass(dim_in, dim_in, time_emb_dim=time_dim),
                        Residual(PreNorm(dim_in, LinearAttention(dim_in))),
                        Downsample(dim_in, dim_out)
                        if not is_last
                        else nn.Conv2d(dim_in, dim_out, 3, padding=1),
                    ]
                )
            )

        mid_dim = dims[-1]
        self.mid_block1 = block_klass(mid_dim, mid_dim, time_emb_dim=time_dim)
        self.mid_attn = Residual(PreNorm(mid_dim, Attention(mid_dim)))
        self.mid_block2 = block_klass(mid_dim, mid_dim, time_emb_dim=time_dim)

        for ind, (dim_in, dim_out) in enumerate(reversed(in_out)):
            is_last = ind == (len(in_out) - 1)

            self.ups.append(
                nn.ModuleList(
                    [
                        block_klass(dim_out + dim_in, dim_out, time_emb_dim=time_dim),
                        block_klass(dim_out + dim_in, dim_out, time_emb_dim=time_dim),
                        Residual(PreNorm(dim_out, LinearAttention(dim_out))),
                        Upsample(dim_out, dim_in)
                        if not is_last
                        else nn.Conv2d(dim_out, dim_in, 3, padding=1),
                    ]
                )
            )

        self.out_dim = default(out_dim, channels)

        self.final_res_block = block_klass(dim * 2, dim, time_emb_dim=time_dim)
        self.final_conv = nn.Conv2d(dim, self.out_dim, 1)

    def forward(self, x, time, x_self_cond=None):
        if self.self_condition:
            x_self_cond = default(x_self_cond, lambda: torch.zeros_like(x))
            x = torch.cat((x_self_cond, x), dim=1)

        x = self.init_conv(x)
        r = x.clone()

        t = self.time_mlp(time)

        h = []

        for block1, block2, attn, downsample in self.downs:
            x = block1(x, t)
            h.append(x)

            x = block2(x, t)
            x = attn(x)
            h.append(x)

            x = downsample(x)

        x = self.mid_block1(x, t)
        x = self.mid_attn(x)
        x = self.mid_block2(x, t)

        for block1, block2, attn, upsample in self.ups:
            x = torch.cat((x, h.pop()), dim=1)
            x = block1(x, t)

            x = torch.cat((x, h.pop()), dim=1)
            x = block2(x, t)
            x = attn(x)

            x = upsample(x)

        x = torch.cat((x, r), dim=1)

        x = self.final_res_block(x, t)
        return self.final_conv(x)

定义正向扩散过程

前向扩散过程在若干时间步长$T$中逐渐将噪声从实分布中添加到图像中，这是根据方差表进行的。最初的DDPM作者采用线性调度器。

我们将前向过程方差设为常数，从${\beta }_1=10^{-4}\text{ to }{\beta }_T=0.02$
然而，在 (Nichol et al., 2021)中表明，采用余弦时间表可以取得更好的结果。

下面，我们将为$T$个时间步骤定义各种调度(稍后我们将选择一个)。

def cosine_beta_schedule(timesteps, s=0.008):
    """
    cosine schedule as proposed in https://arxiv.org/abs/2102.09672
    """
    steps = timesteps + 1
    x = torch.linspace(0, timesteps, steps)
    alphas_cumprod = torch.cos(((x / timesteps) + s) / (1 + s) * torch.pi * 0.5) ** 2
    alphas_cumprod = alphas_cumprod / alphas_cumprod[0]
    betas = 1 - (alphas_cumprod[1:] / alphas_cumprod[:-1])
    return torch.clip(betas, 0.0001, 0.9999)

def linear_beta_schedule(timesteps):
    beta_start = 0.0001
    beta_end = 0.02
    return torch.linspace(beta_start, beta_end, timesteps)

def quadratic_beta_schedule(timesteps):
    beta_start = 0.0001
    beta_end = 0.02
    return torch.linspace(beta_start**0.5, beta_end**0.5, timesteps) ** 2

def sigmoid_beta_schedule(timesteps):
    beta_start = 0.0001
    beta_end = 0.02
    betas = torch.linspace(-6, 6, timesteps)
    return torch.sigmoid(betas) * (beta_end - beta_start) + beta_start

首先，让我们使用T=300个时间步长的线性调度，并从bt中定义我们需要的各种变量，例如方差T的累积积。下面的每个变量只是一维张量，存储从T到T的值。重要的是，我们还定义了一个提取函数，它将允许我们为一批指标提取适当的T指标。

timesteps = 300

# define beta schedule
betas = linear_beta_schedule(timesteps=timesteps)

# define alphas 
alphas = 1. - betas
alphas_cumprod = torch.cumprod(alphas, axis=0)
alphas_cumprod_prev = F.pad(alphas_cumprod[:-1], (1, 0), value=1.0)
sqrt_recip_alphas = torch.sqrt(1.0 / alphas)

# calculations for diffusion q(x_t | x_{t-1}) and others
sqrt_alphas_cumprod = torch.sqrt(alphas_cumprod)
sqrt_one_minus_alphas_cumprod = torch.sqrt(1. - alphas_cumprod)

# calculations for posterior q(x_{t-1} | x_t, x_0)
posterior_variance = betas * (1. - alphas_cumprod_prev) / (1. - alphas_cumprod)

def extract(a, t, x_shape):
    batch_size = t.shape[0]
    out = a.gather(-1, t.cpu())
    return out.reshape(batch_size, *((1,) * (len(x_shape) - 1))).to(t.device)

我们将用猫的图像来说明在扩散过程的每个时间步骤中是如何添加噪声的。

from PIL import Image
import requests

url = 'http://images.cocodataset.org/val2017/000000039769.jpg'
image = Image.open(requests.get(url, stream=True).raw)
image

噪声被添加到PyTorch张量中，而不是枕头图像。我们将首先定义图像转换，它允许我们从PIL图像转换为PyTorch张量(我们可以在其上添加噪声)，反之亦然。

这些转换相当简单:我们首先通过除以255对图像进行规范化(这样它们就在[0,1]范围内)，然后确保它们在[-1,1]范围内。从DPPM Paper

from torchvision.transforms import Compose, ToTensor, Lambda, ToPILImage, CenterCrop, Resize

image_size = 128
transform = Compose([
    Resize(image_size),
    CenterCrop(image_size),
    ToTensor(), # turn into Numpy array of shape HWC, divide by 255
    Lambda(lambda t: (t * 2) - 1),
    
])

x_start = transform(image).unsqueeze(0)
x_start.shape

我们还定义了反向变换，它接受一个PyTorch张量，其中包含[1,1][1,1]中的值，并将它们转换回PIL图像

import numpy as np

reverse_transform = Compose([
     Lambda(lambda t: (t + 1) / 2),
     Lambda(lambda t: t.permute(1, 2, 0)), # CHW to HWC
     Lambda(lambda t: t * 255.),
     Lambda(lambda t: t.numpy().astype(np.uint8)),
     ToPILImage(),
])

我们来验证一下

reverse_transform(x_start.squeeze())

现在我们可以像文中那样定义正向扩散过程

# forward diffusion (using the nice property)
def q_sample(x_start, t, noise=None):
    if noise is None:
        noise = torch.randn_like(x_start)

    sqrt_alphas_cumprod_t = extract(sqrt_alphas_cumprod, t, x_start.shape)
    sqrt_one_minus_alphas_cumprod_t = extract(
        sqrt_one_minus_alphas_cumprod, t, x_start.shape
    )

    return sqrt_alphas_cumprod_t * x_start + sqrt_one_minus_alphas_cumprod_t * noise

让我们在一个特定的时间步上进行测试

def get_noisy_image(x_start, t):
  # add noise
  x_noisy = q_sample(x_start, t=t)

  # turn back into PIL image
  noisy_image = reverse_transform(x_noisy.squeeze())

  return noisy_image

# take time step
t = torch.tensor([40])

get_noisy_image(x_start, t)

我们来看看不同的时间步长

import matplotlib.pyplot as plt

# use seed for reproducability
torch.manual_seed(0)

# source: https://pytorch.org/vision/stable/auto_examples/plot_transforms.html#sphx-glr-auto-examples-plot-transforms-py
def plot(imgs, with_orig=False, row_title=None, **imshow_kwargs):
    if not isinstance(imgs[0], list):
        # Make a 2d grid even if there's just 1 row
        imgs = [imgs]

    num_rows = len(imgs)
    num_cols = len(imgs[0]) + with_orig
    fig, axs = plt.subplots(figsize=(200,200), nrows=num_rows, ncols=num_cols, squeeze=False)
    for row_idx, row in enumerate(imgs):
        row = [image] + row if with_orig else row
        for col_idx, img in enumerate(row):
            ax = axs[row_idx, col_idx]
            ax.imshow(np.asarray(img), **imshow_kwargs)
            ax.set(xticklabels=[], yticklabels=[], xticks=[], yticks=[])

    if with_orig:
        axs[0, 0].set(title='Original image')
        axs[0, 0].title.set_size(8)
    if row_title is not None:
        for row_idx in range(num_rows):
            axs[row_idx, 0].set(ylabel=row_title[row_idx])

    plt.tight_layout()

plot([get_noisy_image(x_start, torch.tensor([t])) for t in [0, 50, 100, 150, 199]])

这意味着我们现在可以定义损失函数给定模型如下

def p_losses(denoise_model, x_start, t, noise=None, loss_type="l1"):
    if noise is None:
        noise = torch.randn_like(x_start)

    x_noisy = q_sample(x_start=x_start, t=t, noise=noise)
    predicted_noise = denoise_model(x_noisy, t)

    if loss_type == 'l1':
        loss = F.l1_loss(noise, predicted_noise)
    elif loss_type == 'l2':
        loss = F.mse_loss(noise, predicted_noise)
    elif loss_type == "huber":
        loss = F.smooth_l1_loss(noise, predicted_noise)
    else:
        raise NotImplementedError()

    return loss

噪声模型将是我们上面定义的U-Net。我们将在真实噪声和预测噪声之间使用Huber损失。

定义一个PyTorch Dataset + DataLoader

这里我们定义了一个常规的PyTorch数据集。该数据集仅由来自真实数据集的图像组成，如Fashion-MNIST, CIFAR-10或ImageNet，线性缩放到[1,1]。

每个图像被调整为相同的大小。有趣的是，图像也是随机水平翻转的。从论文中

我们在CIFAR10的训练中使用随机水平翻转;我们尝试了带和不带翻转的训练，发现翻转可以略微提高样本质量。

这里我们使用珞datassets库轻松地从hub加载Fashion MNIST数据集。该数据集由已经具有相同分辨率的图像组成，即28x28。

from datasets import load_dataset

# load dataset from the hub
dataset = load_dataset("fashion_mnist")
image_size = 28
channels = 1
batch_size = 128

接下来，我们定义一个函数，我们将在整个数据集上动态应用它。我们使用with_transform 功能。该函数只应用一些基本的图像预处理:随机水平翻转，重新缩放，最后使它们的值在[1,1]范围内。

from torchvision import transforms
from torch.utils.data import DataLoader

# define image transformations (e.g. using torchvision)
transform = Compose([
            transforms.RandomHorizontalFlip(),
            transforms.ToTensor(),
            transforms.Lambda(lambda t: (t * 2) - 1)
])

# define function
def transforms(examples):
   examples["pixel_values"] = [transform(image.convert("L")) for image in examples["image"]]
   del examples["image"]

   return examples

transformed_dataset = dataset.with_transform(transforms).remove_columns("label")

# create dataloader
dataloader = DataLoader(transformed_dataset["train"], batch_size=batch_size, shuffle=True)

batch = next(iter(dataloader))
print(batch.keys())

Sampling

由于我们将在训练期间从模型中采样(为了跟踪进度)，我们将在下面定义代码。本文将采样归纳为算法2

从扩散模型中生成新图像是通过逆转扩散过程来实现的:我们从$T$开始，从高斯分布中采样纯噪声，然后使用我们的神经网络逐渐去噪(使用它已经学习的条件概率)，直到我们在时间步长$t=0$时结束。如上所示，我们可以通过插入均值的重新参数化，使用我们的噪声预测器，得到一个去噪程度稍低的图像$x_{t-1}$。记住，方差是提前知道的。

理想情况下，我们最终得到的图像看起来像是来自真实的数据分布。

下面的代码实现了这一点。

@torch.no_grad()
def p_sample(model, x, t, t_index):
    betas_t = extract(betas, t, x.shape)
    sqrt_one_minus_alphas_cumprod_t = extract(
        sqrt_one_minus_alphas_cumprod, t, x.shape
    )
    sqrt_recip_alphas_t = extract(sqrt_recip_alphas, t, x.shape)
    
    # Equation 11 in the paper
    # Use our model (noise predictor) to predict the mean
    model_mean = sqrt_recip_alphas_t * (
        x - betas_t * model(x, t) / sqrt_one_minus_alphas_cumprod_t
    )

    if t_index == 0:
        return model_mean
    else:
        posterior_variance_t = extract(posterior_variance, t, x.shape)
        noise = torch.randn_like(x)
        # Algorithm 2 line 4:
        return model_mean + torch.sqrt(posterior_variance_t) * noise 

# Algorithm 2 (including returning all images)
@torch.no_grad()
def p_sample_loop(model, shape):
    device = next(model.parameters()).device

    b = shape[0]
    # start from pure noise (for each example in the batch)
    img = torch.randn(shape, device=device)
    imgs = []

    for i in tqdm(reversed(range(0, timesteps)), desc='sampling loop time step', total=timesteps):
        img = p_sample(model, img, torch.full((b,), i, device=device, dtype=torch.long), i)
        imgs.append(img.cpu().numpy())
    return imgs

@torch.no_grad()
def sample(model, image_size, batch_size=16, channels=3):
    return p_sample_loop(model, shape=(batch_size, channels, image_size, image_size))

注意，上面的代码是原始实现的简化版本。我们发现我们的简化(与论文中的算法2一致)与原始的、更复杂的实现(使用 clipping)一样有效。

训练模型

接下来，我们以常规的PyTorch方式训练模型。我们还定义了一些逻辑，使用上面定义的示例方法定期保存生成的图像。

from pathlib import Path

def num_to_groups(num, divisor):
    groups = num // divisor
    remainder = num % divisor
    arr = [divisor] * groups
    if remainder > 0:
        arr.append(remainder)
    return arr

results_folder = Path("./results")
results_folder.mkdir(exist_ok = True)
save_and_sample_every = 1000

下面，我们定义模型，并将其移动到GPU。我们还定义了一个标准优化器(Adam)。

from torch.optim import Adam

device = "cuda" if torch.cuda.is_available() else "cpu"

model = Unet(
    dim=image_size,
    channels=channels,
    dim_mults=(1, 2, 4,)
)
model.to(device)

optimizer = Adam(model.parameters(), lr=1e-3)

我们开始训练吧

from torchvision.utils import save_image

epochs = 6

for epoch in range(epochs):
    for step, batch in enumerate(dataloader):
      optimizer.zero_grad()

      batch_size = batch["pixel_values"].shape[0]
      batch = batch["pixel_values"].to(device)

      # Algorithm 1 line 3: sample t uniformally for every example in the batch
      t = torch.randint(0, timesteps, (batch_size,), device=device).long()

      loss = p_losses(model, batch, t, loss_type="huber")

      if step % 100 == 0:
        print("Loss:", loss.item())

      loss.backward()
      optimizer.step()

      # save generated images
      if step != 0 and step % save_and_sample_every == 0:
        milestone = step // save_and_sample_every
        batches = num_to_groups(4, batch_size)
        all_images_list = list(map(lambda n: sample(model, batch_size=n, channels=channels), batches))
        all_images = torch.cat(all_images_list, dim=0)
        all_images = (all_images + 1) * 0.5
        save_image(all_images, str(results_folder / f'sample-{milestone}.png'), nrow = 6)

Sampling (inference)

要从模型中抽样，我们可以使用上面定义的样本函数

# sample 64 images
samples = sample(model, image_size=image_size, batch_size=64, channels=channels)

# show a random one
random_index = 5
plt.imshow(samples[-1][random_index].reshape(image_size, image_size, channels), cmap="gray")

似乎这个模型能够生成一件漂亮的t恤!请记住，我们训练的数据集分辨率很低(28x28)。

我们还可以创建一个去噪过程的gif

import matplotlib.animation as animation

random_index = 53

fig = plt.figure()
ims = []
for i in range(timesteps):
    im = plt.imshow(samples[i][random_index].reshape(image_size, image_size, channels), cmap="gray", animated=True)
    ims.append([im])

animate = animation.ArtistAnimation(fig, ims, interval=50, blit=True, repeat_delay=1000)
animate.save('diffusion.gif')
plt.show()