（二）随机变量的数字特征：探索概率分布的关键指标

1. 随机变量的数学期望

1.1 离散型随机变量的数学期望

• 0-1分布

0-1分布是一种二值分布，表示事件发生与否的概率，通常用p表示成功的概率，1-p表示失败的概率。其数学期望为E(X) = p。

• 二项分布

二项分布描述了n次独立重复的二值试验，其中每次试验成功的概率为p。其数学期望为E(X) = np。

• 泊松分布

泊松分布适用于描述单位时间或空间内随机事件发生的次数，如电话呼叫、到达客户等。其数学期望为E(X) = λ，其中λ表示单位时间或空间内平均发生的次数。

• 几何分布

几何分布用于描述在n次独立重复的伯努利试验中首次成功发生的次数。其数学期望为E(X) = 1/p，其中p表示每次试验成功的概率。

1.2 连续型随机变量的数学期望

• 均匀分布

均匀分布在区间[a, b]内等可能地取任何值。其数学期望为E(X) = (a + b) / 2。

• 指数分布

指数分布描述了连续事件发生的时间间隔，其数学期望为E(X) = 1/λ，其中λ为事件发生率。

• 正态分布

正态分布是自然界中最常见的分布之一，其数学期望为E(X) = μ，其中μ为均值。

2. 随机变量函数的数学期望

2.1 一维随机变量函数的数学期望

假设我们有一个一维随机变量 X，以及一个实值函数 g(X)。一维随机变量函数 g(X) 的数学期望，通常表示为 E[g(X)]，是对该函数在随机变量 X 上的期望值。具体计算方法如下：

对于离散型随机变量 XX，数学期望 E[g(X)]E[g(X)] 的计算方法为：
E[g(X)]=x∑​g(x)P(X=x)

其中，∑x表示对所有可能的取值 x 求和，P(X=x) 是 X 等于 x 的概率质量函数。

对于连续型随机变量 X，数学期望 E[g(X)] 的计算方法为：
E[g(X)]=∫g(x)f(x)dx

其中，∫ 表示对所有可能的取值 x 进行积分，f(x) 是 X 的概率密度函数。

2.2 二维随机变量函数的数学期望

对于二维随机变量，我们可以考虑一个函数 g(X,Y)，其中 X 和 Y 是两个随机变量。二维随机变量函数 g(X,Y) 的数学期望，通常表示为 E[g(X,Y)]，是对该函数在随机变量 X 和 Y 上的期望值。具体计算方法如下：

对于离散型随机变量 X 和 Y，数学期望E[g(X,Y)] 的计算方法为：
E[g(X,Y)]=x∑​y∑​g(x,y)P(X=x,Y=y)

其中，∑x​ 和 ∑y​ 分别表示对所有可能的取值 x 和 y 求和，P(X=x,Y=y) 是联合概率质量函数。

对于连续型随机变量 X 和 Y，数学期望 E[g(X,Y)] 的计算方法为：
E[g(X,Y)]=∬g(x,y)f(x,y)dxdy

其中，∬ 表示对所有可能的取值 x和 y 进行二重积分，f(x,y) 是 X 和 Y 的联合概率密度函数。

3. 数学期望的性质

1. 线性性质：数学期望具有线性性质，即对于任意常数 aa 和 bb 以及随机变量 XX 和 YY，有以下公式：
   E(aX+bY)=aE(X)+bE(Y)E(aX+bY)=aE(X)+bE(Y)

2. 常数性质：如果 cc 是一个常数，那么对于任何随机变量 XX，都有：
   E©=cE©=c

3. 独立性质：如果 XX 和 YY 是独立的随机变量，那么它们的联合数学期望等于各自数学期望的乘积：
   E(XY)=E(X)E(Y)E(XY)=E(X)E(Y)

4. 非负性质：对于任何非负随机变量 XX，其数学期望也是非负的：
   如果 X≥0X≥0，则 E(X)≥0E(X)≥0

5. 单调性质：如果对于所有的样本点， XX 总是小于等于 YY，则 E(X)≤E(Y)E(X)≤E(Y)。

6. 凹凸性质：对于任意函数 g(X)g(X)，有以下凹凸性质：
   如果 g(X)g(X) 是凸函数，则 E[g(X)]≥g(E(X))E[g(X)]≥g(E(X))
   如果 g(X)g(X) 是凹函数，则 E[g(X)]≤g(E(X))E[g(X)]≤g(E(X))

7. 数学期望的绝对值性质：对于任何随机变量 XX，有：
   ∣E(X)∣≤E(∣X∣)∣E(X)∣≤E(∣X∣)

8. 常见分布的数学期望：对于特定的常见分布，数学期望具有相应的性质。例如，正态分布的数学期望等于其均值，指数分布的数学期望等于其倒数的平均，等等。

4. 方差的定义

方差是用来衡量随机变量数据分散程度的统计量。它衡量了随机变量的取值在其数学期望周围的离散程度。方差的定义如下：

对于一个随机变量 X，其数学期望为 E(X)，则它的方差 Var(X) 定义为：
Var(X)=E[(X−E(X))^2]

其中，X−E(X) 表示随机变量 XX 的每个取值与其数学期望 E(X) 之间的差距，然后将这些差距平方，再计算其数学期望。

方差的计算步骤如下：

• 对于每个随机变量 X 的取值 x，计算其与数学期望 E(X) 的差值：X−E(X)。
• 将每个差值平方：(X−E(X))^2。
• 对所有这些平方差值求期望值，即对所有可能的 x 进行加权平均。

方差表示了随机变量数据分布的离散程度。如果方差较小，意味着数据点较接近数学期望，分布较集中；如果方差较大，说明数据点相对较远离数学期望，分布较分散。

5. 方差的性质

方差（Variance）是一个重要的统计量，用于衡量随机变量的离散程度。它具有一些重要的性质，这些性质在统计分析和概率论中经常用于推导和计算。以下是方差的主要性质：

1. 非负性：方差始终是非负数。
   Var(X)≥0

2. 方差与数学期望的关系：方差可以通过数学期望来表示。
   Var(X)=E[(X−E(X))^2]

3. 常数倍性质：如果 a 是一个常数，那么随机变量 aX 的方差是 a^2 乘以 X 的方差。
   Var(aX)=a^2Var(X)

4. 加法性质：对于两个随机变量 X 和 Y，它们的和 X+Y 的方差等于它们各自方差的和，加上它们的协方差（如果有）。
   Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)

5. 常数的方差为零：对于任何常数 c，Var©=0。
   Var©=0

6. 独立性质：如果随机变量 X 和 Y 独立，它们的和 X+Y 的方差等于它们各自的方差之和。
   如果 X 和 Y 独立，那么 Var(X+Y)=Var(X)+Var(Y)

7. 常见分布的方差：对于某些常见的概率分布，方差具有特定的表达式，例如：
   对于二项分布：Var(X)=np(1−p)，其中 n 是试验次数，p 是成功的概率。
   对于泊松分布：Var(X)=λ，其中 λ 是泊松分布的均值和方差。
   对于正态分布：Var(X)=σ^2，其中 σ 是标准差。

8. 方差的非负性证明：方差的非负性是方差的基本性质，可以通过方差的定义以及平方的非负性证明得出。证明中使用了 E[(X−E(X))^2] 的平方永远是非负的性质。

分布	期望	方差
0-1分布	p	p(1-p)
二项分布	np	np(1-p)
泊松分布	λ	λ
几何分布	1/p	(1-p)/p^2
均匀分布	(a+b)/2	(b-a)^2/12
指数分布	1/λ	1/λ^2
正态分布	μ	σ^2

6. 协方差与相关系数

协方差（Covariance）：

协方差用于衡量两个随机变量的变化趋势是否一致。具体而言，协方差测量了两个随机变量（假设为 X 和 Y）之间的线性关系。协方差的定义如下：

对于两个随机变量 X 和 Y，其协方差 Cov(X,Y) 定义为：

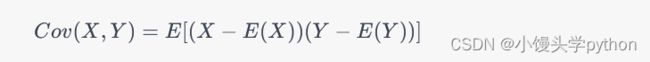
其中，E(X)和 E(Y) 分别是 X 和 Y 的数学期望。
协方差的性质如下：

• 如果 X 和 Y 之间存在正相关关系（即一个变量增加，另一个也增加），则协方差为正数。
• 如果 X 和 Y 之间存在负相关关系（即一个变量增加，另一个减少），则协方差为负数。
• 如果 X 和 Y 之间没有线性关系，协方差可能接近于零，但不能得出它们之间没有关系的结论。

然而，协方差的取值范围没有上限或下限，因此很难对其大小进行直观解释。为了更好地理解两个随机变量之间的关系，通常使用相关系数。

相关系数（Correlation Coefficient）：

相关系数是协方差的标准化版本，它将协方差除以两个随机变量的标准差，从而使其取值范围在 -1 到 1 之间。相关系数表示了两个随机变量之间的线性关系强度和方向。最常见的相关系数是皮尔逊相关系数（Pearson Correlation Coefficient）。

皮尔逊相关系数（ρρ）的定义如下：

其中，Cov(X,Y) 是 X 和 Y 的协方差，σX​ 和 σY​ 分别是 X 和 Y 的标准差。

皮尔逊相关系数的性质如下：

• ρ 的取值范围在 -1 到 1 之间。当 ρ=1 时，表示完全正相关；当 ρ=−1 时，表示完全负相关；当 ρ=0 时，表示没有线性关系。
• ρ 的符号表示变量之间的关系方向。正值表示正相关，负值表示负相关。
• 皮尔逊相关系数对线性关系敏感，如果关系是非线性的，它可能无法准确捕捉到这种关系。

总之，协方差和相关系数是用于描述随机变量之间关系的重要工具。协方差衡量了变量之间的总体关联性，而相关系数则在协方差的基础上提供了标准化的度量，更容易理解和解释。在数据分析中，它们通常用于研究变量之间的关系，特别是在回归分析和多元统计中。

挑战与创造都是很痛苦的，但是很充实。