代码随想录算法训练营第16天 | 二叉树part03：● 104.二叉树最大深度 559.n叉树最大深度● 111.二叉树最小深度● 222.完全二叉树节点个数

104 二叉树最大深度

几种方法

1 dfs 递归 前中后序模板法 是直接求depth

一些发现：if (node->left ! = nullptr)可以直接写做 if (node->left)；可以在class里统一写一个var就不用用ref传来传去了

class Solution {
public:
    int result;
    void getdepth(TreeNode* node, int depth) {
        result = depth > result ? depth : result; // 中
        //if (node->left == NULL && node->right == NULL) return ;
        if (node->left) getdepth(node->left, depth + 1);
        if (node->right) getdepth(node->right, depth + 1);
    }
    int maxDepth(TreeNode* root) {
        result = 0;
        if (root == 0) return result;
        getdepth(root, 1);
        return result;
    }
};

新学到的一点是：才意识到右边是左边的详细逻辑，就是思考上要考虑到回溯的过程

2 dfs 递归后序另一种写法是通过求root的高度来求树的最大深度

• 节点深度：root到node的最长简单路径边的条数或者节点数（取决于深度从0开始还是从1开始）
• 节点高度：node到leaf的最长简单路径边的条数或者节点数（取决于高度从0开始还是从1开始）

root高度就是二叉树的最大深度

class solution {
public:
    int getdepth(TreeNode* node) {
        if (node == NULL) return 0;
        int leftdepth = getdepth(node->left);       // 左
        int rightdepth = getdepth(node->right);     // 右
        int depth = 1 + max(leftdepth, rightdepth); // 中
        return depth;
    }
    int maxDepth(TreeNode* root) {
        return getdepth(root);
    }
};

3 迭代法的话适合bfs那种层序的（不是dfs的迭代），直接套模板

559.n叉树的最大深度

也是分为递归dfs（只有一种了）和bfs层序遍历

dfs：

void order(Node* node, int depth, int&max){
        if(node==nullptr) return;
        vector clist=node->children;
        max=std::max(max,depth);
        for(auto ele:clist){
            order(ele, depth+1, max);
        }

    }
    int maxDepth(Node* root) {
        int depth=1;
        int max=0;
        order(root,depth,max);
        return max;
    }

更简洁的：

int maxDepth(Node* root) {
        if (root == 0) return 0;
        int depth = 0;
        for (int i = 0; i < root->children.size(); i++) {
            depth = max (depth, maxDepth(root->children[i]));
        }
        return depth + 1;
    }

bfs迭代

nt maxDepth(Node* root) {
        queue que;
        if (root != NULL) que.push(root);
        int depth = 0;
        while (!que.empty()) {
            int size = que.size();
            depth++; // 记录深度
            for (int i = 0; i < size; i++) {
                Node* node = que.front();
                que.pop();
                for (int j = 0; j < node->children.size(); j++) {
                    if (node->children[j]) que.push(node->children[j]);
                }
            }
        }
        return depth;
    }

111 二叉树最小深度

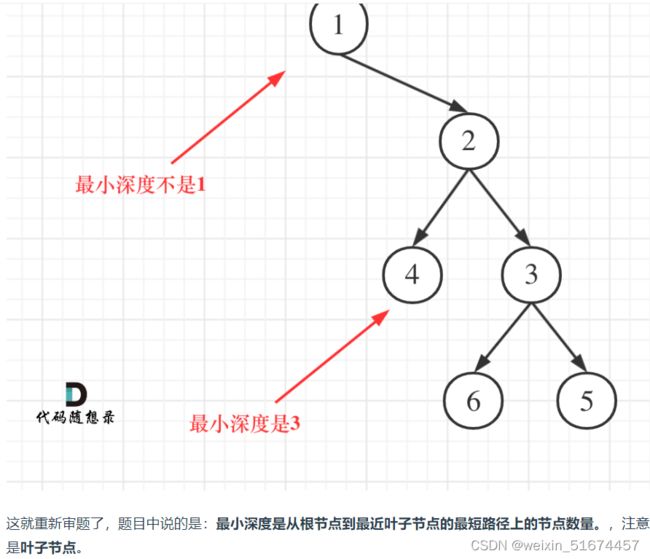
易错点：注意对最小深度的定义

 本题关键：左右孩子都为空的节点才是叶子节点，才能算一个path的结束

方法包括：层序遍历的迭代（走到第一个叶子节点就可得出答案退出了），dfs模板的前中后序（直接算depth），和通过算高度的后序dfs 【和104一样的 对应的这些方法】

模板和迭代在上一篇写了这里就不写了，后序求高度写一下：

 int minDepth(TreeNode* root) {
        if (root == NULL) return 0;
        if (root->left == NULL && root->right != NULL) {
            return 1 + minDepth(root->right);
        }
        if (root->left != NULL && root->right == NULL) {
            return 1 + minDepth(root->left);
        }
        return 1 + min(minDepth(root->left), minDepth(root->right));
    }

222 完全二叉树节点的个数

思路1：直接按照普通二叉树做

层序遍历的迭代：直接套模板

int countNodes(TreeNode* root) {
        queue que;
        if (root != NULL) que.push(root);
        int result = 0;
        while (!que.empty()) {
            int size = que.size();
            for (int i = 0; i < size; i++) {
                TreeNode* node = que.front();
                que.pop();
                result++;   
                if (node->left) que.push(node->left);
                if (node->right) que.push(node->right);
            }
        }
        return result;
    }

前中后序递归：

void order(TreeNode* node, int& cnt){
        if(node==nullptr) return;
        cnt++;
        if(node->left!=nullptr) order(node->left,cnt);
        if(node->right!=nullptr) order(node->right,cnt);

    }
    int countNodes(TreeNode* root) {
        int cnt=0;
        order(root,cnt);
        return cnt;
    }

后序递归：

int getNodesNum(TreeNode* cur) {
        if (cur == NULL) return 0;
        int leftNum = getNodesNum(cur->left);      // 左
        int rightNum = getNodesNum(cur->right);    // 右
        int treeNum = leftNum + rightNum + 1;      // 中
        return treeNum;
    }
int countNodes(TreeNode* root) {
        return getNodesNum(root);
    }

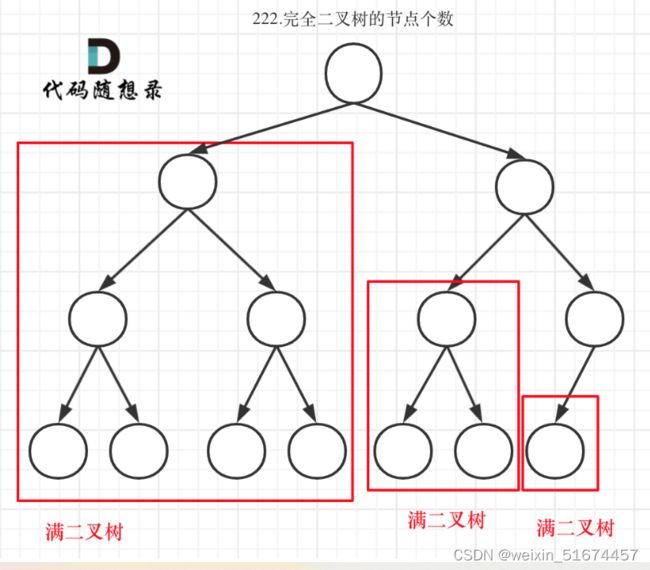
思路二：用完全二叉树的性质来做

完全二叉树只有两种情况，1：满二叉树，2：最后一层叶子节点没有满。

1，可以直接用 2^depth - 1 来计算，注意这里根节点深度为1。先求出depth即可

2，分别递归左/右孩子，递归到某深度一定会有左/右孩子为满二叉树，然后依照情况1来计算。

判断一个左子树或者右子树是不是满二叉树呢？ 在完全二叉树中，如果递归向左遍历的深度等于递归向右遍历的深度，那说明就是满二叉树

int countNodes(TreeNode* root) {
        if (root == nullptr) return 0;
        TreeNode* left = root->left;
        TreeNode* right = root->right;
        int leftDepth = 1, rightDepth = 1; //注意下面计算node个数一定深度要从1开始
        while (left) {  
            left = left->left;
            leftDepth++;
        }
        while (right) { 
            right = right->right;
            rightDepth++;
        }
        if (leftDepth == rightDepth) return pow(2,leftDepth)-1;
            
        
        return countNodes(root->left) + countNodes(root->right) + 1;
    }

另一种写法，先初始化为0，然后 写return (2 << leftDepth) - 1; // 注意(2<<1) 相当于2^2，返回满足满二叉树的子树节点数量