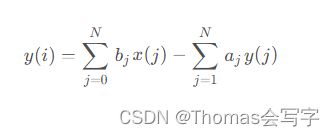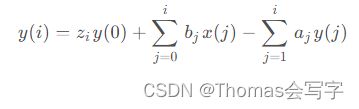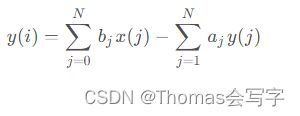Matlab的filtfilt函数解析

 

目录

0.前言

1.filtfilt函数的解析

1.1 主要流程

1.2 边界的延拓

1.3 边界效应的优化

1.4 滤波器系数获取

2.C++实现及对比

2.1 C++实现

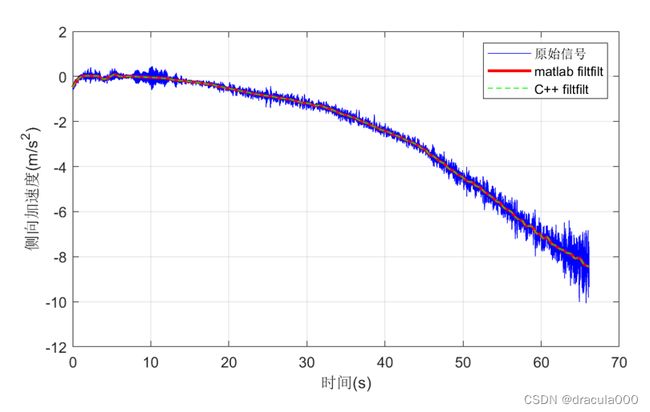
滤波结果对比

参考文献

补充 Zi 计算

---

0.前言

传统滤波（如Matlab的filter函数）会造成信号的延迟，延迟程度与滤波器的阶次有关，为了解决延迟问题，Matlab提供了filtfilt函数，该方法一般称为零相位滤波或双向滤波。
本文的目的是对Matlab中的filtfilt函数原理进行解析，并在C++中实现。

1.filtfilt函数的解析

参考Matlab中的filter函数和filtfilt函数，对零相位滤波原理进行解析。

1.1 主要流程

零相位滤波的主要流程如下：

1.2 边界的延拓

为了改善边界效应，对原始信号数据进行延拓，即在首尾处增加数据点。
对于N阶的滤波器，单边延拓的数据长度为nfact =3* N。
延拓数据的计算方式如下：

1.3 边界效应的优化

滤波可以通过差分的方式实现，网上很多资料给出的计算公式如下：

上述公式从i≥N开始计算起，对于i 在Matlab中为了进一步优化边界效应，对滤波的算法进行了扩展，具体算法如下：
对于阶滤波器，滤波系数分别为和， 为边界优化系数， 为原始信号， 为滤波后的结果。
当i

当i≥N时，

1.4 滤波器系数获取

对于阶滤波器，滤波系数和均为N+1维，可通过Matlab的滤波器构造函数获得（如butter函数）。
边界优化系数zi为N维，通过a和b计算，计算方法如下：

nfilt = max(nb,na);
rows = [1:nfilt-1, 2:nfilt-1, 1:nfilt-2];
cols = [ones(1,nfilt-1), 2:nfilt-1, 2:nfilt-1];
vals = [1+a(2), a(3:nfilt)', ones(1,nfilt-2), -ones(1,nfilt-2)];
rhs  = b(2:nfilt) - b(1)*a(2:nfilt);
zi   = sparse(rows,cols,vals) \ rhs;
% The non-sparse solution to zi may be computed using:
%      zi = ( eye(nfilt-1) - [-a(2:nfilt), [eye(nfilt-2); ...
%                                           zeros(1,nfilt-2)]] ) \ ...
%          ( b(2:nfilt) - b(1)*a(2:nfilt) );

2.C++实现及对比

2.1 C++实现

.h文件

#pragma once
struct stFilterCoeff
{
	int len;

	double *a;
	double *b;
	double *zi;
};

template
T getMax(T& a, T& b);

template
T getMin(T& a, T& b);

template
int getLength(T& a);

const char* writeToTxt(const char* name, double *datas, int lenN);

class FiltFilt //零相位滤波器
{
public:
	FiltFilt(const int alen, const int blen, double *a, double *b, double *zi);
	void filtfiltData(const double *sig, double *sout, const int data_len);

private:
	stFilterCoeff myfilter;
	void filtData(const double *sig, double *sout, const int data_len);
	int signalExtend(const double *sig, double *sout, const int data_len, const int nfact);
	void dataRollover(const double *sig, double *sout, const int data_len);

};

.c文件

#include "mFiltFilt.h"
FiltFilt::FiltFilt(const int alen, const int blen, double *a, double *b, double *zi)
{
	myfilter.len = getMax(alen, blen); //使a和b同维度

	myfilter.a = new double[myfilter.len];
	myfilter.b = new double[myfilter.len];
	myfilter.zi = new double[myfilter.len - 1];

	for (int i = 0; i < myfilter.len; i++)
	{
		myfilter.a[i] = a[i];
		myfilter.b[i] = b[i];
	}
	for (int i = 0; i < myfilter.len-1; i++)
	{
		myfilter.zi[i] = zi[i];

	}
}

void FiltFilt::filtfiltData(const double *sig, double *sout, const int data_len)
{
	// 零相位滤波
	int N = myfilter.len;
	int nfact = 3 * (N - 1);

	int len_ext = data_len + 2 * nfact; //信号延拓后的长度

	double *s_ext = new double[len_ext]; // 延拓后的信号（待滤波）
	double *s_fft = new double[len_ext]; // 滤波后的信号

	// 延拓 sig -> s_ext
	signalExtend(sig, s_ext, data_len, nfact); 
	// 滤波 s_ext -> s_fft
	filtData(s_ext, s_fft, len_ext);
	// 翻转 s_fft -> s_ext
	dataRollover(s_fft, s_ext, len_ext);
	// 滤波 s_ext -> s_fft
	filtData(s_ext, s_fft, len_ext);
	// 翻转 s_fft -> s_ext
	dataRollover(s_fft, s_ext, len_ext);
	// 输出 s_ext -> sout
	for (int i = 0; i < data_len; i++)
	{
		sout[i] = s_ext[i + nfact];
	}
}

void FiltFilt::filtData(const double *sig, double *sout, const int data_len)
{
	int N = myfilter.len;
	for (int i = 0; i < data_len; i++)
	{
		sout[i] = sig[i];
		//printf("sig[%d]=%f\n", i, sig[i]);
	}
	for (int i = 0; i < N-1; i++) 
	{
		double tmp = myfilter.zi[i] * sig[0];
		for (int j = 0; j < i+1; j++)
		{
			tmp += myfilter.b[j] * sig[i - j];
		}
		for (int j = 1; j < i+1; j++)
		{
			tmp -= myfilter.a[j] * sout[i - j];
		}
		sout[i] = tmp;
	}
	for (int i = N - 1; i < data_len; i++)
	{
		double tmp = 0;
		for (int j = 0; j < myfilter.len; j++)
		{
			tmp += myfilter.b[j] * sig[i - j];
		}
		for (int j = 1; j < myfilter.len; j++)
		{
			tmp -= myfilter.a[j] * sout[i - j];
		}
		sout[i] = tmp;
		//printf("out[%d]=%f\n",i, tmp);
	}
}

int FiltFilt::signalExtend(const double *sig, double *sout, const int data_len, const int nfact)
{
	// 数据延拓
	int head_extN = nfact;
	int tail_extN = nfact;
	int data_extN = data_len + head_extN + tail_extN;
	double data0 = 2*sig[0];
	double data1 = 2*sig[data_len-1];
	for (int i = 0; i < head_extN; i++)
	{
		sout[i] = data0-sig[head_extN - i];
	}
	for (int i = head_extN; i < data_len + head_extN; i++)
	{
		sout[i] = sig[i - head_extN];
	}
	for (size_t i = data_len + head_extN; i < data_extN; i++)
	{
		sout[i] = data1-sig[data_len + head_extN - i + data_len - 2];
	}
	
	return data_extN;

}

void FiltFilt::dataRollover(const double *sig, double *sout, const int data_len)
{
	// 数据翻转
	for (int i = 0; i < data_len; i++)
	{
		//printf("sig[%d]=%f\n", i, sig[i]);
		sout[data_len - i - 1] = sig[i];
	}
}

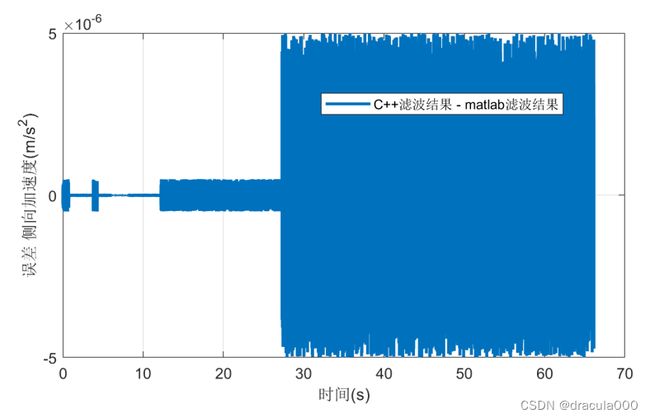
滤波结果对比

使用相同的滤波器，C++的滤波结果与Matlab的filtfilt函数滤波结果对比如下：

参考文献

[1] 零相位(双边)滤波器设计–C++/Matlab

补充 Zi 计算

// a b 就是分子分母系数
double[] ComputeZi()
{
    int nLen = a.Length - 1;
    Matrix ma = Matrix.Zeros(nLen, nLen);
    Matrix mb = Matrix.Zeros(nLen, 1);

    ma[0, 0] = a[1] + 1;
    for (int i = 1; i < nLen; i++)
    {
        ma[i, 0] = a[i + 1];
        ma[i, i] = 1;
        ma[i - 1, i] = -1;
    }
    for (int i = 0; i < nLen; i++)
    {
        mb[i, 0] = b[i + 1] - a[i + 1] * b[0];
    }
    Matrix mz = ma.Solve(mb);  // 基于 Matrix LU 分解的矩阵求解
    return mz.ToArray();
}