【论文笔记】NeRF-RPN: A general framework for object detection in NeRFs
原文链接:https://arxiv.org/abs/2211.11646
1. 引言
NeRF模型能直接从给定的RGB图像和相机姿态学习3D场景的NeRF表达。本文提出NeRF-RPN,使用从NeRF模型提取的辐射场和密度,直接生成边界框提案。
3. 方法
如图所示,本文的方法有两个组成部分,特征提取器(从NeRF采样的辐射和密度网格)和RPN头(生成物体提案)。
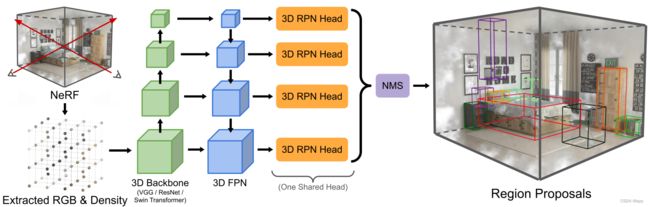
3.1 从NeRF输入采样
第一步是均匀采样NeRF模型的辐射和密度场,建立特征体积网格。体积网格的分辨率与各维度范围成正比,从而保证物体的长宽比。对使用RGB作为辐射表达的NeRF模型,本文从NeRF训练时使用的视图集合中采样并平均结果。若相机姿态未知,则从球上均匀采样方向。通常来说,给定样本 ( r , g , b , α ) (r,g,b,\alpha) (r,g,b,α),其中 ( r , g , b ) (r,g,b) (r,g,b)为平均后的辐射, α \alpha α是从密度转换得到的: α = clip ( 1 − exp ( − σ δ ) , 0 , 1 ) \alpha=\text{clip}(1-\exp(-\sigma\delta),0,1) α=clip(1−exp(−σδ),0,1)其中 δ = 0.01 \delta=0.01 δ=0.01是预设的距离。对使用球面谐波或其他基函数表达辐射的NeRF,可以根据下游任务,使用RGB值或基函数的系数作为辐射信息。
3.2 特征提取器
考虑到不同大小的物体和不同尺度的场景,本文特征提取器中使用FPN输出特征金字塔。
3.3 3D区域提案网络
3D RPN以特征金字塔为输入,输出一组有朝向的边界框及其对应的分数。本文实验了两种RPN:基于锚框的和无需锚框的,如下图所示。
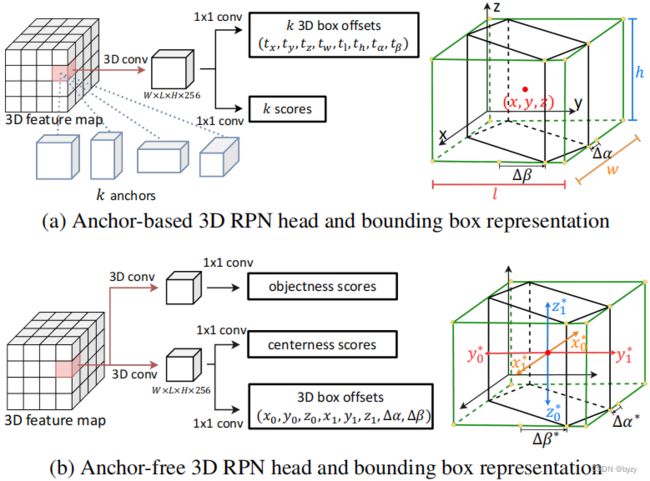
基于锚框的RPN:本文在特征金字塔的各层放置不同长宽比和尺寸的3D锚框,使用卷积预测各锚框内物体的偏移量和分数。各层之间的卷积共享权重。边界框偏移量 t = ( t x , t y , t z , t w , t l , t h , t α , t β ) t=(t_x,t_y,t_z,t_w,t_l,t_h,t_\alpha,t_\beta) t=(tx,ty,tz,tw,tl,th,tα,tβ)的回归目标被定义如下: t x = ( x − x a ) / w a , t y = ( y − y a ) / l a , t z = ( z − z a ) / h a t w = log ( w / w a ) , t l = log ( l / l a ) , t h = log ( h / h a ) t α = Δ α / w , t β = Δ β / l t_x=(x-x_a)/w_a,t_y=(y-y_a)/l_a,t_z=(z-z_a)/h_a\\t_w=\log(w/w_a),t_l=\log(l/l_a),t_h=\log(h/h_a)\\t_\alpha=\Delta\alpha/w,t_\beta=\Delta\beta/l tx=(x−xa)/wa,ty=(y−ya)/la,tz=(z−za)/hatw=log(w/wa),tl=log(l/la),th=log(h/ha)tα=Δα/w,tβ=Δβ/l其中 x , y , z , w , l , h , α , β x,y,z,w,l,h,\alpha,\beta x,y,z,w,l,h,α,β为真实边界框参数, x a , y a , z a , w a , l a , h a x_a,y_a,z_a,w_a,l_a,h_a xa,ya,za,wa,la,ha为锚框参数。
当某提案与任一真实边界框的IoU大于0.35时,或在所有提案中与某一真实边界框的IoU最大时,该提案被标记为正;非正提案中,与所有真实边界框的IoU均小于0.2的被标记为负。其余提案不参与损失函数的计算。损失函数与Faster-RCNN类似,分类使用二元交叉熵损失,回归使用smoothL1损失(仅对正锚框计算): L = 1 N ∑ i L c l s ( p i , p i ∗ ) + λ N p o s ∑ i p i ∗ L r e g ( t i , t i ∗ ) L=\frac{1}{N}\sum_iL_{cls}(p_i,p_i^*)+\frac{\lambda}{N_{pos}}\sum_ip^*_iL_{reg}(t_i,t_i^*) L=N1i∑Lcls(pi,pi∗)+Nposλi∑pi∗Lreg(ti,ti∗)后处理前会将提案转化为长方体。
无需锚框的RPN:类似FCOS,预测分数 p p p、中心性 c c c和边界框偏移量 t = ( x 0 , y 0 , z 0 , x 1 , y 1 , z 1 , Δ α , Δ β ) t=(x_0,y_0,z_0,x_1,y_1,z_1,\Delta\alpha,\Delta\beta) t=(x0,y0,z0,x1,y1,z1,Δα,Δβ)。回归目标被定义为: x 0 ∗ = x − x 0 ( i ) , x 1 ∗ = x 1 ( i ) − x , y 0 ∗ = y − y 0 ( i ) , y 1 ∗ = y 1 ( i ) − y , z 0 ∗ = z − z 0 ( i ) , z 1 ∗ = z 1 ( i ) − z Δ α ∗ = v x ( i ) − x , Δ β ∗ = v y ( i ) − y x_0^*=x-x_0^{(i)},x_1^*=x_1^{(i)}-x,y_0^*=y-y_0^{(i)},y_1^*=y_1^{(i)}-y,z_0^*=z-z_0^{(i)},z_1^*=z_1^{(i)}-z\\\Delta\alpha^*=v_x^{(i)}-x,\Delta\beta^*=v_y^{(i)}-y x0∗=x−x0(i),x1∗=x1(i)−x,y0∗=y−y0(i),y1∗=y1(i)−y,z0∗=z−z0(i),z1∗=z1(i)−zΔα∗=vx(i)−x,Δβ∗=vy(i)−y其中 x , y , z x,y,z x,y,z表示体素位置,上标 ( i ) (i) (i)表示真实边界框,下标0和下标1代表该真实轴对齐边界框在该维度上的下界和上界。 v x ( i ) v_x^{(i)} vx(i)表示真实边界框在 x y xy xy平面投影中最上方顶点的 x x x坐标, v y ( i ) v_y^{(i)} vy(i)表示真实边界框在BEV投影中最右方顶点的 y y y坐标,如上图所示。中心性的真实值为 c ∗ = min ( x 0 ∗ , x 1 ∗ ) max ( x 0 ∗ , x 1 ∗ ) × min ( y 0 ∗ , y 1 ∗ ) max ( y 0 ∗ , y 1 ∗ ) × min ( z 0 ∗ , z 1 ∗ ) max ( z 0 ∗ , z 1 ∗ ) c^*=\sqrt{\frac{\min(x^*_0,x^*_1)}{\max(x^*_0,x^*_1)}\times\frac{\min(y^*_0,y^*_1)}{\max(y^*_0,y^*_1)}\times\frac{\min(z^*_0,z^*_1)}{\max(z^*_0,z^*_1)}} c∗=max(x0∗,x1∗)min(x0∗,x1∗)×max(y0∗,y1∗)min(y0∗,y1∗)×max(z0∗,z1∗)min(z0∗,z1∗)总损失为 L i = 1 N ∑ i L c l s ( p i , p i ∗ ) + λ N p o s ∑ i p i ∗ L r e g ( t i , t i ∗ ) + 1 N p o s ∑ i p i ∗ L c t r ( c i , c i ∗ ) L_i=\frac{1}{N}\sum_iL_{cls}(p_i,p_i^*)+\frac{\lambda}{N_{pos}}\sum_ip^*_iL_{reg}(t_i,t_i^*)+\frac{1}{N_{pos}}\sum_ip^*_iL_{ctr}(c_i,c_i^*) Li=N1i∑Lcls(pi,pi∗)+Nposλi∑pi∗Lreg(ti,ti∗)+Npos1i∑pi∗Lctr(ci,ci∗)其中分类损失为focal损失,回归损失为旋转边界框的IoU损失,中心性损失为二元交叉熵损失。 p i ∗ ∈ { 0 , 1 } p_i^*\in\{0,1\} pi∗∈{0,1}为体素真实标签,由FCOS中的中心采样和多级预测过程确定。 N p o s N_{pos} Npos为 p i ∗ = 1 p^*_i=1 pi∗=1的体素数。后处理前同样会将提案转化为长方体。
3.4 额外损失函数
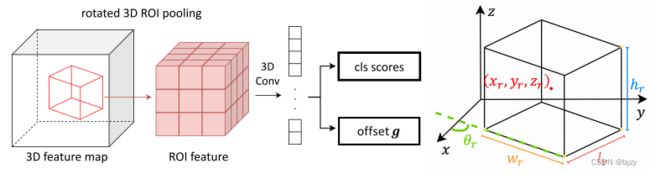
物体分类:虽然NeRF-RPN主要目标是获取高召回率,但有时候低FP率也很重要。本文加入二元分类网络实现前景/背景分割,输入RPN产生的感兴趣区RoI和特征提取器输出的特征金字塔,输出分类分数和RoI的细化偏移量,如上图所示。本文参考Oriented RPN,通过旋转RoI池化,为每个提案 ( x r , y r , z r , w r , l r , h r , θ r ) (x_r,y_r,z_r,w_r,l_r,h_r,\theta_r) (xr,yr,zr,wr,lr,hr,θr)提取具有旋转不变性的特征。首先,放大边界框并划分为特征体积网格,然后使用三线性插值计算每个网格的值,输入到池化层中,得到 N × 3 × 3 × 3 N\times3\times3\times3 N×3×3×3大小,输入分类和回归分支。此处的边界框偏移量 g = ( g x , g y , g z , g w , g l , g h , g θ ) g=(g_x,g_y,g_z,g_w,g_l,g_h,g_\theta) g=(gx,gy,gz,gw,gl,gh,gθ)被定义为: g x = ( ( x − x r ) cos θ r + ( y − y r ) sin θ r ) / w r , g y = ( ( y − y r ) cos θ r − ( x − x r ) sin θ r ) / l r , g z = ( z − z r ) / h r g w = log ( w / w r ) , g l = log ( l / l r ) , g h = log ( h / h r ) , g θ = ( θ − θ r ) / 2 π g_x=((x-x_r)\cos\theta_r+(y-y_r)\sin\theta_r)/w_r,g_y=((y-y_r)\cos\theta_r-(x-x_r)\sin\theta_r)/l_r,g_z=(z-z_r)/h_r\\g_w=\log(w/w_r),g_l=\log(l/l_r),g_h=\log(h/h_r),g_\theta=(\theta-\theta_r)/2\pi gx=((x−xr)cosθr+(y−yr)sinθr)/wr,gy=((y−yr)cosθr−(x−xr)sinθr)/lr,gz=(z−zr)/hrgw=log(w/wr),gl=log(l/lr),gh=log(h/hr),gθ=(θ−θr)/2π与任一真实边界框的IoU大于0.25的RoI被标记为物体,其余为非物体。损失函数与基于锚框的RPN一节类似,只有边界框偏移量被替换为 g , g ∗ g,g^* g,g∗。
2D投影损失:将3D边界框坐标 b i = ( x i , y i , z i ) b_i=(x_i,y_i,z_i) bi=(xi,yi,zi)投影到2D b i ′ = ( x i ′ , y i ′ ) b'_i=(x'_i,y'_i) bi′=(xi′,yi′),得到2D投影损失: L 2 d p r o j = 1 N c a m N b o x L r e g ( b i ′ , b i ′ ∗ ) L_{2d\ proj}=\frac{1}{N_{cam}N_{box}}L_{reg}(b'_i,{b'_i}^*) L2d proj=NcamNbox1Lreg(bi′,bi′∗)
5. 实验
5.1 训练&测试
训练:训练时输入场景被随机沿 x , y x,y x,y轴翻转和沿 z z z轴旋转 π / 2 \pi/2 π/2角。此外,场景也会随机沿 z z z轴再旋转一个小角度。对于基于锚框的RPN,每次随机采样256个锚框(正负比为1:1)进行损失计算。
测试:首先过滤场景外的边界框,然后为每个特征尺度选择2500个提案进行非最大抑制后,选择分数最高的2500个提案。
5.2 消融研究
主干和颈部:固定主干和颈部后,无需锚框的RPN有更好的性能,因为中心性预测能抑制那些较远的提案,且锚框固定的长宽比和尺寸限制其对尺寸不一物体的检测。
NeRF采样策略:NeRF的密度场是与视图无关的,而辐射场是与视图方向相关的,有各种编码方式。在补充材料中的实验表明,仅使用密度是最佳策略。
回归损失:使用IoU损失、DIoU损失以及其作用于带朝向边界框的变体进行实验,表明IoU损失能有更好的性能。
5.3 结果
实验表明,质量较差的NeRF重建会严重影响边界框预测。
应用:场景编辑。给定NeRF-RPN输出的提案,可以对NeRF场景进行编辑,如在渲染时设置提案内的密度为0。
补充材料
2. 对NeRF采样策略的消融研究
为探究NeRF视图相关的辐射信息对检测性能的影响,本文实验了下列采样方式:
- 仅使用密度;
- 使用固定的18个视图的平均辐射 + 密度;
- 使用训练时所有相机视图的平均辐射 + 密度;
- 在3的基础上,只选择视锥内包含采样点的训练视图;
- 使用最高3阶的球面谐波(SH)系数(SH函数是从球面上的300个方向均匀采样辐射得到的) + 密度。
实验表明,1的性能最优,这表明辐射信息会影响性能。
3. 物体分类
实验表明,使用物体分类损失会使性能下降。这可能是特征体积网格的分辨率有限,旋转插值会导致高重采样误差。但对于某些需要RoI特征的下游任务而言,物体分类损失仍可能是有用的。
4. 2D投影
实验表明,3D监督已经提供足够信息,使用2D监督不能提高性能。但当3D监督不存在时,2D投影损失仍可能有用。