矩阵乘法的应用
论文1 -> 俞华程《矩阵乘法在信息学中的应用》
二、题目
描述:求矩阵A^k的主对角线元素和 (mod 9973).
PS: 入门题[二分求矩阵幂]
 代码
代码
#include
<
stdio.h
>
#include
<
string
.h
>
#define
NL 10
#define
MD 9973
struct
Matrix {
int
v[NL][NL];
Matrix () {
memset(v,
0
,
sizeof
(v));
}
//
矩阵相乘
void
multiply(Matrix m,
int
n) {
Matrix m1;
for
(
int
i
=
0
; i
<
n; i
++
) {
for
(
int
j
=
0
; j
<
n; j
++
) {
for
(
int
k
=
0
; k
<
n; k
++
) {
m1.v[i][j]
+=
v[i][k]
*
m.v[k][j];
if
(m1.v[i][j]
>=
MD) m1.v[i][j]
%=
MD;
}
}
}
for
(
int
i
=
0
; i
<
n; i
++
) {
for
(
int
j
=
0
; j
<
n; j
++
)
v[i][j]
=
m1.v[i][j];
}
}
void
print(
int
n) {
for
(
int
i
=
0
; i
<
n; i
++
) {
for
(
int
j
=
0
; j
<
n; j
++
)
printf(
"
%d
"
, v[i][j]);
printf(
"
\n
"
);
}
}
};
int
main()
{
//
freopen("data.in", "r", stdin);
//
freopen("data.out", "w", stdout);
int
t;
int
n, k, k0;
scanf(
"
%d
"
,
&
t);
while
(t
--
) {
scanf(
"
%d%d
"
,
&
n,
&
k);
Matrix m0, m1;
for
(
int
i
=
0
; i
<
n; i
++
) {
for
(
int
j
=
0
; j
<
n; j
++
)
scanf(
"
%d
"
,
&
m0.v[i][j]);
}
m1
=
m0;
/*
二分求矩阵幂
*/
k
--
;
while
(k
>
0
) {
if
(k
&
1
) m1.multiply(m0,n);
m0.multiply(m0,n);
k
=
k
>>
1
;
}
int
ans
=
0
;
for
(
int
i
=
0
; i
<
n; i
++
) {
ans
+=
m1.v[i][i];
ans
%=
MD;
}
printf(
"
%d\n
"
, ans);
}
return
0
;
}
描述:
If x < 10, f(x) = x
If x >= 10, f(x) = a0 * f(x-1) + a1 * f(x-2) + a2 * f(x-3) + …… + a9 * f(x-10)
构造递推矩阵:
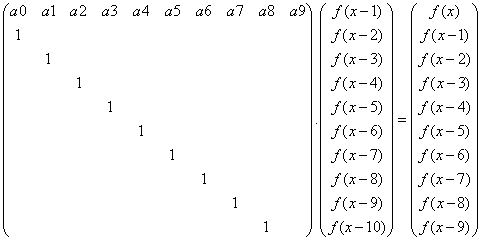
 代码
代码
#include
<
stdio.h
>
#include
<
string
.h
>
#define
NL 10
#define
FOR(i,k,n) for(i=k;i<n;i++)
int
md;
struct
Matrix {
int
v[NL][NL];
Matrix() {
memset(v,
0
,
sizeof
(v));
}
void
Multiply(Matrix m) {
int
i, j, k;
Matrix m1;
FOR(i,
0
,NL) {
FOR(j,
0
,NL) {
FOR(k,
0
,NL) {
m1.v[i][j]
+=
v[i][k]
*
m.v[k][j];
if
(m1.v[i][j]
>=
md) m1.v[i][j]
%=
md;
}
}
}
FOR(i,
0
,NL) {
FOR(j,
0
,NL) {
v[i][j]
=
m1.v[i][j];
}
}
}
};
int
main() {
int
k;
while
(scanf(
"
%d%d
"
,
&
k,
&
md)
!=
EOF) {
Matrix m0, m1;
int
i, j;
FOR(i,
0
,NL) {
//
printf("ok!");
scanf(
"
%d
"
,
&
m0.v[
0
][i]);
}
if
(k
<
10
) {
printf(
"
%d\n
"
, k);
continue
;
}
FOR(i,
1
,NL) {
m0.v[i][i
-
1
]
=
1
;
}
k
-=
10
;
m1
=
m0;
while
(k
>
0
) {
if
(k
&
1
) m0.Multiply(m1);
m1.Multiply(m1);
k
>>=
1
;
}
int
ans
=
0
;
FOR(i,
0
,NL) {
ans
+=
m0.v[
0
][i]
*
(NL
-
i
-
1
);
if
(ans
>=
md) ans
%=
md;
}
printf(
"
%d\n
"
, ans);
}
}
描述:求

分析:
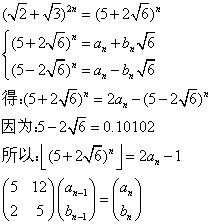
 代码
代码
#include
<
stdio.h
>
#include
<
string
.h
>
#define
NL 4
#define
MD 1024
#define
FOR(i,k,n) for(i=k;i<n;i++)
struct
Matrix {
int
v[NL][NL];
Matrix() {
memset(v,
0
,
sizeof
(v));
}
void
Multiply(Matrix m) {
int
i, j, k;
Matrix m1;
FOR(i,
0
,NL) {
FOR(j,
0
,NL) {
FOR(k,
0
,NL) {
m1.v[i][j]
+=
v[i][k]
*
m.v[k][j];
if
(m1.v[i][j]
>=
MD) m1.v[i][j]
%=
MD;
}
}
}
FOR(i,
0
,NL) {
FOR(j,
0
,NL) {
v[i][j]
=
m1.v[i][j];
}
}
}
};
int
main() {
int
t, n;
scanf(
"
%d
"
,
&
t);
while
(t
--
) {
scanf(
"
%d
"
,
&
n);
Matrix m0, m1;
m0.v[
0
][
0
]
=
5
;
m0.v[
0
][
1
]
=
12
;
m0.v[
1
][
0
]
=
2
;
m0.v[
1
][
1
]
=
5
;
m1
=
m0;
n
--
;
while
(n
>
0
) {
if
(n
&
1
) m0.Multiply(m1);
m1.Multiply(m1);
n
>>=
1
;
}
int
ans
=
m0.v[
0
][
0
];
ans
=
(ans
*
2
-
1
+
MD)
%
MD;
printf(
"
%d\n
"
, ans);
}
return
0
;
}
描述:Given a n × n matrix A and a positive integer k, find the sum S = A + A2 + A3 + … + Ak.
分析:
1. if k is odd then S = A + ... + Ak/2 + Ak/2+1(A + ... + Ak/2) ,else S = A + ... + Ak/2 + Ak/2(A + ... + Ak/2),
2. goto calculate k/2.
ps:用c++写的,效率很低,有待改进。
 代码
代码
#include
<
stdio.h
>
#include
<
string
.h
>
#define
NL 30
int
n, md;
class
Matrix {
public
:
int
v[NL][NL];
Matrix() {
memset(v,
0
,
sizeof
(v));
}
Matrix
&
operator
=
(
const
Matrix
&
m) {
for
(
int
i
=
0
; i
<
n; i
++
) {
for
(
int
j
=
0
; j
<
n; j
++
)
this
->
v[i][j]
=
m.v[i][j];
}
return
*
this
;
}
Matrix Multiply(Matrix m) {
Matrix m1;
for
(
int
i
=
0
; i
<
n; i
++
) {
for
(
int
j
=
0
; j
<
n; j
++
) {
for
(
int
k
=
0
; k
<
n; k
++
) {
m1.v[i][j]
+=
v[i][k]
*
m.v[k][j];
m1.v[i][j]
%=
md;
}
}
}
return
m1;
}
Matrix Add(Matrix m) {
Matrix m1;
for
(
int
i
=
0
; i
<
n; i
++
) {
for
(
int
j
=
0
; j
<
n; j
++
) {
m1.v[i][j]
=
(v[i][j]
+
m.v[i][j])
%
md;
}
}
return
m1;
}
Matrix Pow(
int
k) {
Matrix m1, m0;
m1
=
m0
=
*
this
;
k
--
;
while
(k
>
0
) {
if
(k
&
1
) m1
=
m1.Multiply(m0);
m0
=
m0.Multiply(m0);
k
>>=
1
;
}
return
m1;
}
void
Print() {
for
(
int
i
=
0
; i
<
n; i
++
) {
for
(
int
j
=
0
; j
<
n; j
++
)
printf(
"
%d
"
, v[i][j]);
printf(
"
\n
"
);
}
}
};
Matrix m0, m1;
Matrix cal(
int
k) {
Matrix m;
if
(k
==
1
)
return
m0;
if
(k
&
1
) {
Matrix mx
=
cal(k
/
2
);
Matrix my
=
m0.Pow(k
/
2
+
1
);
return
mx.Add(mx.Multiply(my).Add(my));
}
else
{
Matrix mx
=
cal(k
/
2
);
Matrix my
=
m0.Pow(k
/
2
);
return
mx.Add(my.Multiply(mx));
}
}
int
main() {
int
k;
scanf(
"
%d%d%d
"
,
&
n,
&
k,
&
md);
for
(
int
i
=
0
; i
<
n; i
++
) {
for
(
int
j
=
0
; j
<
n; j
++
)
scanf(
"
%d
"
,
&
m0.v[i][j]), m0.v[i][j]
%=
md;
}
m1
=
cal(k);
for
(
int
i
=
0
; i
<
n; i
++
) {
for
(
int
j
=
0
; j
<
n; j
++
) {
printf(
"
%d%c
"
, m1.v[i][j], (j
==
n
-
1
)
?
'
\n
'
:
'
'
);
}
}
return
0
;
}
