力扣刷题-数组-螺旋矩阵
模拟过程,但却十分考察对代码的掌控能力。
重点:循环不变量原则!
第一条原则:
模拟顺时针画矩阵的过程:
- 填充上行从左到右
- 填充右列从上到下
- 填充下行从右到左
- 填充左列从下到上
由外向内一圈一圈这么画下去。
第二条原则:
左闭右开原则!
这里一圈下来,我们要画每四条边,这四条边怎么画,每画一条边都要坚持一致的左闭右开,或者左开右闭的原则,这样这一圈才能按照统一的规则画下来。
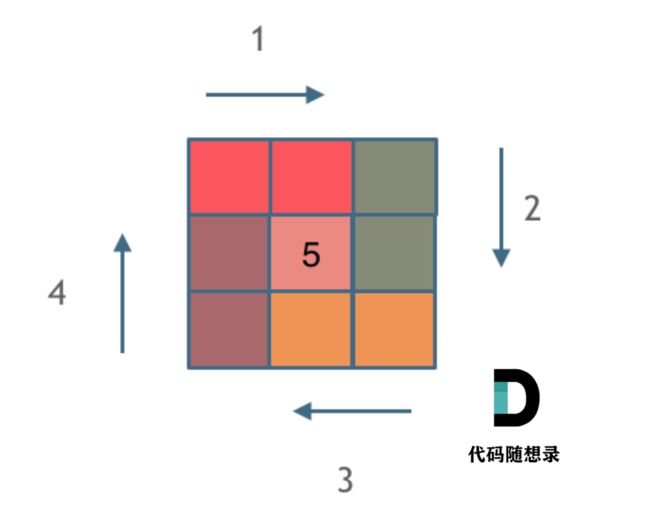
这里每一种颜色,代表一条边,我们遍历的长度,可以看出每一个拐角处的处理规则,拐角处让给新的一条边来继续画。这也是坚持了每条边左闭右开的原则。
59.螺旋矩阵II
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。
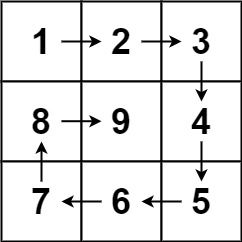
输入:n = 3
输出:[[1,2,3],[8,9,4],[7,6,5]]
class Solution(object):
def generateMatrix(self, n):
"""
:type n: int
:rtype: List[List[int]]
"""
# 螺旋矩阵 重点考察代码能力 不涉及算法
# 遇到判断循环边界的题目 要遵循 循环不变量 1. 上下行 左右列的遍历原则 2. 左闭右开原则
result = [[0]*n for _ in range(n)]
startx ,starty = 0, 0 # 起始位置 因为一般是循环里面用i j
loop = n // 2 # 循环个数 需要转几个圈
mid = n // 2 # 若n为奇数 需要单独处理中间的一个数 result[mid][mid]
offset = 1 # 第一圈offset当然为1 下一圈需要再加1 offset目的就是保持左闭右开原则
count = 1 # 计数 就是每个位置填充的数
# 开始循环
while loop > 0:
i = startx # 对于不同循环 每次起始的x y 不一样
j = starty
# 上行 左闭右开
for j in range(starty, n-offset):
result[startx][j] = count
count += 1
j += 1
# 右列
for i in range(startx, n-offset):
result[i][j] = count
count += 1
i += 1
# 下行
while j > starty:
result[i][j] = count
count += 1
j -= 1
# 左列
while i > startx:
result[i][j] = count
count += 1
i -= 1
loop -= 1 # 循环数减1
offset += 1 # offset加1
startx += 1
starty += 1
if n %2 :
result[mid][mid] = count
return result
54.螺旋矩阵
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
示例 1:(方阵)
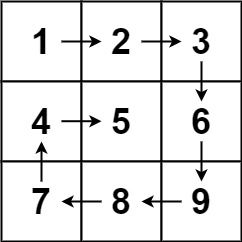
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
示例 2:
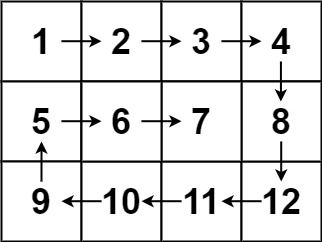
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
解题:
与59.螺旋矩阵II相同的是:两者都是模拟矩形的顺时针旋转,所以核心依然是依然是坚持循环不变量,按照左闭右开的原则
与59.螺旋矩阵II不同的是:前题中的螺旋矩阵是正方形,只有正方形的边长n一个边界条件,而本题中,需要考虑长方形的长和宽(m行和n列)两个边界条件。自然,m可以等于n,即前题可视为本题在m==n的特殊情况。
我们从最一般的情况开始考虑,与59.螺旋矩阵II题解对比起来,m和n的带入,主要引来两方面的差异:
- **loop的计算: **本题的loop计算与59.螺旋矩阵II算法略微差异,因为存在rows和columns两个维度,可自行分析,loop只能取min(rows, columns),例如rows = 5, columns = 7,那loop = 5 / 7 = 2
- mid的计算及填充: 1、同样的原理,本题的mid计算也存在上述差异; 2、 如果min(rows, columns)为偶数,则不需要在最后单独考虑矩阵最中间位置的赋值 如果min(rows, columns)为奇数,则矩阵最中间位置不只是[mid][mid],而是会留下来一个特殊的中间行或者中间列,具体是中间行还是中间列,要看rows和columns的大小,如果rows > columns,则是中间列,相反,则是中间行
可以自己举例画图分析。
class Solution(object):
def spiralOrder(self, matrix):
"""
:type matrix: List[List[int]]
:rtype: List[int]
"""
m = len(matrix) # 行数
n = len(matrix[0]) # 列数
result = []
if m == n: # 当矩阵为方阵时
startx, starty = 0, 0
offset = 1
loop = n // 2
mid = n // 2
while loop:
i = startx
j = starty
# 上行
for j in range(starty, n-offset):
result.append(matrix[startx][j])
j += 1
# 右列
for i in range(startx, n-offset):
result.append(matrix[i][j])
i += 1
# 下行
while j > starty:
result.append(matrix[i][j])
j -= 1
# 左列
while i > startx:
result.append(matrix[i][j])
loop -= 1
offset += 1
startx += 1
starty += 1
if n % 2:
result.append(matrix[mid][mid])
# m与n不等 则loop循环数量为 min(m,n) // 2 并且如果min(m,n)为奇数 则不再是中间位置 而可能是留下一行或者一列
if m != n:
startx, starty = 0, 0
offset = 1
loop = min(m ,n ) // 2
mid = min(m, n) // 2
while loop:
i = startx
j = starty
for j in range(starty, starty+n-offset): # 注意是startx+n-offset
result.append(matrix[startx][j])
j += 1
for i in range(startx, startx+m-offset):
result.append(matrix[i][j])
i += 1
while j > starty:
result.append(matrix[i][j])
j -= 1
while i > startx:
result.append(matrix[i][j])
i -= 1
loop -= 1
offset += 2 # 注意这里要加2 因为外圈遍历完后,再遍历内圈,内圈的矩阵行和列相比外圈都少了两个长度
startx += 1
starty += 1
# 处理额外的行/列数据
if min(m,n)%2:
if m>n: # 那就是额外的列
for i in range(mid, mid+m-n+1):
result.append(matrix[i][mid])
else:
for j in range(mid, mid+n-m+1):
result.append(matrix[mid][j])
return result
其实可以不用分:
class Solution(object):
def spiralOrder(self, matrix):
"""
:type matrix: List[List[int]]
:rtype: List[int]
"""
m = len(matrix) # 行数
n = len(matrix[0]) # 列数
result = []
# if m == n: # 当矩阵为方阵时
# startx, starty = 0, 0
# offset = 1
# loop = n // 2
# mid = n // 2
# while loop:
# i = startx
# j = starty
# # 上行
# for j in range(starty, n-offset):
# result.append(matrix[startx][j])
# j += 1
# # 右列
# for i in range(startx, n-offset):
# result.append(matrix[i][j])
# i += 1
# # 下行
# while j > starty:
# result.append(matrix[i][j])
# j -= 1
# # 左列
# while i > startx:
# result.append(matrix[i][j])
# loop -= 1
# offset += 1
# startx += 1
# starty += 1
# if n % 2:
# result.append(matrix[mid][mid])
# m与n不等 则loop循环数量为 min(m,n) // 2 并且如果min(m,n)为奇数 则不再是中间位置 而可能是留下一行或者一列
startx, starty = 0, 0
offset = 1
loop = min(m ,n ) // 2
mid = min(m, n) // 2
while loop:
i = startx
j = starty
for j in range(starty, starty+n-offset): # 注意是startx+n-offset
result.append(matrix[startx][j])
j += 1
for i in range(startx, startx+m-offset):
result.append(matrix[i][j])
i += 1
while j > starty:
result.append(matrix[i][j])
j -= 1
while i > startx:
result.append(matrix[i][j])
i-=1
loop -= 1
offset += 2 # 注意这里要加2 因为外圈遍历完后,再遍历内圈,内圈的矩阵行和列相比外圈都少了两个长度
startx += 1
starty += 1
# 处理额外的行/列数据
if min(m,n)%2:
if m>n: # 那就是额外的列
for i in range(mid, mid+m-n+1): # 注意是mid
result.append(matrix[i][mid])
else: # 那就是额外的行
for j in range(mid, mid+n-m+1):
result.append(matrix[mid][j])
return result
重点在于考虑到m!=n时候如何判断循环圈数,以及什么时候要考虑循环完毕之后剩余的元素,以及如何处理。
参考:https://programmercarl.com/