Matlabe绘图plot求单调区间极大极小最值问题
文章目录
- Matlabe绘图单调区间极大值
-
- 求函数极值
- 求单调区间
- 求某区间最值问题
- format函数的调用格式
Matlabe绘图单调区间极大值
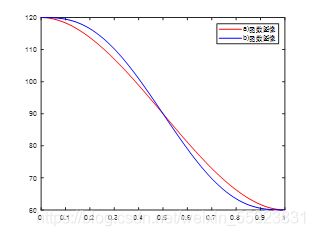
t=[0:0.01:1];
q1=120-180*t.^2+120*t.^3;
q2=120-600*t.^3+900*t.^4-360*t.^5;
plot(t,q1,'r'); hold on; %范围 函数 颜色
plot(t,q2,'b');
legend('a)函数图像','b)函数图像') %要按函数的顺序来添加
x = 0:0.5:4*pi
y1 = sin(x)
y2 = cos(x)
y3 = 1./(1+exp(-x))
y4 = (1/(2*pi)^0.5).*exp(((-1).*(x-2*pi).^2)./(2*2^2))
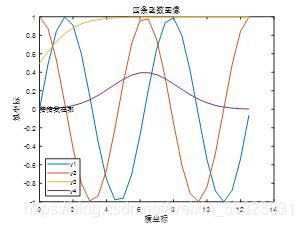
plot(x,y1,x,y2,x,y3,x,y4)
//加上简单图形标注
title('四条函数图像')
xlabel('横坐标')
ylabel('纵坐标')
text(0,0,'猜猜我在哪')
legend('y1','y2','y3','y4','Location','southwest')
x=[-5:0.01:5];
y=2*x.*sin(x);
a=plot(x,y) %绘制函数并获得其句柄
hold on %保持图像
grid on %增加网格
xlabel('x'); %x轴
ylabel('y'); %y轴
title('y=2xsin(x)'); %标题
legend('y=2xsin(x)'); %图例
a.Color='r'; %曲线颜色设置
x=[-5:0.01:5];
y=@(x) 2*x.*sin(x);
fplot(y)
hold on %保持图像
grid on %增加网格
xlabel('x'); %x轴
ylabel('y'); %y轴
title('y=2xsin(x)'); %标题
legend('y=2xsin(x)'); %图例
a.Color='r'; %曲线颜色设置
求函数极值
求函数极小值命令格式:[x,minf]=fminbnd(‘f’,a,b)
求函数极大值命令格式:[x, maxf]=fminbnd(-f,a,b),maxf-maxf
①函数 fminbnd(f,a,b)是对f(x)在(a,b)上搜索极小值点,若求f(x)的极大值点,需对-f(x取极小值点,所得即为f(x)的极大值点。
②当不知道极值点所在的范围(a,b)时,可先用绘图函数绘出函数曲线图形,大致确定极值点所在的范围,再用求极值点的函数求得极值点。
例1:求fx3-x2-x+1在(-2.2)内的极小值与极大值。
程序如下:
syms x
[x1, minf]=fminbnd('x^3-x^2-x+1’,-2, 2).
[x2,maxf ]-fminbnd('-x^3+x2+x-1',-2, 2)
maxf=-maxf.
运行结果:x1=1.0000
minf=3.5776e-010
x2=-0.3333
maxf=-1.1852
maxf=1.1852
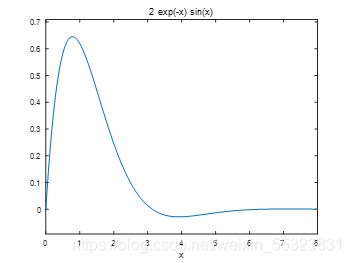
例2:求f=2e-sinx的极大值与极小值
因不知道初始点的位置,故首先画出曲线图确定搜索的初始点
程序如下:
symsX
ezplot(2exp(-x)*sin(x),[0,8])
%画出函数图观察极值点观察到:极大值点约在[0,2],极小值点约在[2,5]
[x1, minf ]=fminbnd( ‘2*exp (-x)*sin(x)’, 2, 5)
[x2, maxf ]=fminbnd(‘-2*exp (-x)*sin (x)’, 0, 2)
maxf=-maxf.
minf=-0.0279
x2=0.7854
maxf=-0.6448
maxf=0.6448
求单调区间
syms x
f=3*x-x.^3;
diff(3*x-x.^3) %求一阶导数判断正负
zhudian =solve(diff(f,x)) %跟据驻点写出区间
求某区间最值问题
输入:help+函数名(查询用法)
- fminban
- fmincon
- fminsearch
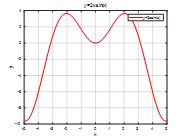
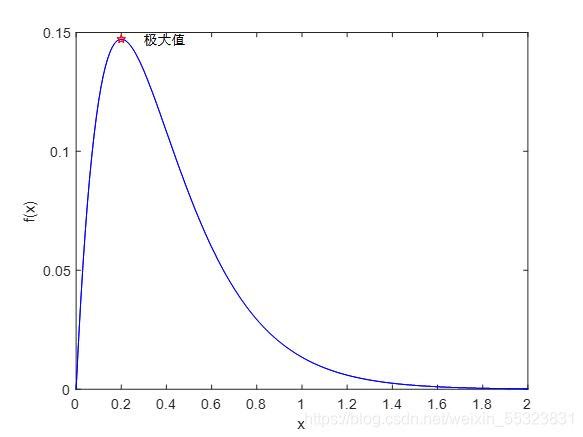
例:求 matlab图像的极大值,可以用 fminsearch()极小值函数来求解。用 fminsearch()求极大值问题,应将表达式改为反函数形式。例:求f(x)=2xexp(-5x)在原点附近的极大值,并作图标注极大值位置。
解:问题等价于-f(x)的极小值
x=0:0.01:2
y=2*x.*exp(-5*x)
plot(x,y,’b-‘)
hold on
[x1,f1]=fminsearch(@(x)-(2*x.*exp(-5*x)),0)
plot(x1,-f1,’rp’;)
text(x1+0.1,-f1’极大值’)
xlabel(‘x’),ylabel(‘f(x)’)
format函数的调用格式
1.format short:默认格式,小数点后保留4位

2.format long:有效数字16位

3.format long e:有效数字16位加3位指数
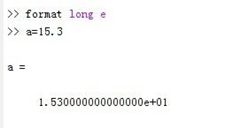
4.format short e:有效数字5位加3位指数

5.format bank:保留两位小数位

6.format +:只给出正负

7.format rational:以分数的形式表示
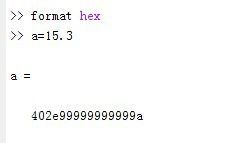
8.format hex:以16进制数表示

9.format long g:15位有效数

10.format short g:5位有效数