一文弄懂基于图搜索的路径规划算法A*与Dijkstra（有python代码）

基于图搜索路径规划-Dijkstra与A*
关注晓理紫并回复Dijkstra，A*获取代码
[晓理紫]

1、 基于图搜索路径规划算法的框架

基于图搜索的路径规划的算法框架都很统一，下面便是通用的算法框架

1、维护一个容器以存储要访问的所有节点 OpenList
2、容器以启动状态起点 $X_s$ 进行初始化 OpenList.push($X_s$)
3、循环 （OpenList 为空或者找到目标点退出循环）
    4、根据一些预定义的评分函数从容器中删除节点（根据一定的规则对OpenList进行排序）（注意：Dijkstra与A*在此处有所不同）
        访问节点（可能添加到ClosedList中）
    5、扩展：获取该节点的所有邻居（找到该节点的邻居节点）（JPS与A*在此处有所不同）
        发现所有邻居
    6、将邻居推入容器 OpenList.push($X_n$)（符合条件的）
7、结束循环

1.1 一些问题

• 什么时候结束循环？

  • 当 OpenList 为空或者找到目标点退出循环

• 如何处理图是循环的？

  • 把从 OpenList 删除的节点存储在 ClosedList 中并标记为已访问，下次不在访问

2、广度优先搜索与深度优先搜索

2.1 广度优先搜索

广度搜索采用的是队列进行存储节点，先进先出

2.2.1 搜索过程

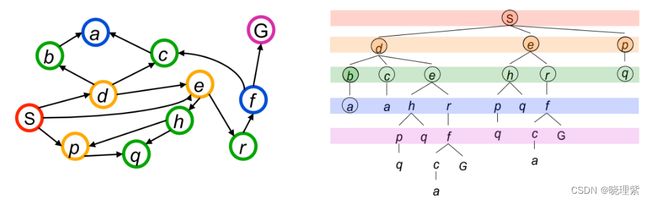
1、openList使用开始节点初始化: [s]
2、弹出首位元素s并获取s的邻居，把邻居加入到openList：[d,e,p] 把s加入closedList：[s]
3、弹出首位元素d并获取d的邻居，把邻居加入到openList：[e,p,b,c,e],把d加入closedList：[s,d]
4、弹出首位元素e并获取e的邻居，把邻居加入到openList：[p，b,c,e,h,r],把e加入closedList：[s,d,e]
5、弹出首位元素p并获取p的邻居，把邻居加入到openList：[b,c,e,h,r,q],把p加入closedList：[s,d,e,p]
6、弹出首位元素b并获取b的邻居，把邻居加入到openList：[c,e,h,r,q,a],把b加入closedList：[s,d,e,p,b]
7、弹出首位元素c并获取c的邻居，把邻居加入到openList：[e,h,r,q,a,h,r],把c加入closedList：[s,d,e,p,b,c]
8、弹出首位元素e,e已经访问就不在访问：[h,r,q,a,h,r]，[s,d,e,p,b,c]
...
依次类推直到openList为空或者找到目标为止

2.3 深度优先搜索

深度优先搜索采用的是栈进行存储节点，先进后出

2.3.1 搜索过程

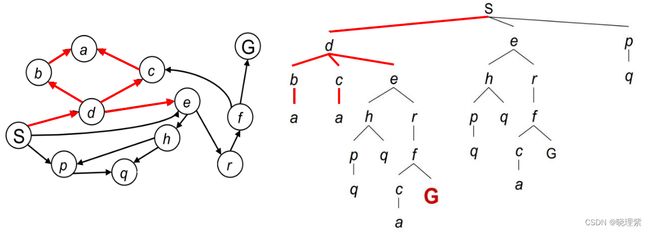
1、openList使用开始节点初始化: [s]
2、弹出首位元素s并获取s的邻居，把邻居加入到openList：[p,e,d] 把s加入closedList：[s]
3、弹出首位元素d并获取d的邻居，把邻居加入到openList：[p,e,e,c,b],把d加入closedList：[s,d]
4、弹出首位元素b并获取b的邻居，把邻居加入到openList：[p,e,e,c,a],把b加入closedList：[s,d,b]
5、弹出首位元素a并获取a的邻居，把邻居加入到openList：[p,e,e,c],把a加入closedList：[s,d,b,a]
6、弹出首位元素c并获取c的邻居，把邻居加入到openList：[p,e,e,a],把c加入closedList：[s,d,b,a,c]
7、弹出首位元素a,a已访问不再处理[p,e,e]，[s,d,b,a,c]
8、弹出首位元素e,并获取e的邻居，把邻居加入到openList：[p,e,h,r],把e加入closedList：[s,d,b,a,c,e]
...
依次类推直到openList为空或者找到目标为止

3、贪心算法

BFS 和 DFS 根据“最先进入”或“最后进入”来选择边界外的下一个节点。贪婪最佳优先根据某种规则（称为启发式）选择“最佳”节点。所谓的启发就是对从当前点到目标点距离的猜想。

3.1、启发函数设计的原理

• 启发式方法可以引导更快的走向目标。
• 启发式应该易于计算。

3.2、广度搜索与贪心搜索的对比

广度	贪心

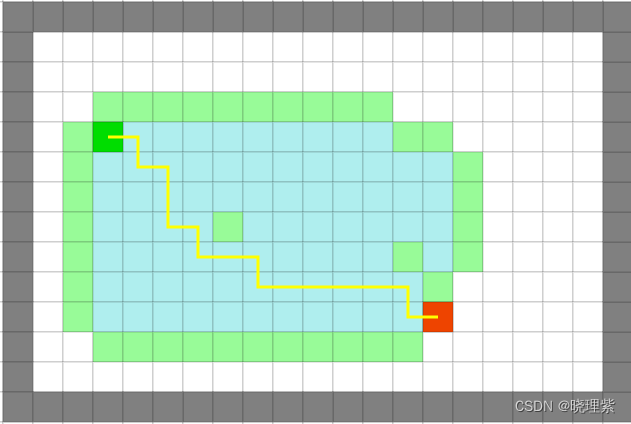
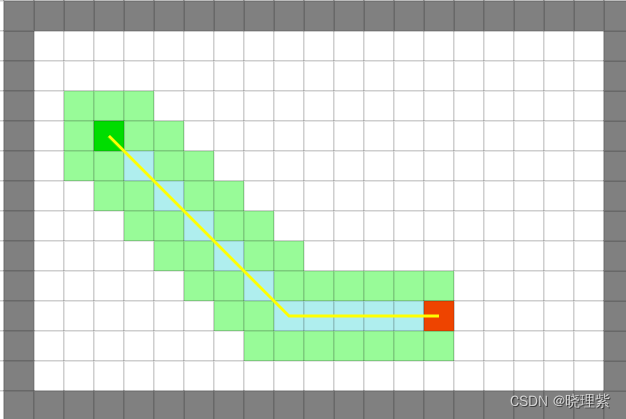
可以看出贪心算法的速度之快。但是贪心出来的路径一定是最优的么？

4、Dijkstra 算法

Dijkstra 的策略是扩展/访问累积成本 g(n)最便宜的节点，也就是当节点插入到 OpenList 中时通过 g(n)的值进行排序，值越小就越先弹出，其中

• g(n)：从起始状态到节点“n”的累积成本的当前最佳估计(从开始节点到当前节点需要的最小代价)

• 更新节点“n”的所有未扩展邻居“m”的累积成本 g(m)

• 保证已扩展/访问的节点从开始状态起具有最小的成本

4.1、代码框架

1、维护一个优先级队列，存放所有需要扩容的节点 (优先队列通过g(n)对插入节点进行排序，确保最小g(n)可以优先弹出)
2、优先级队列初始化为起始状态  $X_s$
3、为图中的所有其他节点分配 g($X_s$ )=0 和 g(n)=无穷大（n是未访问节点）
4、循环（直到队列为空或者找到目标节点）
    如果队列为空，则返回FALSE； 退出;
    从优先级队列中删除 g(n) 最低的节点“n”
    将节点“n”标记为已展开（加入closedList）
    对于节点“n”的所有未扩展邻居“m”进行扩展
      如果 g(m) = 无穷大（说明未访问过）
        g(m)= g(n) + Cnm（从起点到n节点的代价g(n)+从n节点到m节点的代价）
        将节点“m”推入队列（加入openList）
      如果 g(m) > g(n) + Cnm（说明已经访问过，之修改g值不加入openList中）
        g(m)= g(n) + Cnm
5、结束循环

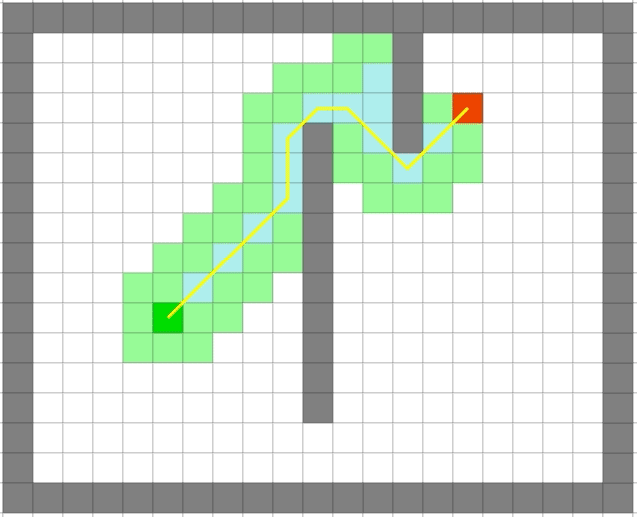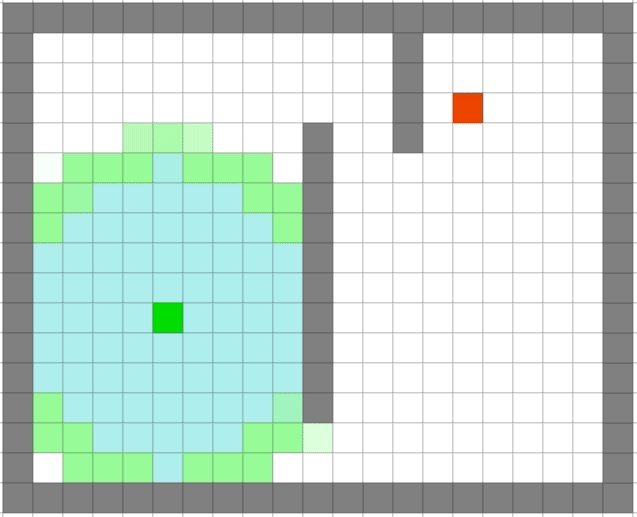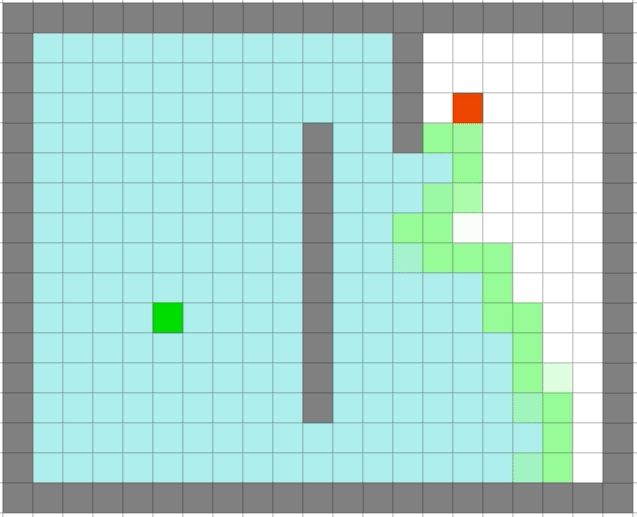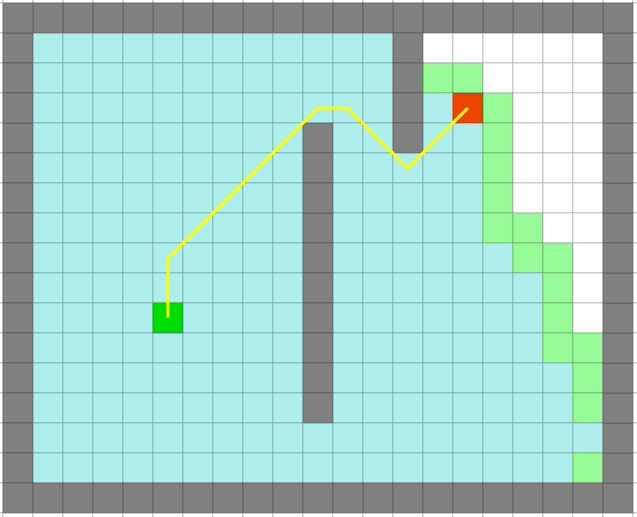
4.2、 搜索过程

每次都考虑访问从起点到当前点 n 最小代价的的节点 n

1、openList使用开始节点初始化: [s:0] (节点s的g为0)
2、弹出首位元素s并获取s的邻居，把邻居加入到openList并排序：[p:1,d:3,e:9] 把s加入closedList：[s]
3、弹出首位元素p并获取p的邻居，把邻居加入到openList并排序：[d:3,e:9,q:17],把p加入closedList：[s,p]
4、弹出首位元素d并获取d的邻居，把邻居加入到openList并排序：[b:7,e:8,c:14,q:17](通过d节点到e的代码变小了由9变成了8),把d加入closedList：[s,p,d]
...
依次类推直到openList为空或者找到目标为止

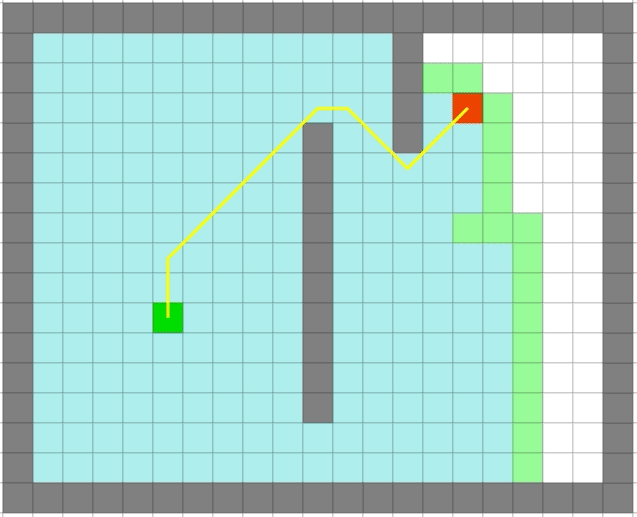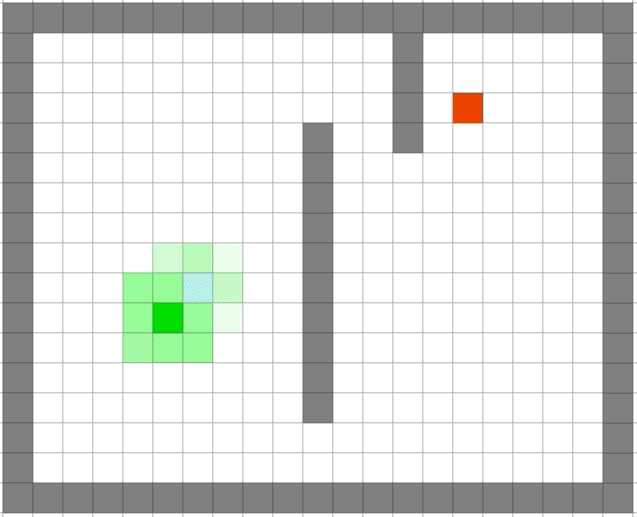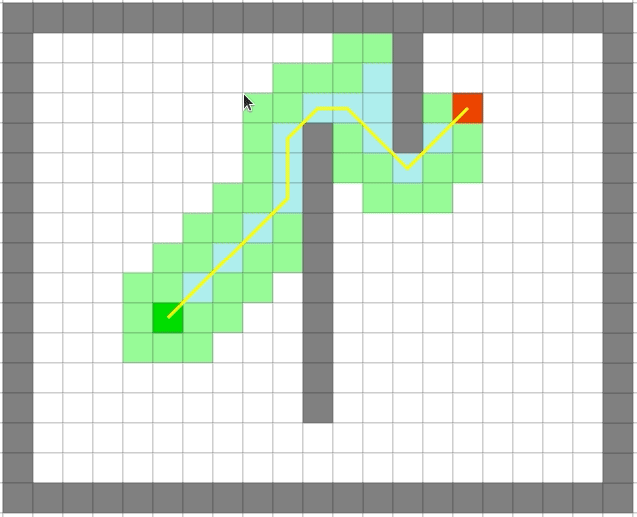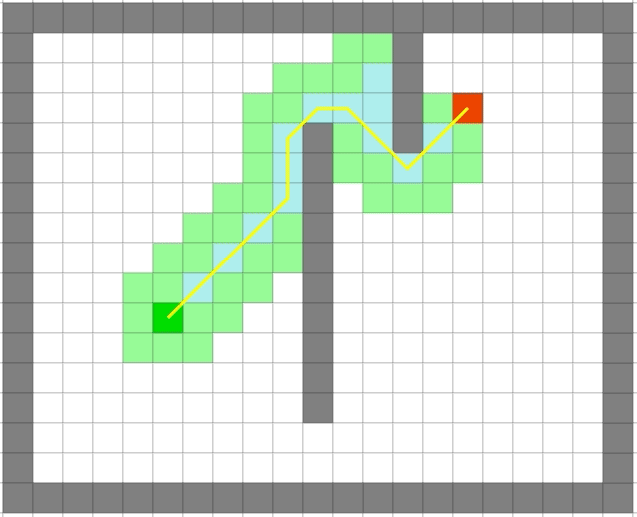
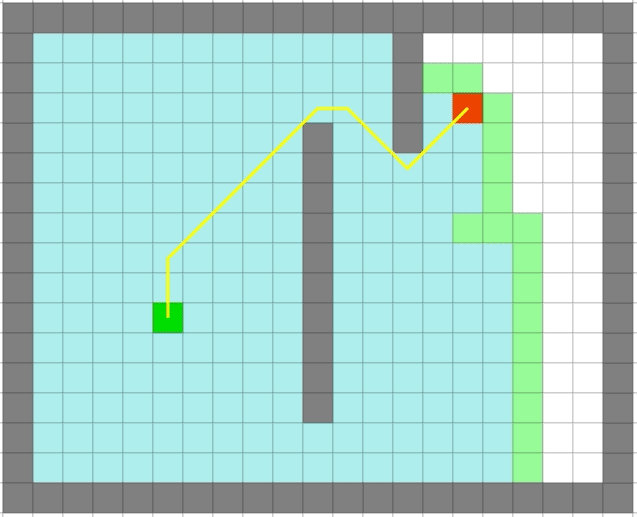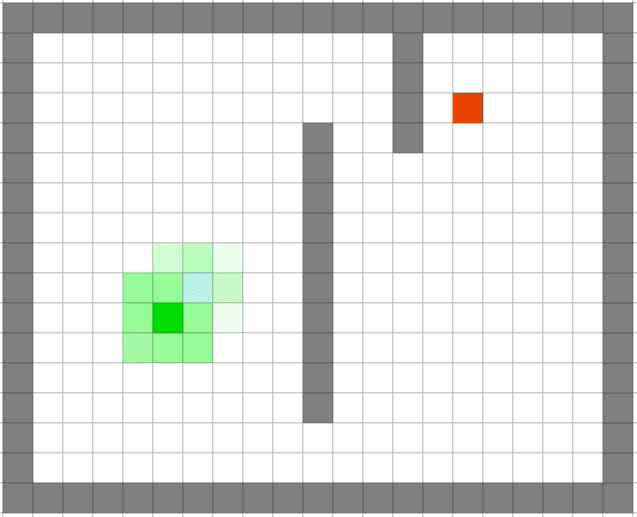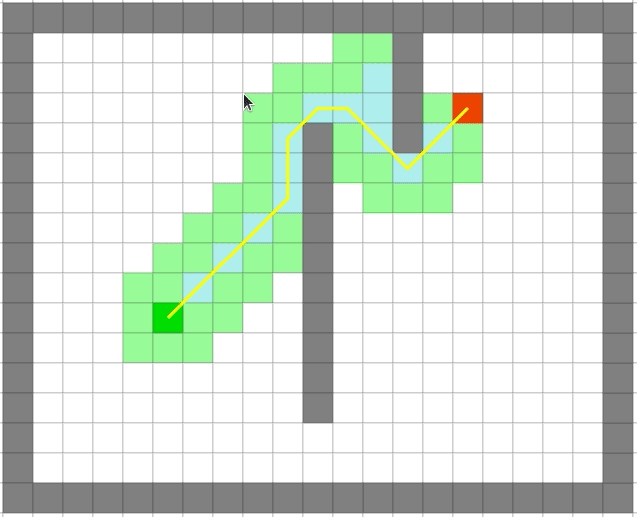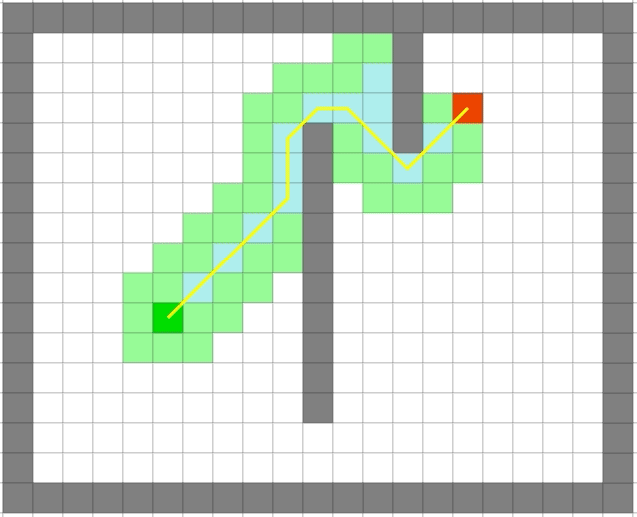
4.3、 演示

Dijkstra	贪心

贪心算法依旧很快，但是它是最优的么：

Dijkstra	贪心

可以看出贪心算法虽然很快但是在一些场景并不能得到最优解。

5、A* 算法

Dijkstra 算法可以到的最优解但是搜索速度慢，贪心算法速度快但是无法得到最优解，那么有没有既可以得到最优解速度又快的算法呢。答案是有的。

A* 算法 = Dijkstra 算法 + 贪心算法（因为 A*算法排序依据 f = g + h）

5.1、名词说明

• 累计成本(g(n)):从起始状态到节点“n”的累积成本的最小代价

• 启发式(h(n)):从节点 n 到目标状态的估计最小成本（即目标成本）

• 最小总成本(f(n) = g(n) + h(n))从起始状态到目标状态经过节点“n”的最小估计成本

• Openlist 排序策略：扩展最便宜的节点 f(n) = g(n) + h(n)

• 更新节点“n”的所有未扩展邻居“m”的累积成本 g(m),保证已扩展的节点从起始状态开始具有最小的成本

5.2、代码框架

1、维护一个优先级队列，存放所有需要扩容的节点（OpenList）
2、所有节点的启发式函数 h(n) 都是预先定义的（可采用曼哈顿距离， 欧氏距离等）
3、优先级队列初始化为起始状态 $X_s$(OpenList.push($X_s$))
4、为图中的所有其他节点分配 g($X_s$)=0 和 g(n)=无穷大
5、循环（直到队列为空或者找到目标节点））
    如果队列为空，则返回FALSE； 返回;’
    从优先级队列中删除 f(n)=g(n)+h(n) #最低的节点“n”（h(0)==0时是Dijkstra算法，g(n)==0时是贪心算法）
    将节点“n”标记为已展开  #将n加入ClosedList中
    对于节点“n”的所有未扩展邻居“m”
      如果 g(m) = 无穷大  #说明未扩展
        g(m)= g(n) + Cnm  #（从起点到n节点的代价g(n)+从n节点到m节点的代价）
        将节点“m”推入队列  #OpenList.push(m)
      如果 g(m) > g(n) + Cnm
        g(m)= g(n) + Cnm   #说明已经访问过，只修改g值不加入openList中

6、结束循环

5.3、搜索过程

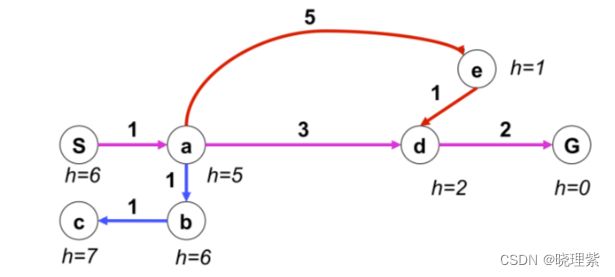
1、openList使用开始节点初始化: [s:6] (节点s的f为6)
2、弹出首位元素s并获取s的邻居，把邻居加入到openList并排序：[a:6](g=1,h=5) 把s加入closedList：[s]
3、弹出首位元素a并获取a的邻居，把邻居加入到openList并排序：[d:6,e:7,b:12]把a加入closedList：[s,a]
4、弹出首位元素d并获取d的邻居，把邻居加入到openList并排序：[g:6,e:7,b:12]把d加入closedList：[s,a,d]
5、弹出首位元素g，到达目标退出

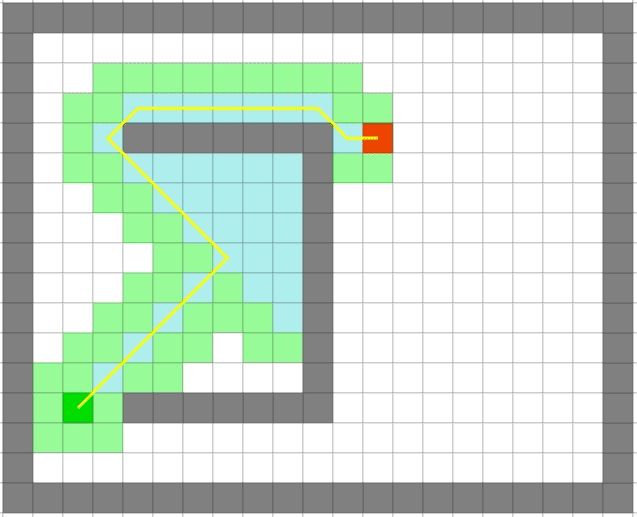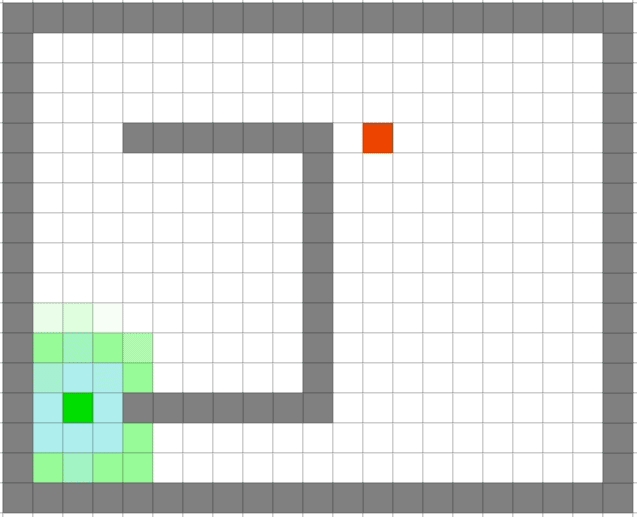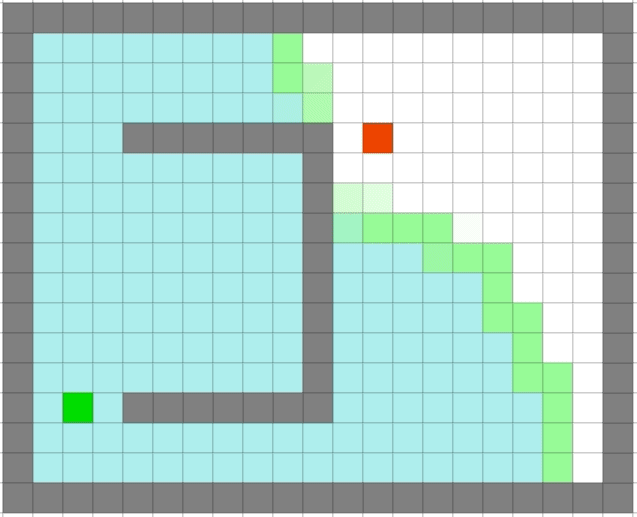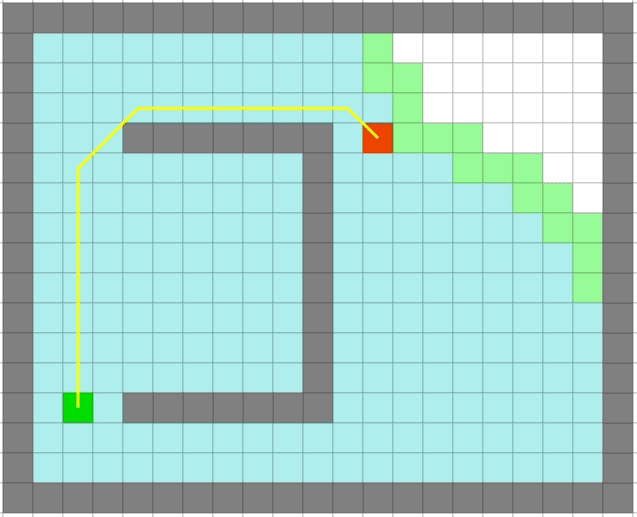
5.4、问题

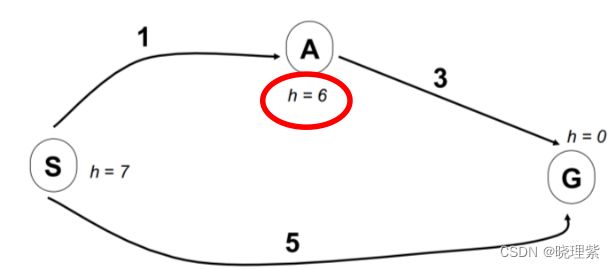
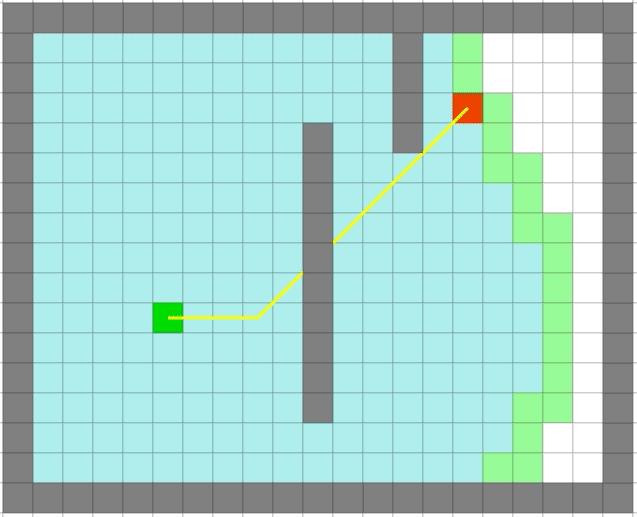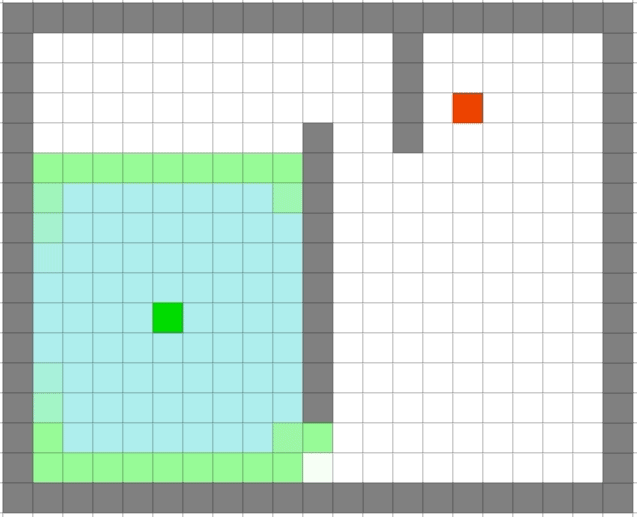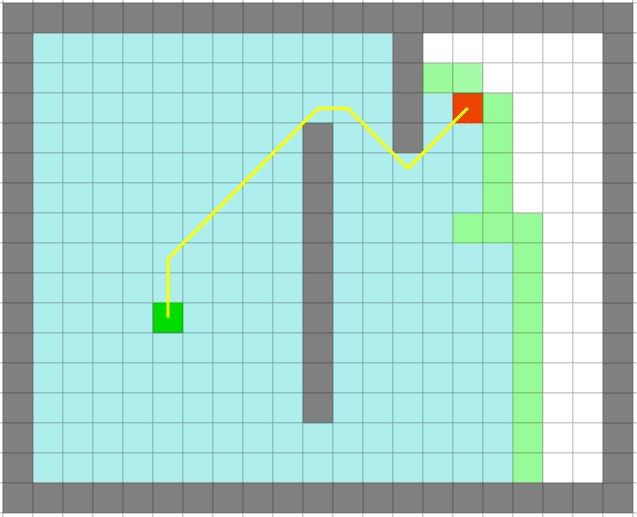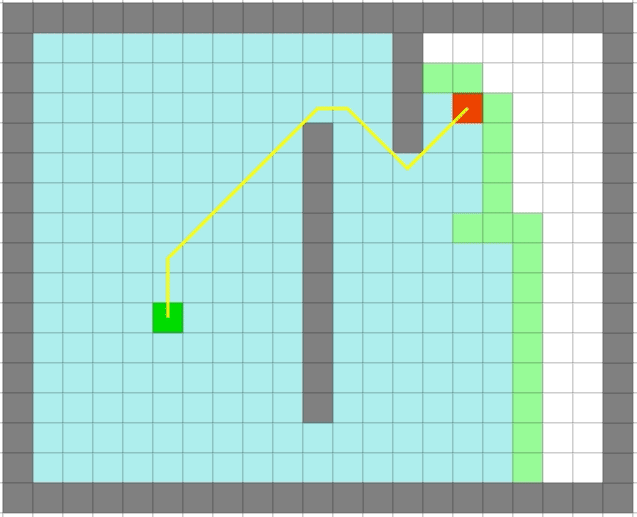
A*找到的路径一定是最优的么

• 从图中可以看出来，按照 A*算法直接走 S->G，其实 S->A->G 才是最优路径。

• 问题原因是 A 点到目标点估计的代价 h 大于了真是的代价。为了解决此问题，需要估计值 h 小于等于到目标的真实代价。

5.5、启发函数的选择

选择原则：对于所有节点“n”，h(n) <= h*(n)，其中 h*(n) 是从节点“n”到达目标的真正最低代价

• 哪些启发函数是可接受的呢

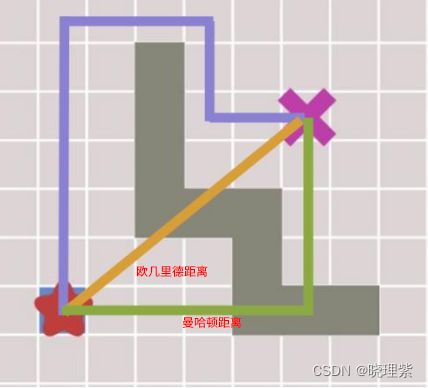
• 欧几里德距离:欧几里德距离（L2 范数）是可接受的，无论小车是否可对角行走估计出来的值总是小于等于实际值
• 曼哈顿距离 曼哈顿距离（L1 范数）分情况可接受，当小车不允许对角线行走时是可接受的，当小车允许对角线行走时是不可接受的。因为猜测代价 2>真实代价根号 2
• L∞ 范数距离是可接受的，（L∞ 范数距=max(|x2-x1|,|y2-y1|)）
• 0 距离总是可接受的，当 h=0 时一定是小于真实代价的

5.6、Dijkstra’s VS A*

A*	Dijkstra
)

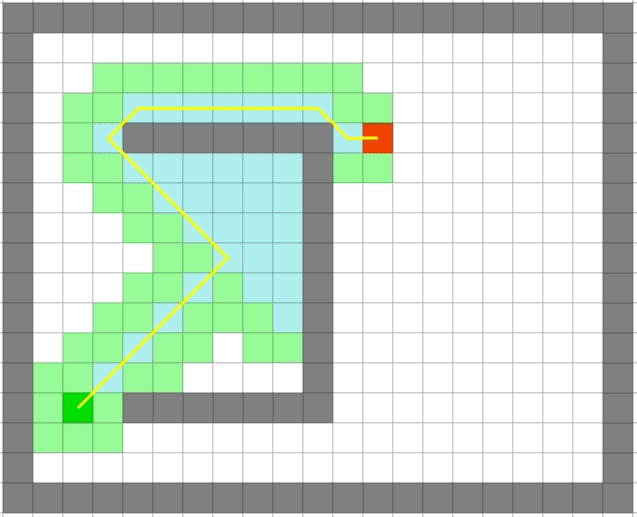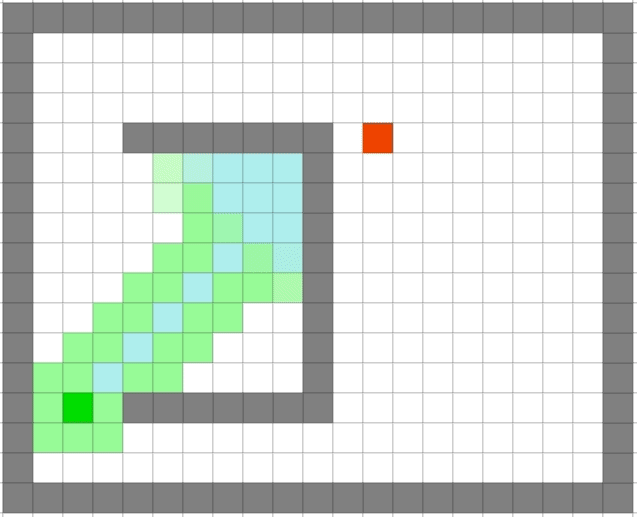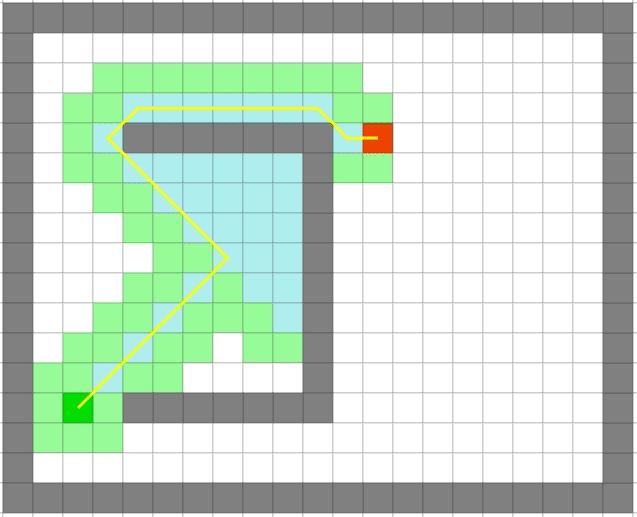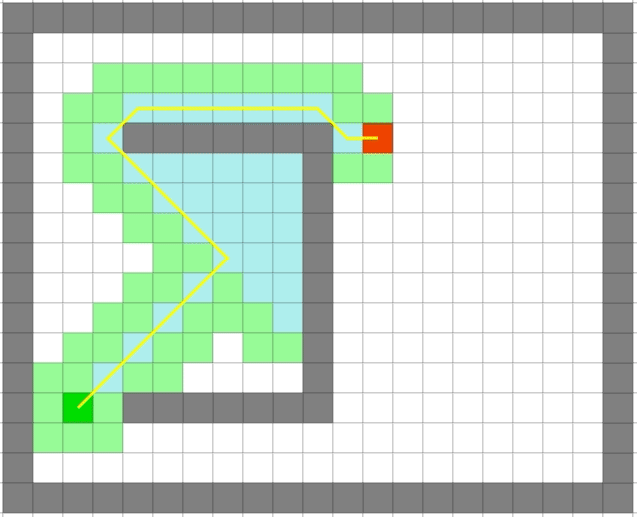
可以看出 A*可以高效的进行搜索并且可以得到比较好的路径

5.7、次优解

有时为了达到更快的速度，A*可以向贪心方向发展放弃最优解的到次优速度很快的解。

只要把启发函数的比值提高就行，基于 f = ag + εh 扩展状态，ε > 1 = 偏向更接近目标的状态。这就是权重 A*

A*(ε ==1)	A*(ε ==2)

5.8 使用经验

• 如何将网格表示为图形？

  • 每个单元格都是一个节点。 用边连接相邻的单元格。

• 如何选择最好的启发式函数

  • 通常使用欧式距离，L∞ 范数距离是较好的但是不最好的，因为没有一个是紧的，搜索范围都是较宽的。
    

主要原因是在搜索过程中存在需要 f 值相同的对称路径，只要让 f 值略有差别就可以很好的解决这个问题。

解决方法：

• 选择最好的启发函数:对角启发函数 （Diagonal Heuristic）

  • 2D 计算公式：dx=abs(node.x −goal.x)，dy=abs(node.y −goal.y)，h=(dx+dy)+(√2−2)∗min(dx,dy)

• 打破对称性

  • 通过稍微干扰 ℎ，操纵 值打破平局，使相同的 值不同。

    h = hx(1.0+p)

    p < / ℎ （一步的最小成本/预期最大路径成本）

  • 首选从起点到目标沿直线的路径。

    1 = （ . − . ）

    1 = (. − . )

    2 = . − .

    2 = . − .

    = (1 × 2 − 2 × 1)

    h = ℎ + × 0.001

• 使用 Jump Point Search (JPS)算法
  下面节继续介绍JPS算法

6 代码获取方式

搜索并关注晓理紫并回复有AD获取代码

{晓理紫|小李子}喜分享，也很需要你的支持，喜欢留下痕迹哦！