【深度学习概述学习小结】
深度学习概述学习小结
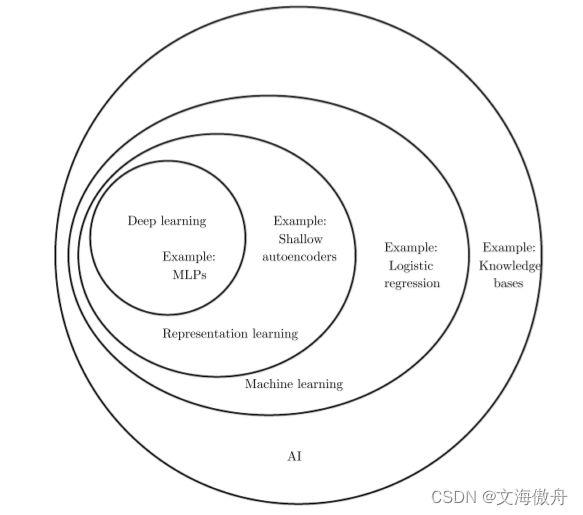
- 人工智能、机器学习与深度学习关系
- 深度学习
-
- 深度学习历史
- 深度学习基础知识
-
- 神经元
- 参数更新与误差反向传播
- Pytorch代码学习
-
- 螺旋分类整体思考
- 实验对比
- 继续实验
人工智能、机器学习与深度学习关系
在人工智能领域,对于人们而言十分复杂而庞大的问题对机器来说也许并不难,因为这些问题可以通过一系列正式的数学表达式来描述,真正困难的问题是那些对于人类来说十分直觉、也许我们将其视为本能的一些问题,例如目标检测、语音识别等。
对于可以通过一系列规则来描述的问题,其并不要求机器对这个世界要求什么过多知识。例如1997年IBM的深蓝(Deep Blue),象棋规则可以通过简洁的规则描述,从而由机器轻松攻破。
而对于那些“直觉性”的问题,学界有两种思路,其中一种是通过将世界中的知识通过一种正式语言来描述从而让机器去理解,让机器通过这些规则自动去做逻辑推理,但基于这种思路的项目都没有取得成功。另一种思路是让机器从经验中去学习,通过提供原始数据让机器去从中自己挖掘,我们可以避免人为为机器去收集所需的知识。基于这种想法的方法称为机器学习。
由上可知,这种机器学习的效果依赖于所给予的数据的表达。通常情况下,我们并不是给予一个原始的对象,而是关于该对象的若干数据,我们称之为特征(feature),机器学习通过学习特征与结果(target)之间的关系去解决问题,一些简单的机器学习算法,例如逻辑回归等都是这种思路。
但对于很多任务来说,我们并不知道应该提供哪些特征数据给机器去学习,或者在众多数据中选择哪些作为特征。对于这类问题其中一中解决方法是,我们不再寻求从特征表达到结果目标的映射(mapping),而是去学习表达本身。我们不再人为去挑选数据,而是让机器去寻找一系列好的特征去作为数据。这其中一个好的例子便是自动编码机(autoencoder)。其包含两个部分,encoder部分将原始输入数据转化成不同的表达,而decoder部分再将新的表达还原成原形式。我们希望所学到的特征不仅是通过直接可以量化的一些指标,而且希望其可以包含一些没有被观察到但可以影响到最终结果的特征,这些特征也许是在人的大脑中重新构造出以提供对原始数据更为简洁的解释的量,例如人的口音,这种特征几乎完全得靠人来判断,显然对于这类高度抽象的特征机器是十分难去直接从原始数据中抽离。对于这种问题,深度学习可以通过将复杂的特征表达分解为更为简单的表达,例下图所示:
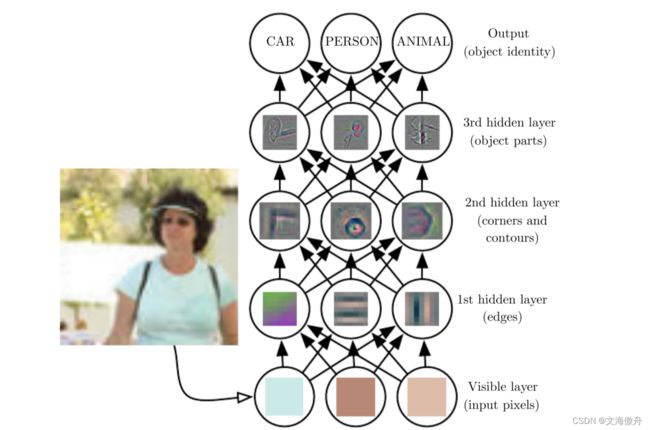
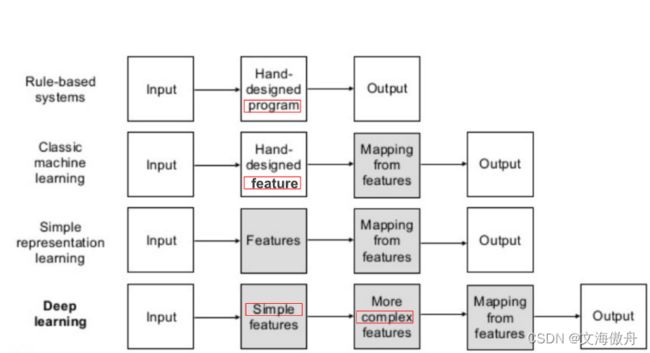
上图表示了不同方法对于特征提取的差异。
深度学习
深度学习历史
康奈尔大学Frank Rosenblatt于1957年提出感知器(Perceptron),其是第一个具有自组织学习能力的数学模型,但其存在一定局限,主要表现在下面两个问题:
- 单层的神经网络无法解决不可线性划分的问题,典型例子如异或门
- 当时的电脑完全没有能力完成神经网络模型所需要的超大计算量
至此,人工智能研究进入第一个低潮。在这时,感知器使用所谓“梯度下降”算法纠错,耗费的计算量和神经元数目的平方成正比,这需要巨大的计算硬件。在1986年,Hinton和David Rumelhart提出BP算法,使纠错的运算量下降到和神经元数目本身成正比,并通过增加隐层(hidden layer)解决了异或问题,于是神经网络研究开始复苏,例如Yann Lecun使用反向传播算法在手写邮政编码上取得巨大成功,但与此同时传统机器学习领域也在发展,支持向量机算法具有完整的理论基础,同时BP算法也出现了梯度消失等问题,于是神经网络研究逐渐被向量机替代,深度学习陷入了第二次低潮。
在ILSVRC2012中,由Hinton和两个研究生利用CNN+Dropout+RELU最终在比赛中以错误率15.3%夺得第一,这时神经网络二十多年来第一次在图像识别领域大幅度击败其他技术,于是神经网络迎来复兴。之后神经网络发展飞速,如下图所示.
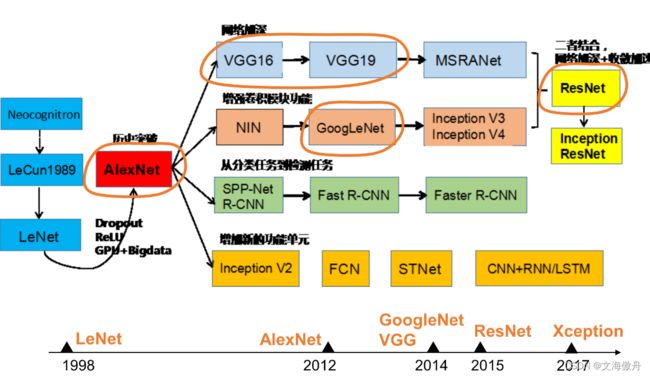
深度学习基础知识
神经元
神经元由人脑神经细胞抽象而来,对于输入数据进行线性转化,可以抽象表示为:
y = ∑ i = 0 n w i ∗ x + b i . \ y= \sum_{i=0}^n \ w_i * \ x + \ b_i. y=i=0∑n wi∗ x+ bi.
可以看到这里仅进行了线性变化,对于数据中的特征提取有限,故引入非线性变换函数–激活函数
常用激活函数有ReLU函数,其图像为
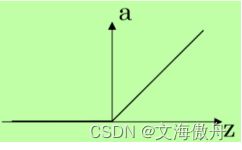
参数更新与误差反向传播
误差反向传播是更新网络参数的一种方法。
对于常见的一个网络其通常可以表示为:
g ( x ) : = f L ( W L f L − 1 ( W L − 1 . . . f 1 ( W 1 x ) . . . ) ) \ g(x) := \ f^L(W^L f^{L-1} (W^{L-1} ... f^1(W^1x)...)) g(x):= fL(WLfL−1(WL−1...f1(W1x)...))
其中x表示为输入的向量,L是层数, W L = ( w j k l ) W^L=(w_{jk}^{l}) WL=(wjkl)表示第L-1到第L层的权重参数,其中 w j k l w_{jk}^{l} wjkl表示第l-1层的第k个节点和第l层第j个节点的权重参数, f L f^L fL表示第L层的激活函数
我们希望最终我们的网络可以预测准确率高,其可以表示为网络输出的分类结果与实际真实结果相同,转化为数学表达式为
C ( y i , g ( x i ) ) C(y_i,g(x_i)) C(yi,g(xi))
这里C为损失函数,对于每一个输入-输出对{ x i , y i x_i,y_i xi,yi}我们都通过损失函数来计算,我们最终希望计算损失函数最小值,即通过计算损失函数的微分为0来获得,这里便得到
∂ C / ∂ w j k l \partial C/ \partial w_{jk}^{l} ∂C/∂wjkl
注意这里损失函数是一个嵌套函数,故在微分过程中会涉及链式法则,这样由链式法则可以知道最终整个微分值只有首先计算出最外部的函数积分,再计算次外部的函数依次内推才可以计算出全部的积分,故在实际计算中,我们采用反向传播方法,从最外层函数开始,即整个网络的最尾端。
这是对于一个输入-输出对而言,在实际网络中,我们通过是对一个batch的数据进行更新,这时便是对一个batch中的数据对进行求和,即 C ( w ) = 1 n ∑ C i ( w ) C(w)=\frac{1}{n}\sum C_i(w) C(w)=n1∑Ci(w),其中每一个 C i ( w ) C_i(w) Ci(w)对于一个 C ( y i , g ( x i ) ) C(y_i,g(x_i)) C(yi,g(xi))。
在更新参数时,定义
w : = w − η ∇ C ( w ) w:=w-\eta \nabla C(w) w:=w−η∇C(w)
这里 η ∇ C ( w ) \eta \nabla C(w) η∇C(w)便是上面微分计算出来的结果, η \eta η表示学习率,通过上一轮的参数减去计算得到的值,最终得到新的参数w
这便是整个反向传播和参数更新的过程
Pytorch代码学习
螺旋分类整体思考
通过对比线性模型和添加非线性变化ReLU激活函数模型,可以最终看到添加非线性激活函数可以有效解决非线性问题,这也体现了非线性激活函数在神经网络的一个重要作用,如果只有线性部分则整个神经网络无法学习到复杂的特征。
实验对比
对于线性模型,整个分类器代码如下:
model = nn.Sequential(
nn.Linear(D, H),
nn.Linear(H, C)
)
可以看到,整个分类器仅仅进行了线性变化,将特征维度从2升至100再将为最终的结果3,最后输出结果也显示仅仅通过线性变化对这种非线性问题难以学习到精准特征

之后尝试添加非线性激活函数ReLU,模型代码如下
model = nn.Sequential(
nn.Linear(D, H),
nn.ReLU(),
nn.Linear(H, C)
)
这里可以看到,与线性模型相比仅通过添加非线性激活函数,最终结果准确率从50%上升至92%。结果如下:
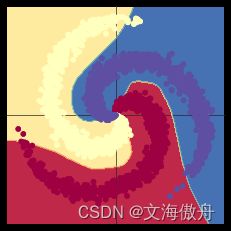
继续实验
在此基础上,如果通过更改激活函数,查看准确率是否会提示,我们尝试几种比较常见的激活函数–Sigmoid、Tanh作为对象
如果更改激活函数为sigmoid函数,即模型变为:
model = nn.Sequential(
nn.Linear(D, H),
nn.Sigmoid(),
nn.Linear(H, C)
)
发现最终效果并不理想,其准确率只有51%,最终显示结果为

可以发现其和普通线性模型并无明显优势
猜测其中原因为Sigmoid激活函数出现了梯度消失的问题,导致模型无法收敛,这也时ReLU函数优于Sigmoid函数的一大优势,ReLU函数在一般情况下较Sigmoid函数收敛更快
通过输出模型训练过程可以发现损失函数下降极其缓慢,准确率来说到在100轮训练时达到50%后到最后第1000轮准确率基本没有上升,说明模型训练无法收敛。
如果选择Tanh函数作为实验对象,可以发现最终准确率达到84.8%,好于Sigmoid函数但低于ReLU激活函数,其表现结果为