C/C++数据结构（四） —— 栈

---

什么是栈

假如有⼀个⼜细⼜⻓的圆筒，圆筒⼀端封闭，另⼀端开⼝。往圆筒⾥放⼊乒乓球，先放⼊的靠近圆筒底部，后放⼊的靠近圆筒⼊⼝。

那么，要想取出这些乒乓球，则只能按照和放⼊顺序相反的顺序来取，先取出后放⼊的，再取出先放⼊的，⽽不可能把最⾥⾯最先放⼊的乒乓球优先取出。

栈（stack）是⼀种线性数据结构，它就像⼀个上图所⽰的放⼊乒乓球的圆筒容器，栈中的元素只能先⼊后出 （First In Last Out，简称 FILO ）。

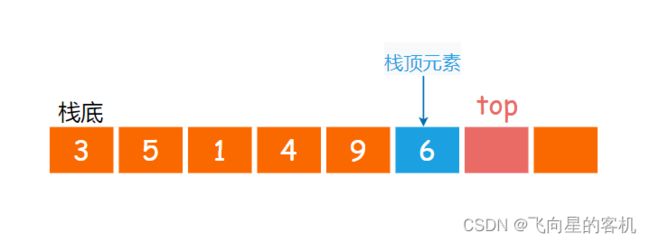
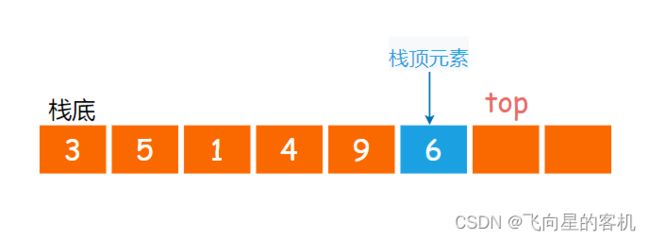
最早进⼊的元素存放的位置叫作 栈底 （bottom），最后进⼊的元素存放的位置叫作 栈顶 （top）。

栈的结构

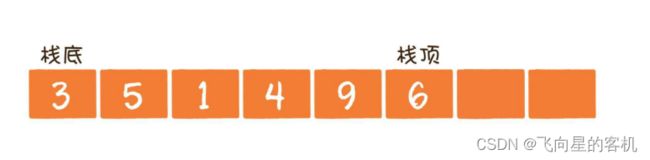
栈： 一种特殊的线性表，其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端
称为栈顶，另一端称为栈底。栈中的数据元素遵守 后进先出（Last In First Out）的原则。

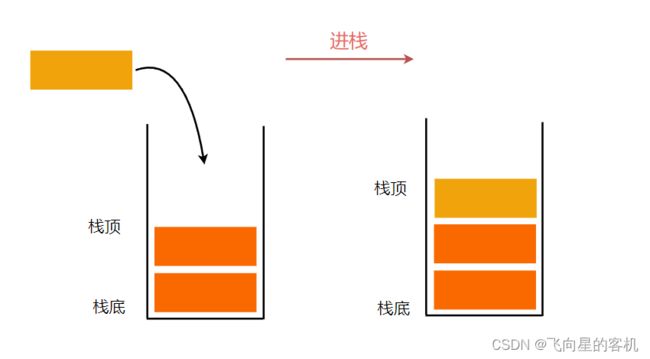
压栈： 栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶（如图所示）。

出栈： 栈的删除操作叫做出栈。出数据也在栈顶（如图所示）。

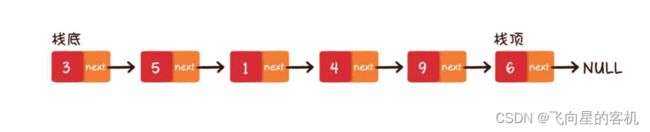
栈这种数据结构既可以⽤ 数组 来实现，也可以⽤ 链表 来实现。

栈的数组实现如下

栈的链表实现如下

1. 初始化栈

栈可以使用数组或者链表实现，相对而言 数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小。

首先，我们需要用 结构体 创建一个 栈，这个结构体需要包括栈的基本内容（栈，栈顶，栈的容量）。

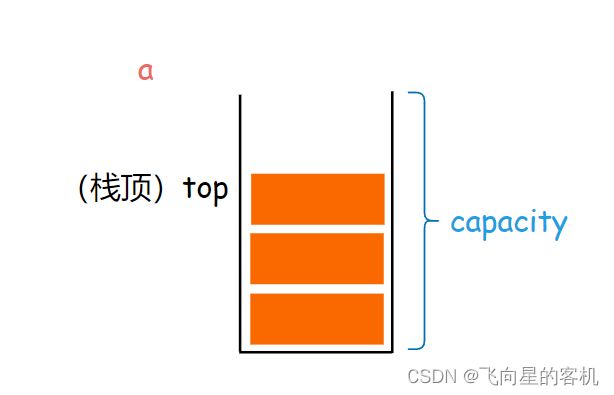
代码示例

// 支持动态增长的栈
typedef struct Stack
{
	STDataType* a; //栈
	int top; //栈顶
	int capacity; //容量
}ST;

然后，我们对创建好的 栈 进行初始化。

代码示例

//初始化栈
void StackInit(ST* ps) {
	assert(ps);
	ps->a = NULL;
	ps->top = 0; // 如果top初始化的时候为0，那么它表示栈顶元素的最后一个位置
	ps->capacity = 0;
}

注意： 这里对栈顶的初始化其实有 2 种定义；

（1）如果把 top 初始化为 0，那么它表示 栈顶元素的最后一个位置。（先放数据再加加）

（2）如果把 top 初始化为 -1，那么它表示 栈顶元素。（先加加再放数据）

2. 入栈

⼊栈操作（push）就是把新元素放⼊栈中，只允许从栈顶⼀侧放⼊元素，新元素的位置将会成为新的栈顶（如图所示）。

动图演示

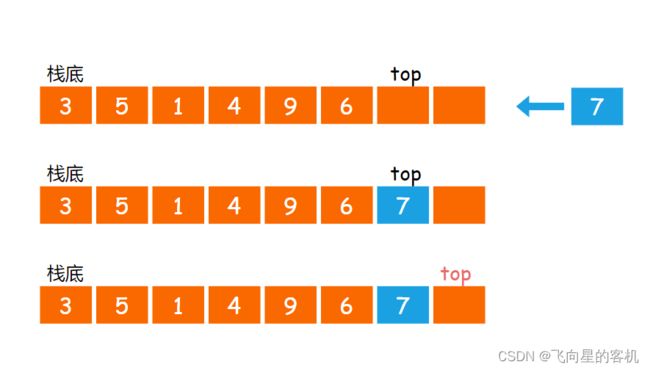
代码示例

//入栈
void StackPush(ST* ps, STDataType x) {
	assert(ps);

	//满了扩容
	if (ps->top == ps->capacity) { // 当top等于capacity的时候，就需要扩容

		/*capacity第一次等于0，然后直接扩到4；第二次进来，直接扩2倍*/
		int newCapacity = ps->capacity == (0) ? (4) : (ps->capacity * 2);

		/*realloc是要给总空间的大小*/
		ps->a = (STDataType*)realloc(ps->a, newCapacity * sizeof(STDataType));
		/*检查是否扩容成功*/
		if (ps->a == NULL) {
			printf("realloc fail\n");
			exit(-1);
		}
		ps->capacity = newCapacity;
	}
	ps->a[ps->top] = x; // 栈顶位置存放元素x
	ps->top++; // 然后top再指向下一个位置

	/*简化*/
	//ps->a[ps->top++];
}

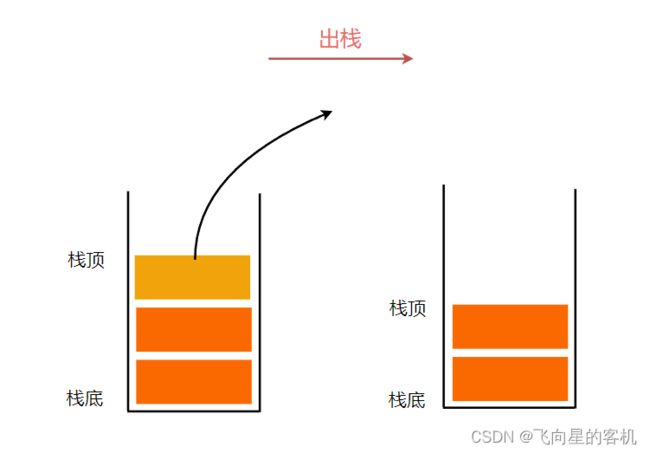
3. 出栈

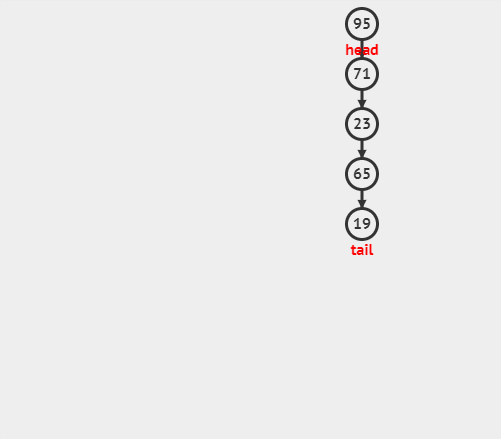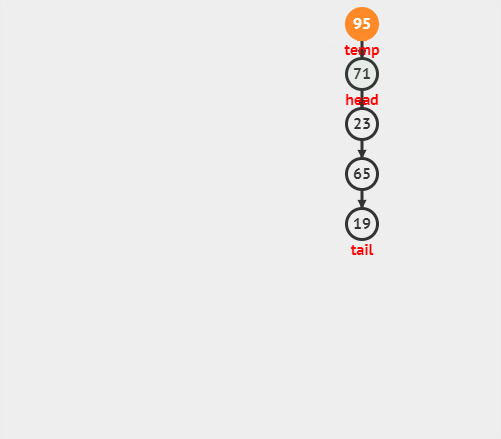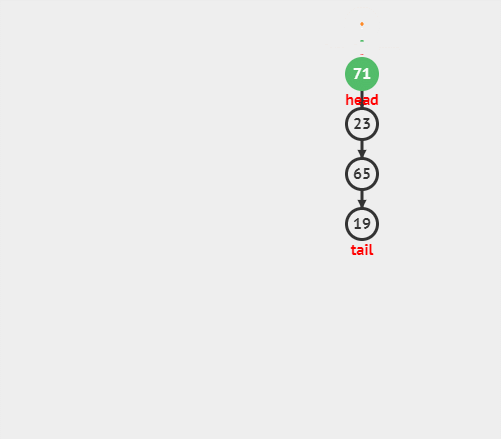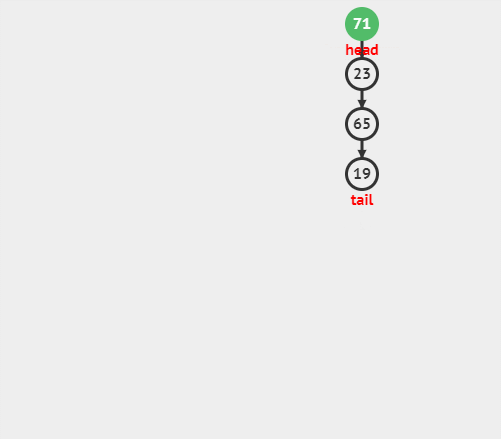
出栈操作（pop）就是把元素从栈中弹出，只有栈顶元素才允许出栈，出栈元素的前⼀个元素将会成为新的栈顶。

动图演示

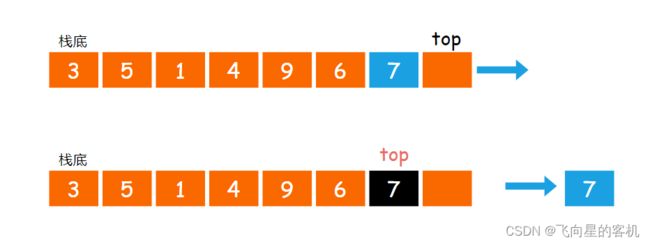
代码示例

//出栈
void StackPop(ST* ps) {
	assert(ps);
	assert(ps->top > 0); //出栈之前，要确保top不为空
	--ps->top; // 栈顶向前移
}

4. 获取栈顶元素

栈顶元素，即获取栈的最上方的元素。若栈为空，则不能获取。

动图演示

代码示例

//获取栈顶元素
STDataType StackTop(ST* ps) {
	assert(ps);
	assert(ps->top > 0); //如果top为0，那么栈就为空了，所以top不能为0

	/*top是指向栈顶元素的后一个位置，top-1才是栈顶元素*/
	return ps->a[ps->top - 1];
}

5. 获取栈中有效元素个数

因为 top 是从 0 开始的，而 栈顶元素 又在 top 的前一个位置，所以 top 的值便是栈中有效元素的个数。

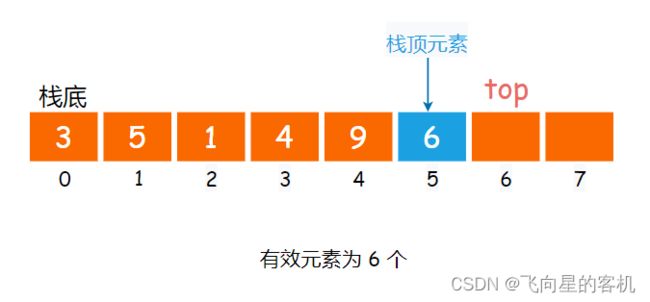
代码示例

// 获取栈中有效元素个数
int StackSize(ST* ps) {
	assert(ps);

	/*因为top是指向栈顶元素的最后一个位置
	假设元素为：1，2，3，4，5，那么top肯定是指向5的后一个位置
	又因为top是从0开始累加的，所以此时top肯定为5，刚好就是元素个数	
	*/
	return ps->top;
}

6. 检测栈是否为空

检测栈是否为空，即判断栈顶的位置是否是 0 即可。若栈顶是 0，则栈为空。

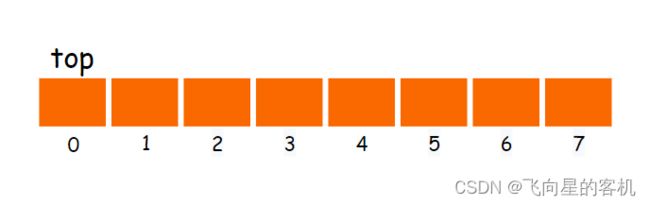
代码示例

//检测栈是否为空
bool StackEmpty(ST* ps) {
	assert(ps);
	
	return ps->top == 0; 
}

7. 销毁栈

因为栈的内存空间是 动态开辟 出来的，当我们使用完后必须释放其内存空间，避免内存泄漏。

代码示例

//销毁栈
void StackDestroy(ST* ps) {
	assert(ps);
	
	free(ps->a); // 释放栈
	ps->a = NULL; // 把栈置为空
	ps->top = 0; // 栈顶置0
	ps->capacity = 0; // 容量置0
}

8. 总结

栈的实现代码总体来说比较简单。

⼊栈和出栈只会影响到最后⼀个元素，不涉及其他元素的整体移动，所以⽆论是以数组还是以链表实现，⼊栈、出栈的时间复杂度都是 $O(1)$ 。

栈的应用：

栈的输出顺序和输⼊顺序相反，所以栈通常⽤于对 “历史” 的回溯，也就是逆流⽽上追溯 “历史”。
 
例如实现递归的逻辑，就可以⽤栈来代替，因为栈可以回溯⽅法的调⽤链。
 

 
栈还有⼀个著名的应⽤场景是⾯包屑导航，使⽤户在浏览⻚⾯时可以轻松地回溯到上⼀级或更上⼀级⻚⾯。
 

接口函数贴图

最后附上一张完整的 双向链表 的 接口函数图