数据结构与算法(五)--链表概念以及向链表添加元素
一、前言
今天我们学习另一种非常重要的线性数据结构–链表,之前我们已经学习了三种线性数据结构,分别是动态数组,栈和队列。其中队列我们额外学习了队列的另一种实现方式–循环队列。其实我们自己实现过前三个数据结构就知道,它们底层均依托静态数组,靠resize解决固定容量问题。而链表和前三种均不同,它是真正的动态数据结构。
学好链表,有利于:
- 链表是最简单的动态数据结构,方便你学习后面的二分搜索树,Trie,AVL,红黑树等等
- 更深入的理解引用(或者指针)
- 更深入的理解递归
- 辅助生成其他数据结构,例如我们之前学习的栈,队列可以通过链表实现,亦或是其他复杂的数据结构如图,哈希表等
二、链表
- 数据存储在"节点"(Node)中
class Node<T>{
T t; //数据
Node next; //指向当前节点的下一个节点
}
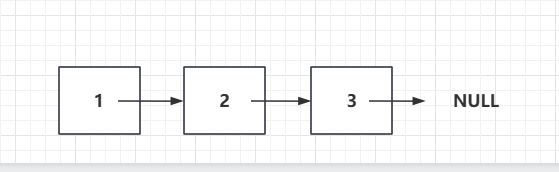
就像火车一样,每一个节点就像一个个车厢,车厢除了人(数据),还要和其他车厢进行连接,以使得数据是整合在一起的,用户可以方便的在所有的数据上进行查询等其他操作。而数据和数据之间的连接就是靠Node next决定的。

而我们的链表自然也不可能是无穷无尽的,我们链表存储的数据一定是有限的,那么最后一个节点它的next存储的就是一个NULL:我们也可以反过来得知,如果一个节点的NEXT是NULL,那么就说明这个节点一定是最后一个节点。
- 优点:真正的动态,不需要处理固定容量的问题,需要多少数据,就生成多少节点,并将它们连接起来。不需要像静态数组一样事先预定好一块儿固定空间。
- 缺点:丧失了随机访问的能力,说白了就是不能像数组一样直接拿一个索引,找出索引对应的元素。这是因为从底层机制上,数组所开辟的空间在内存里是连续分布的,所以我们可以直接去寻找索引对应的偏移,直接计算机相应的数据所存储的地址,直接用O(1)的复杂度就把这个元素找出来。但是链表不同,链表是靠next一层一层连接的,所以在计算机的底层每一个节点在内存的位置是不同的,我们必须靠next一点一点的找到我们想要的元素,这就是链表最大的缺点。
基于上述理论,我们可以有如下数组和链表的对比:
数组
- 数组最好用于索引有语意的情况。如scores[2]
- 最大的优点:支持快速查询
链表
- 链表不适合用于索引有语意的情况
- 最大的优点:动态
但是其实我们后续实现动态数组有说过,我们处理的都是索引没有语意的情况,对于这类不方便使用索引的数据,我们使用链表存储这些数据是更合适的。由于它最大的优点就是动态。
我们可以先初步搭建一下我们链表的类,首先创建一个链表类,然后创建一个内部私有类Node节点,就和我们之前提的是一样的:
public class LinkedList<T> {
//只有在链表结构内才能访问Node,链表结构外用户无法访问,因为对于用户而言,他们不需要指定链表的底层实现
private class Node {
public T data;
public Node next;
public Node(T data, Node next) {
this.data = data;
this.next = next;
}
public Node(T data) {
this(data, null);
}
public Node() {
this(null, null);
}
@Override
public String toString() {
return data.toString();
}
}
}
三、向链表添加元素
对于链表来说,我们要想访问链表中的所有节点,相应的必须把链表头存储起来,通常呢,链表的头结点叫作head,所以我们的LinkedList类中应该有一个Node类型的变量叫作head。它指向链表中的第一个节点。我们首先把我们linkedList的基础变量声明出来。
private Node head;
private int size;
public LinkedList() {
this.head = null;
this.size = 0;
}
public int getSize(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
①往链表头部增加元素
我们之前学习数组添加元素的时候,第一个说的方法是往数组末尾添加元素,这是因为对于数组而言,往数组末尾添加元素是比较方便的。
但链表则正好相反,对于链表而言往连边头部增加元素是非常方便的。
这其实很好理解,因为数组有size这个变量,它直接指向的是第一个未被添加元素的位置,所以直接往尾部添加很方便,因为有size这个变量在跟踪数组的尾巴。
而链表我们有头部的变量,但是我们没有相应的变量去跟踪链表的尾巴,所以我们往链表头添加元素很方便。
例如我现在要插入一个666的节点,图示如下:

往链表头添加元素后,我们要把这个元素和链表连接起来,所以我们需要让新添加的Node指向我们的head,然后由于连起来后,这个链表已经成了新的头节点,所以我们要把新添加的Node赋值给我们的头结点。
node.next = head;
head = node;
那么我们往头部插入元素实现就很简单:
public void addFirst(T t){
//声明一个新的节点,将这个新节点指向我们的头结点,然后再让新的节点成为头结点
Node node = new Node(t);
node.next = head;
head = node;
size ++;
}
其实上面的方法我们还有更优雅的写法:
public void addFirst(T t){
//声明一个新的节点,将这个新节点指向我们的头结点,然后再让新的节点成为头结点
// Node node = new Node(t);
// node.next = head;
// head = node;
//这一行代码干了上面三行代码的事
head = new Node(t,head);
size ++;
}
②往链表中间插入元素(注:这个操作不是常用操作,练习用)
例如,往“索引”为2的位置插入元素:
注意,这里索引打了引号,因为链表其实不存在索引这个概念,如下图,其实就相当于在1这个元素后面插入一个666的元素:

那么我们的思路就是,想要插入这个666的元素,需要找到插入的位置的前一个节点的位置,让这个节点的next指向我要插入的新节点,然后新节点的next指向原来的前一个节点的next的节点。所以我们为了方便找到前一个节点的位置,我们定义一个prev变量,初始情况prev和head指向同一个位置,而后面通过将prev移动找到对应的插入的位置的前一个节点的位置:

所以我们的任务就是找到插入666之前的那个节点是谁。比如我们现在要插入的位置是“索引”为2,所以插入之前的“索引”为1,所以我们遍历一下,prev指向“索引”为1的位置,然后新的节点的next指向我们的原来“索引”为1的next,即“索引”为2的节点,然后将原来“索引”为1的next指向我们新的节点:

node.next = prev.next;
prev.next= node;
关键就是:找到要添加的节点的前一个节点
有些人可能会注意到,当我要把元素添加到索引为0的位置的时候,此时索引为0的位置是没有前一个元素的,我们需要特殊处理一下。
然后就是对于链表很重要的一点:顺序
如果我把上述操作倒过来:
prev.next= node;
node.next = prev.next;
那么就会出现Node的next指向Node自己的错误,所以顺序一定要注意。可以通过纸笔或者debug调试一下。那么我们的实现如下:
//在链表的Index(0-based)位置添加新的元素e
public void add(T t, int index) {
if (index < 0 || index > size) {
throw new IllegalArgumentException("add element error:index should >= 0 && index <= size");
}
//如果Index = 0,由于索引为0的位置没有前一个元素,所以我们直接特殊处理,其实就相当于往头部添加元素
if(index == 0){
addFirst(t);
}else {
Node prev = head;
for(int i = 0;i < index - 1;i ++){
prev = prev.next;
}
Node node = new Node(t);
node.next = prev.next;
prev.next = node;
size ++;
}
}
那么add完成了后,我们就可以很简单的完成再添加一个add方法了,就是向链表末尾添加一个元素addLast(),其实就是add方法的index传size即可:
public void addLast(T t){
add(t,size);
}
那么以上就是链表的添加元素方法,但其实我们的add()仍然不够优雅,关键在于我们需要对Index=0的处理方法特殊处理,其实有一种方法可以直接让我们拜托这种特殊处理,就是设立虚拟head结点,这个我们后面会讲到:
四、为链表设立虚拟头结点
我们之前说add方法的时候,有一个不太优雅的地方就是当Index=0的时候,我们需要特殊处理,原因就是头结点没有上一个节点,那么解决思路也很简单,我们就造一个虚拟的链表头结点,它其实不存储任何的元素,我们将这个NULL节点称之为我们链表的head,也叫做dummyHead,即虚拟头结点。它其实就是索引为0对应的元素的前一个位置。那么这样添加,当index = 0时,就不需要特殊处理了。
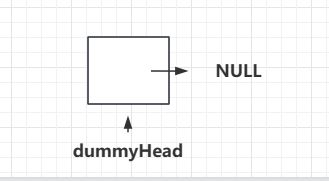
我们之前定义head节点是直接定义成NULL,但是现在我们的虚拟头结点就不单单是NULL了,而是一个节点,指向NULL。
private Node dummyHead;
private int size;
public LinkedList() {
dummyHead = new Node(null, null);
this.size = 0;
}
且我们现在prev是从dummyHead开始,即索引为0对应的元素的前一个位置开始,那么我们其实我们不再需要遍历Index-1次,而直接遍历Index次就可以找到插入位置的前一个位置了,说白了就是我的起点往前挪了一个位置,那么我遍历次数自然就需要少1次:

代码如下:
//在链表的Index(0-based)位置添加新的元素e
public void add(T t, int index) {
if (index < 0 || index > size) {
throw new IllegalArgumentException("add element error:index should >= 0 && index <= size");
}
Node prev = dummyHead;
for (int i = 0; i < index; i++) {
prev = prev.next;
}
Node node = new Node(t);
node.next = prev.next;
prev.next = node;
size++;
}
那么反过来,我们的addFirst也可以通过add简化了:
public void addFirst(T t) {
//声明一个新的节点,将这个新节点指向我们的头结点,然后再让新的节点成为头结点
add(t, 0);
}