Leetcode接雨水系列问题

目前遇到的有以下相似题目，后续会持续更新......

Leetcode11. 盛最多水的容器

Leetcode42. 接雨水

一、Leetcode11题：盛最多水的容器

1.题目描述

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i,height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例1：

输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/container-with-most-water

2.思路分析

设两指针 i， j ，指向的水槽板高度分别为 h[i]h[i] ，此状态下水槽面积为 S(i, j)。由于可容纳水的高度由两板中的 短板 决定，因此可得如下 面积公式 ：

在每个状态下，无论长板或短板向中间收窄一格，都会导致水槽 底边宽度 −1​ 变短：

若向内 移动短板 ，水槽的短板 min(h[i], h[j]) 可能变大，因此下个水槽的面积 可能增大 。
若向内 移动长板 ，水槽的短板 min(h[i], h[j])不变或变小，因此下个水槽的面积 一定变小 。
因此，初始化双指针分列水槽左右两端，循环每轮将短板向内移动一格，并更新面积最大值，直到两指针相遇时跳出；即可获得最大面积。

算法流程：

• 初始化： 双指针 i , j 分列水槽左右两端；
• 循环收窄： 直至双指针相遇时跳出；

                更新面积最大值 res ；

                选定两板高度中的短板，向中间收窄一格；

• 返回值： 返回面积最大值 res 即可； 

3.解答

class Solution {
    //双指针

    public int maxArea(int[] height) {
        //定义双指针
        int i = 0, j = height.length - 1;
        //存储结果
        int res = 0;
        //遍历计算
        while(i < j){
            //容水量只与短板有关
            if(height[i] < height[j]){
                res = Math.max(res, height[i] * (j - i));
                //向内移动短板有可能让结果变大（移动板版结果一定变小）
                i++;
            }else{
                res = Math.max(res, height[j] * (j - i));
                j--;
            }
        }

        return res;
    }
}

时间复杂度 O(N) ： 双指针遍历一次底边宽度 N​​ 。
空间复杂度 O(1)​ ： 变量 i ,j , res 使用常数额外空间。

 二、Leetcode42题：接雨水

1.题目描述

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例1：

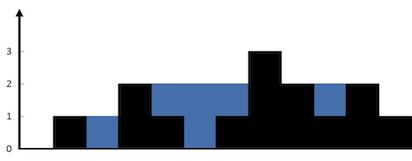
输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/trapping-rain-water

2.思路分析 

我们开两个数组 r_max 和 l_max 充当备忘录， l_max[i] 表⽰位置 i 左边最⾼的柱⼦⾼度，r_max[i] 表⽰位置 i 右边最⾼的柱⼦⾼度。预先把这两个数组计算好，避免重复计算。

然后遍历数组，计算当前位置的雨水量：

Nath.min(左边最高的柱子， 右边最高的柱子) - 当前柱子的高度

 3.解答

3.1 遍历解法

class Solution {
    //带备忘录的暴力解法

    public int trap(int[] height) {
        int n = height.length;
        if(n <= 1){
            return 0;
        }

        //定义两个数组，分别存储height[0,,,i]和height[i,,,n - 1]的最大值
        int[] leftMaxNum = new int[n];
        int[] rightMaxNum = new int[n];
        //初始化
        leftMaxNum[0] = height[0];
        rightMaxNum[n - 1] = height[n - 1];
        //计算i左侧的最大值
        for(int i = 1; i < n; i++){
            leftMaxNum[i] = Math.max(leftMaxNum[i - 1], height[i]);
        }
        for(int j = n - 2; j >= 0; j--){
            rightMaxNum[j] = Math.max(rightMaxNum[j + 1], height[j]);
        }

        //遍历计算每个位置能接住的雨水量
        int res = 0;
        for(int k = 1; k < n - 1; k++){
            res += Math.min(leftMaxNum[k], rightMaxNum[k]) - height[k];
        }

        return res;
    }
}

 3.2 双指针解法

class Solution {
    //3.双指针技巧，边走边算，降低时间复杂度和空间复杂度

    public int trap(int[] height) {
        int n = height.length;
        int ans = 0;
        //左右指针
        int left = 0;
        int right = n - 1;
        //初始化
        int l_max = height[0];
        int r_max = height[n - 1];
        //从两边向中间计算
        while(left <= right){
            l_max = Math.max(l_max, height[left]);
            r_max = Math.max(r_max, height[right]);

            if(l_max < r_max){
                ans += l_max - height[left];
                left++;
            }else{
                ans += r_max - height[right];
                right--;
            }
        }
        return ans;
    }
}