Python数据分析(01) 绘制三维曲面图像
目录
- 前言
- 绘制步骤
-
- 包依赖
- 定义画布和坐标轴
- 根据函数生成数据
- 作图
- 结果展示
前言
图像便于展示自己的研究成果,或作为研究步骤用于分析结论、提供灵感。下面介绍python3绘制三维曲面图的步骤。
绘制步骤
包依赖
绘制三维曲面图,依赖下面两个包。numpy, matplotlib
import numpy as np
from matplotlib import pyplot as plt
定义画布和坐标轴
使用plt.figure()生成一个下标为1的画布。
使用plt.axes(projection='3d')生成一个三维的坐标轴,以控制三维数据在坐标轴上绘制。如果不指定参数为3d,返回二维坐标轴。
fig = plt.figure()
ax = plt.axes(projection="3d")
根据函数生成数据
一般根据自己的需要,选定一个三维空间上的二元函数 z = f ( x , y ) z=f(x,y) z=f(x,y)。在我的另一篇博文机器学习(2) 感知机原理及实现中,选定了一个峰值函数用于展示山峰的形状,借以理解梯度下降法的含义。峰值函数选自于matlab的peaks演示函数,该函数的表达式为:
z = 3 ( 1 − x ) 2 e − x 2 − ( y + 1 ) 2 − 10 ( x 5 − x 2 − y 5 ) e − x 2 − y 2 − 1 3 e − ( x + 1 ) 2 − y 2 \displaystyle{z=3(1-x)^2e^{-x^2-(y+1)^2}-10(\frac{x}{5}-x^2-y^5)e^{-x^2-y^2}-\frac{1}{3}e^{-(x+1)^2-y^2}} z=3(1−x)2e−x2−(y+1)2−10(5x−x2−y5)e−x2−y2−31e−(x+1)2−y2
首先生成X轴方向和Y轴方向的网格型数据。
x = y = np.arange(start=-4, stop=4, step=0.1)
X, Y = np.meshgrid(x, y)
上面这段代码用np.arange(start=-4,stop=4,step=0.1)生成从-4开始到4结束,步长为0.1的80个数据。也就是说,希望在80 × \times × 80的6400个坐标点上分别计算坐标点的函数值并赋给Z。用于生成这6400个点的函数就是np.meshgrid(x,y),mesh是网,grid是格,意思是根据坐标向量生成网格中心点的坐标。这样经过转换X.size()==6400, Y.size()==6400, (Xi, Yi)=(X[i],Y[i])。接下来只需要根据生成函数,代入每个点的X轴、Y轴坐标即可。
Z = 3 * (1-X)**2 * np.exp(-X**2-(Y+1)**2)- 10 * (X/5- X**3 - Y**5)*np.exp(-X**2-Y**2)-1/3*np.exp(-(X+1)**2-Y**2)
作图
利用坐标轴的ax.plot_surface(X,Y,Z)功能即可将6400个坐标绘制成一个平滑的曲线。该函数有其他参数,如alpha=0.9控制曲线的透明度为90%;cstride=2column stride控制列数据每间隔2个点拟合一个平滑的曲线,rstride=2row column控制行数据每间隔2个点拟合一个平滑的曲线,cstride,rstride设置的数值越小,则曲线越贴合给定的数据;cmap='rainbow'控制图像的着色方式为彩虹色,z的数值越大,颜色更偏向于暖色系,z数值越小,颜色更偏向于深色系,cmap还可以等于'cool','winter','YlGnBu'等。
ax.plot_surface(X,Y,Z,alpha=0.9, cstride=1, rstride = 1, cmap='rainbow')
plt.show()
结果展示
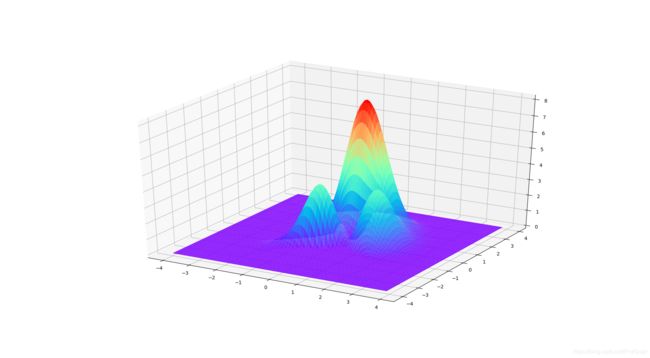
- 山峰函数的全貌。
import numpy as np
from matplotlib import pyplot as plt
fig = plt.figure()
ax = plt.axes(projection="3d")
x = y = np.arange(start=-4, stop=4, step=0.1)
X, Y = np.meshgrid(x, y)
Z = 3 * (1-X)**2 * np.exp(-X**2-(Y+1)**2)- 10 * (X/5- X**3 - Y**5)*np.exp(-X**2-Y**2)-1/3*np.exp(-(X+1)**2-Y**2)
ax.plot_surface(X,Y,Z,alpha=0.9, cstride=1, rstride = 1, cmap='rainbow')
plt.show()
- 山峰函数上半轴
import numpy as np
from matplotlib import pyplot as plt
fig = plt.figure()
ax = plt.axes(projection="3d")
x = y = np.arange(start=-4, stop=4, step=0.1)
X, Y = np.meshgrid(x, y)
Z = 3 * (1-X)**2 * np.exp(-X**2-(Y+1)**2)- 10 * (X/5- X**3 - Y**5)*np.exp(-X**2-Y**2)-1/3*np.exp(-(X+1)**2-Y**2)
Z[Z<0]=0
ax.plot_surface(X,Y,Z,alpha=0.9, cstride=1, rstride = 1, cmap='rainbow')
plt.show()
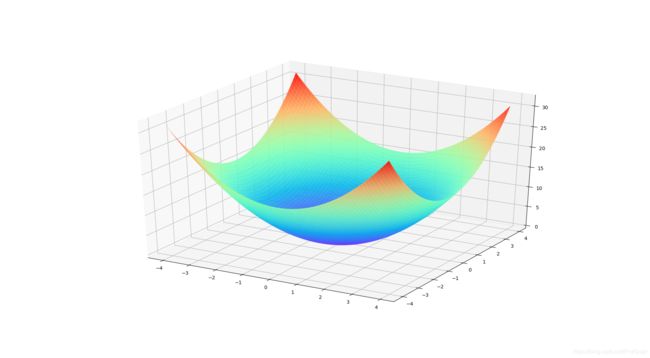
- 倒锥形曲面(倒山峰形)
import numpy as np
from matplotlib import pyplot as plt
fig = plt.figure()
ax = plt.axes(projection="3d")
x = y = np.arange(start=-4, stop=4, step=0.1)
X, Y = np.meshgrid(x, y)
Z = X**2+Y**2
ax.plot_surface(X,Y,Z,alpha=0.9, cstride=1, rstride = 1, cmap='rainbow')
plt.show()