如何利用Arcgis进行地统计学分析（三）：如何利用arcgis进行地统计插值，克里金插值（Kriging）

一、克里金插值介绍

克里金（克里格）方法（Kriging）又称空间局部插值法，是以变异函数理论和结构分析为基础，在有限区域内对区域化变量进行无偏最优估计的一种方法，是地统计学的主要内容之一。

    克里金方法的适用范围为区域化变量存在空间相关性，即如果变异函数和结构分析的结果表明区域化变量存在空间相关性，则可以利用克里格方法进行内插或外推；否则，是不可行的。其实质是利用区域化变量的原始数据和变异函数的结构特点，对未知样点进行线性无偏、最优估计。无偏是指偏差的数学期望为 0，最优是指估计值与实际值之差的平方和最小。也就是说，克里金方法是根据未知样点有限邻域内的若干已知样本点数据，在考虑了样本点的形状、大小和空间方位，与未知样点的相互空间位置关系，以及变异函数提供的结构信息之后，对未知样点进行的一种线性无偏最优估计。

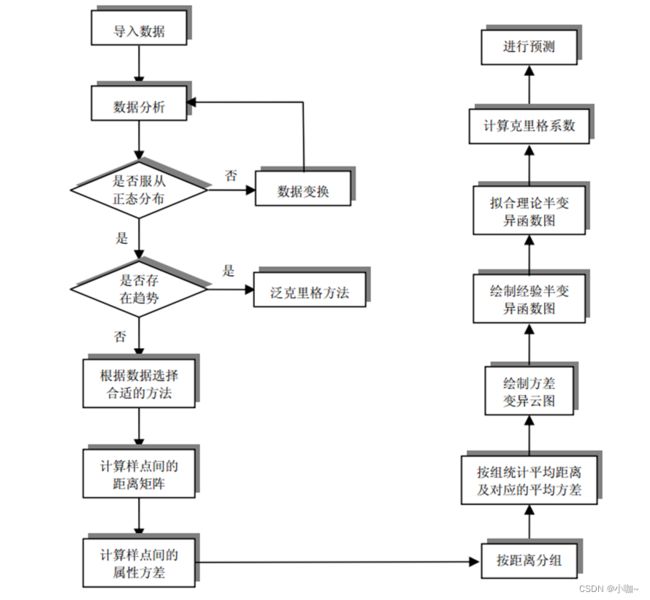
用克里格方法进行插值的主要步骤

在克里格插值过程中，需注意以下几点：

（1） 数据应符合前提假设。

（2） 数据应尽量充分，样本数尽量大于 80，每一种距离间隔分类中的样本对数尽量多于10 对。

（3） 在具体建模过程中，很多参数是可调的，且每个参数对结果的影响不同。如：块金值：误差随块金值的增大而增大；基台值：对结果影响不大；变程：存在最佳变程值；拟合函数：存在最佳拟合函数。

（4） 当数据足够多时，各种插值方法的效果相差不大。

二、不同克里金插值对比

1.普通克里格插值（Ordinary Kriging）

    普通克里格法是所有克里格插值方法中最基本、最重要、应用最广泛的插值方法。它的优点在于不仅考虑了各样本点的空间相关性，而且在给出待插点的估算值的同时，还给出表示估算精度的方差。

1. 点击“Geostatistical Analyst”工具条，选择“Geostatistical Wizard”。

2.在弹出的对话框中选择“Kriging/Cokriging”。

3.设置“Source Dataset”。

4.在对话框中选择“Ordinary Kriging”,在下面的选项中点击预测（Prediction）,点击 Next 按钮。

5. 设置“Show Search Direction”为“true”，移动左图中的搜索方向，然后单击 Next 按钮。

  6.在Searching Neighborhood窗口中，单击 Next 按钮。   

7.在Cross Validation窗口中，可查看“标准平均值（Mean Standardized）最接近于 0”等其他精度评价参数。

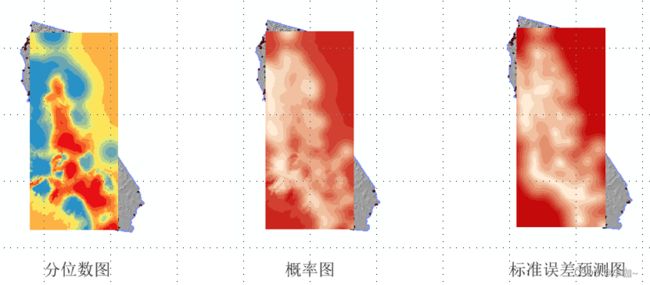
    同样，可以创建普通克里格分位数图（Quantile）、概率图（Probability）、标准误差预测图（Prediction Standard Error ）。

2.简单克里格插值（Simple Kriging）

    简单克里格是区域化变量的线性估计，它假设数据变化成正态分布，认为区域化变量 Z 的期望值为已知的某一常数。使用简单克里格创建分位数图（Quantile）、概率图（Probability）、标准误差预测图（Prediction Standard Error ）

3.泛克里格插值（Universal Kriging）

    普通克里金插值法要求区域化变量满足二阶平稳假设或固有假设，但实际应用中这一假设往往无法满足，从而限制了普通克里金法的应用。泛克里金的引入解决了这个问题。 

    使用泛克里格创建预测图（Prediction）、分位数图（Quantile）、概率图（Probability）、标准误差预测图（Prediction Standard Error ），结果如下。

4.指示克里格插值（Indicator Kriging）

    指示克里格法是一种非参数方法，无需了解数据的分析类型，该方法的特点是可以将异常值对插值的影像降到最低，因此也是常用的方法之一。

    使用指示克里格创建概率图（Probability）、标准误差预测图（Prediction Standard Error ），结果如下：

5.概率克里格插值（Probability Kriging）

    概率克里格法是指示克里格法的一种改进。它不仅具有指示克里金法的优点，即非参数和无分布特性，同时也减小了估计方差，提高了插值精度，降低了指示克里金法的平滑作用。

    使用概率克里格创建概率图（Probability）、标准误差预测图（Prediction Standard Error ）

6.析取克里格插值（Disjunctive Krigin)

析取克里金法对数据的要求较为严格，数据需服从二元正态分布，并且计算过程也较为复杂，所以尽管一般情况下析取克里金法比普通克里金法的预测效果更佳，但使用时需要谨慎。它可以创建预测图、概率图、预测标准误差图和标准误差指示图。 

    使用析取克里格创建预测图（Prediction）、分位数图（Quantile）、概率图（Probability）、标准误差预测图（Prediction Standard Error ）结果如下。