Matlab之数据归一化函数——mapminmax()

归一化化就是要把你需要处理的数据经过处理后（通过某种算法）限制在你需要的一定范围内。首先归一化是为了后面数据处理的方便，其次是保证程序运行时收敛加快。

mapminmax函数
这个函数可以把矩阵的每一行归一到[-1 1]. [y1,PS] = mapminmax(x1). 其中x1 是需要归一的矩阵 y1是结果。

函数接口：
[Y,PS] = mapminmax(X)
[Y,PS] = mapminmax(X,FP)
Y = mapminmax(‘apply’,X,PS)
X = mapminmax(‘reverse’,Y,PS)

算法原理：
假设X仅具有有限的实数值，并且每行的元素并非全部相等。如果有一行的元素都相同比如xt = [1 1 1],此时xmax = xmin = 1,把此时的变换变为y = ymin,matlab内部就是这么解决的.否则该除以0了,没有意义!

• y = (ymax-ymin)*(x-xmin)/(xmax-xmin) + ymin;
• 特殊情况下：y=ymin；

案例1：特殊情况

案例2：验证映射

x1=[1,2,3]；
[y,ps] = mapminmax(x1)；

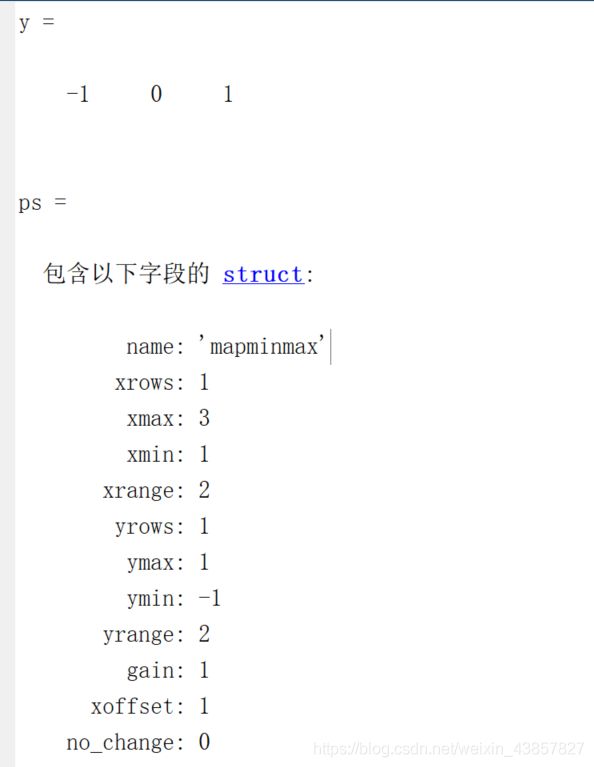
x1 = [1 2 3]，由图可知：对于x1而言 xmin = 1,xmax = 3;ymax=1，ymin=-1
采用这个映射 f: 2*(x-xmin)/(xmax-xmin)+(-1)。
则y(1) = 2*(1 - 1)/(3-1)+(-1) = -1;
y(2) = 2*(2 - 1)/(3-1)+(-1) = 0;
y(3) = 2*(3-1)/(3-1)+(-1) = 1;

对于上面算法中的映射函数 其中ymin,和ymax是参数,可以自己设定,默认为-1,1;

案例3：修改参数

ps.ymin=0;
x1=[1 2 3];
[y,ps]=mapminmax(x1,ps)

y(1) = (1-0)*(1 - 1)/(3-1)+0= 0;
注意：括号里的ps必需加上，不然还是默认参数。

如果我对x1 = [1 2 3]采用了某种规范化的方式, 现在我要对x2 = [4 5 6]采用同样的规范化方式[同样的映射],如下可办到:

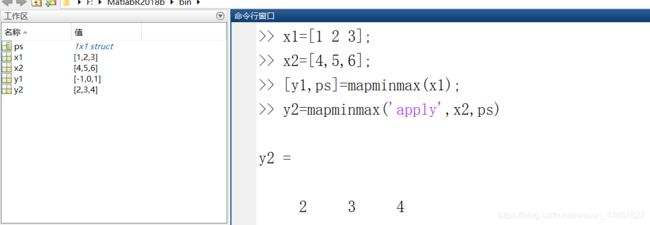
即对x1采用的规范化映射为: f:（1-（-1））*(x-1)/(3-1)+(-1),(记录在ps中),对x2也要采取这个映射.
x2 = [4 5 6],用这个映射我们来算一下.
y2(4) = 2(4-1)/(3-1)+(-1) = 2
y2(5) = 2(5-1)/(3-1)+(-1) =3
y2(6) = 2(6-1)/(3-1)+(-1) = 4
特别注意：用的是上一个的ps而不是自己的ps

X = mapminmax(‘reverse’,Y,PS)的作用就是进行反归一化,将归一化的数据反归一化再得到原来的数据: