有限元方法之三角形元任意阶的Lagrange型形状函数
文章目录
-
- 前言
- 求解区域
-
- 1. 一维
- 2. 二维
- 3. 三维
- 形状函数
- 三角形单元
-
- 面积坐标
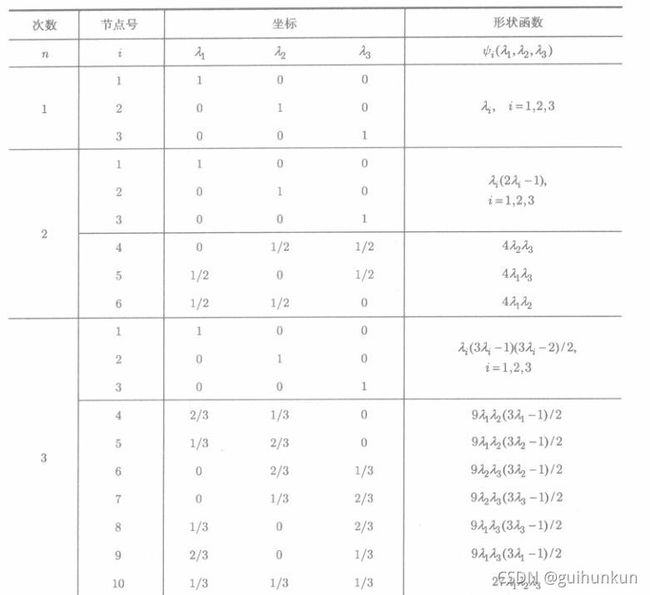
- 三角形单元的Lagrange型形状函数
- 三角形单元上Lagrange型形状函数的节点坐标
- 三角形单元Lagrange型形状函数关键汇总
前言
本文主要介绍Lagrange型形状函数在三角形单元上基函数公式和节点坐标公式的推导,以及相应的面积坐标相关知识。
求解区域
求解区域即偏微分方程所定义的区域,或者说几何形状。
1. 一维
一维元素多是线元即线段。相应元素节点可以取线段的两个端点,或者线段中点。
2. 二维
二维元素有三角形,矩形,四边形等。相应元素节点可以取多边形的顶点,或者边的中点,以及多边形的形心。
3. 三维
三维元素有四面体,五面体,三棱柱体,六面体等。
形状函数
形状函数一般采用多项式,一是计算方便;二是易于证明其收敛性,并要求多项式的次数与元素(单元)自由度匹配得当。
-
一维 k k k 次多项式 p k ( x ) = ∑ i = 0 T k ( 1 ) a i x i p_k(x) = \sum_{i=0}^{T_k^{(1)}} a_ix^i pk(x)=i=0∑Tk(1)aixi
其中 T k ( 1 ) = k + 1 T_k^{(1)} = k + 1 Tk(1)=k+1 是 p k ( x ) p_k(x) pk(x) 的项数。 -
二维 k k k 次多项式 p k ( x , y ) = ∑ m = 1 T k ( 2 ) a m x i y j i + j ≤ k p_k(x, y) = \sum_{m=1}^{T_k^{(2)}} a_mx^iy^j \ \ \ \ \ \ i+j \leq k pk(x,y)=m=1∑Tk(2)amxiyj i+j≤k
它的独立项数 T k ( 2 ) = 1 2 ( k + 1 ) ( k + 2 ) T_k^{(2)} = \frac{1}{2}(k + 1)(k+2) Tk(2)=21(k+1)(k+2) 。
二维 k k k次完全多项式自由度可以用如下一个三角形排列表示:
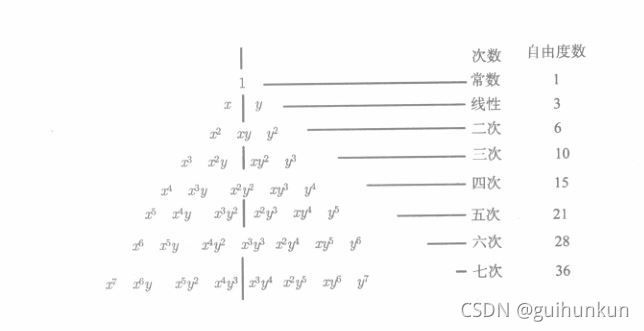
-
三维 k k k 次完全多项式 p k ( x , y , z ) = ∑ l = 1 T k ( 3 ) a l x i y j z m i + j + m ≤ k p_k(x, y, z) = \sum_{l=1}^{T_k^{(3)}} a_lx^iy^jz^m \ \ \ \ \ \ i+j+m \leq k pk(x,y,z)=l=1∑Tk(3)alxiyjzm i+j+m≤k
其中独立项数 T k ( 3 ) = ( k + 1 ) ( k + 2 ) ( k + 3 ) / 6 T_k^{(3)} = (k + 1)(k+2)(k+3)/6 Tk(3)=(k+1)(k+2)(k+3)/6 。
三维 k k k次多项式自由度可以排列成如下四面体形式:
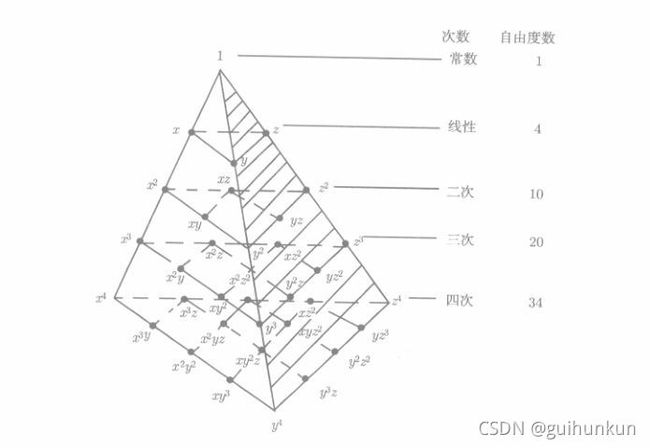
三角形单元
在二维问题中,三角形元素被广泛采用,除了它形状简单,随意性大,适应区域形状能力强的优点,当采用面积坐标后,三角形单元的形状函数生成简单,容易标准化。
面积坐标
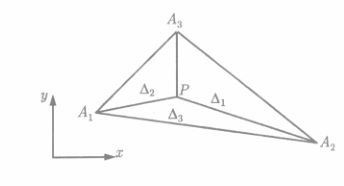
设任意三角形三个顶点 A 1 A_1 A1 A 2 A_2 A2 A 3 A_3 A3 按逆时针排列,三角形的面积为 Δ \Delta Δ。 取三角形内任一点 P ( x , y ) P(x, y) P(x,y),由点 P P P向三个顶点分别引直线,将三角形分割成三个三角形 P A 2 A 3 PA_2A_3 PA2A3, P A 3 A 1 PA_3A_1 PA3A1, P A 1 A 2 PA_1A_2 PA1A2。分别记相应的面积为 Δ 1 \Delta_1 Δ1, Δ 2 \Delta_2 Δ2, Δ 3 \Delta_3 Δ3,令
λ 1 = Δ 1 / Δ , λ 2 = Δ 2 / Δ , λ 3 = Δ 3 / Δ , ( 1 ) \lambda_1 = \Delta_1/ \Delta, \ \ \ \lambda_2 = \Delta_2/ \Delta, \ \ \ \lambda_3 = \Delta_3/ \Delta,\ \ \ \ \ \ \ \ \ \ \ \ (1) λ1=Δ1/Δ, λ2=Δ2/Δ, λ3=Δ3/Δ, (1)
称 λ i ( i = 1 , 2 , 3 ) \lambda_ i(i = 1, 2, 3) λi(i=1,2,3)为 P P P点的面积坐标,显然有
0 ≤ λ i ≤ 1 , λ 1 + λ 2 + λ 3 = 1 ( 2 ) 0 \leq \lambda_i \leq 1, \ \ \ \lambda_1 + \lambda_2 + \lambda3 = 1\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2) 0≤λi≤1, λ1+λ2+λ3=1 (2)
说明,三角形 A 1 A 2 A 3 A_1A_2A_3 A1A2A3内的任一点 P P P比对应一组数 λ i \lambda_i λi,它们满足(2)。反之,若给出三个数 λ i \lambda_i λi满足(2),则必能在三角形 A 1 A 2 A 3 A_1A_2A_3 A1A2A3内按(1)确定一个与之相应的 P P P点。
显然,三角形的三个顶点的面积坐标为 A 1 = ( 1 , 0 , 0 ) , A 2 = ( 0 , 1 , 1 ) , A 3 = ( 0 , 0 , 1 ) A_1 = (1, 0, 0), \ \ \ A_2 = (0, 1, 1), \ \ \ A_3 = (0, 0, 1) A1=(1,0,0), A2=(0,1,1), A3=(0,0,1)
若三角形三个顶点的直角坐标分别为 A 1 ( x 1 , y 1 ) , A 2 ( x 2 , y 2 ) , A 3 ( x 3 , y 3 ) A_1(x_1, y_1), A_2(x_2, y_2), A_3(x_3, y_3) A1(x1,y1),A2(x2,y2),A3(x3,y3),并记
a i = y i − y k , b i = − ( x j − x k ) c i = ∣ x j x k y j y k ∣ , i , j , k 按 1 , 2 , 3 轮 换 a_i = y_i-y_k, \ \ \ \ \ \ \ \ \ \ b_i = -(x_j-x_k) \\ c_i = \begin{vmatrix} x_j & x_k\\ y_j & y_k\end{vmatrix}, \ \ \ \ \ \ \ \ i, j, k 按1,2,3轮换 ai=yi−yk, bi=−(xj−xk)ci=∣∣∣∣xjyjxkyk∣∣∣∣, i,j,k按1,2,3轮换
记 D 0 = ∣ D ∣ D_0 = |D| D0=∣D∣, 其中 D = ∣ 1 1 1 x 1 x 2 x 3 y 1 y 2 y 3 ∣ = c 1 + c 2 + c 3 D = \begin{vmatrix} 1 & 1 & 1 \\ x_1 & x_2 & x_3\\ y_1 & y_2 & y_3 \end{vmatrix} = c_1 + c_2 + c_3 D=∣∣∣∣∣∣1x1y11x2y21x3y3∣∣∣∣∣∣=c1+c2+c3
那么面积坐标与直角坐标之间的关系为
λ i = ( a i x + b i y + c i ) / D 0 , i = 1 , 2 , 3. ( 3 ) \lambda_i = (a_ix + b_iy + c_i)/D_0, \ \ \ \ \ i = 1,2,3. \ \ \ \ \ \ \ \ \ (3) λi=(aix+biy+ci)/D0, i=1,2,3. (3)
或
{ x = ∑ i = 1 3 x i λ i y = ∑ i = 1 3 y i λ i λ 1 + λ 2 + λ + 3 = 1 ( 4 ) \left\{\begin{matrix} x = \sum_{i = 1}^3{x_i\lambda_i} \\ y = \sum_{i = 1}^3{y_i\lambda_i} \\ \lambda_1 + \lambda_2 + \lambda+3 = 1\\\end{matrix}\right. \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4) ⎩⎨⎧x=∑i=13xiλiy=∑i=13yiλiλ1+λ2+λ+3=1 (4)
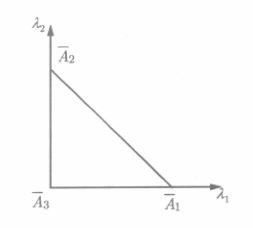
这是从 ( x , y ) (x, y) (x,y)平面到 ( λ 1 , λ 2 ) (\lambda_1, \lambda_2) (λ1,λ2)平面之间的映射关系,它将 ( x , y ) (x, y) (x,y)平面上任一三角形 A 1 A 2 A 3 A_1A_2A_3 A1A2A3映射到 ( λ 1 , λ 2 ) (\lambda_1, \lambda_2) (λ1,λ2)平面三角形 A 1 ˉ A 2 ˉ A 3 ˉ \bar{A_1}\bar{A_2}\bar{A_3} A1ˉA2ˉA3ˉ如下图所示,称 A 1 ˉ A 2 ˉ A 3 ˉ \bar{A_1}\bar{A_2}\bar{A_3} A1ˉA2ˉA3ˉ为标准三角形。
由于 ( x , y ) (x, y) (x,y)是 ( λ 1 , λ 2 , λ 3 ) (\lambda_1, \lambda_2, \lambda_3) (λ1,λ2,λ3)的函数, ( λ 1 , λ 2 , λ 3 ) (\lambda_1, \lambda_2, \lambda_3) (λ1,λ2,λ3)也是 ( x , y ) (x, y) (x,y)的函数,则导数有如下关系
[ ∂ ∂ λ 1 ∂ ∂ λ 2 ] = J [ ∂ ∂ x ∂ ∂ y ] , [ ∂ ∂ x ∂ ∂ y ] = J − 1 [ ∂ ∂ λ 1 ∂ ∂ λ 2 ] \begin{bmatrix} \frac{\partial}{\partial{\lambda_1}} \\ \frac{\partial}{\partial{\lambda_2}} \\\end{bmatrix} = J\begin{bmatrix} \frac{\partial}{\partial{x}} \\ \frac{\partial}{\partial{y}} \\\end{bmatrix}, \ \ \ \begin{bmatrix} \frac{\partial}{\partial{x}} \\ \frac{\partial}{\partial{y}} \\\end{bmatrix} = J^{-1}\begin{bmatrix} \frac{\partial}{\partial{\lambda_1}} \\ \frac{\partial}{\partial{\lambda_2}} \\\end{bmatrix} [∂λ1∂∂λ2∂]=J[∂x∂∂y∂], [∂x∂∂y∂]=J−1[∂λ1∂∂λ2∂]
其中 J J J为从 ( x , y ) (x, y) (x,y)到 ( λ 1 , λ 2 ) (\lambda_1, \lambda_2) (λ1,λ2)坐标变换的 J a c o b i Jacobi Jacobi矩阵。
J = [ ∂ x ∂ λ 1 ∂ y ∂ λ 1 ∂ x ∂ λ 2 ∂ y ∂ λ 2 ] = [ x 1 − x 3 y 1 − y 3 x 2 − x 3 y 2 − y 3 ] J = \begin{bmatrix} \frac{\partial x}{\partial{\lambda_1}} & \frac{\partial y}{\partial{\lambda_1}} \\ \frac{\partial x}{\partial{\lambda_2}} & \frac{\partial y}{\partial{\lambda_2}} \\\end{bmatrix} = \begin{bmatrix} x_1 - x_3 & y_1 - y_3 \\ x_2 - x_3 & y_2 - y_3 \\\end{bmatrix} J=[∂λ1∂x∂λ2∂x∂λ1∂y∂λ2∂y]=[x1−x3x2−x3y1−y3y2−y3]
三角形单元的Lagrange型形状函数
二元 n n n次多项式
P n ( x , y ) = ∑ i + j = 1 T n a i j x i y j ( 5 ) P_n(x,y) = \sum_{i+j=1}^{T_n}{a_{ij}x^iy^j} \ \ \ \ \ \ \ \ \ \ \ \ \ (5) Pn(x,y)=i+j=1∑Tnaijxiyj (5)
有 T n = 1 2 ( n + 1 ) ( n + 2 ) T_n = \frac{1}{2}(n+1)(n+2) Tn=21(n+1)(n+2)个自由度。若采用自然坐标即面积坐标 Λ = ( λ 1 , λ 2 , λ 3 ) \Lambda = (\lambda_1, \lambda_2, \lambda_3) Λ=(λ1,λ2,λ3)且 α = ( α 1 , α 2 , α 3 ) ∈ Z + 3 \alpha = (\alpha_1, \alpha_2, \alpha_3) \in Z_{+}^3 α=(α1,α2,α3)∈Z+3 那么
P n ( λ 1 , λ 2 , λ 3 ) = ∑ ∣ α ∣ = n A α λ 1 α 1 λ 2 α 2 λ 3 α 3 ( 6 ) P_n(\lambda_1, \lambda_2, \lambda_3) = \sum_{\left | \alpha \right | = n}A_{\alpha}\lambda_1^{\alpha_1}\lambda_2^{\alpha_2}\lambda_3^{\alpha_3} \ \ \ \ \ (6) Pn(λ1,λ2,λ3)=∣α∣=n∑Aαλ1α1λ2α2λ3α3 (6)
对于 L a g r a n g e Lagrange Lagrange 型形状函数,由于每个节点上只有一个自由度,所以 n n n 次形状函数有 T n T_n Tn 个节点与它对应。如果将 T n T_n Tn 个节点上的形状函数记为 ψ i ( Λ ) \psi_i(\Lambda) ψi(Λ),则
ψ i ( Λ j ) = δ i j = { 1 , i = j 0 , i ≠ j ( 7 ) \psi_i(\Lambda_j) = \delta_{ij} = \left\{\begin{matrix} 1, \ \ \ \ i = j \\ 0, \ \ \ i \neq j \\\end{matrix}\right. \ \ \ \ \ \ \ \ \ \ (7) ψi(Λj)=δij={1, i=j0, i=j (7)
其中 Λ j \Lambda_j Λj 为第 j j j点的面积坐标 ( λ 1 j , λ 2 j , λ 3 j ) (\lambda_{1j}, \lambda_{2j}, \lambda_{3j}) (λ1j,λ2j,λ3j)。由(7)的 T n T_n Tn个方程,可决定第 j j j 点相应的 n n n 次多项式的系数, 用此方法,在单元上可构成 T n T_n Tn 个 L a g r a n g e Lagrange Lagrange型的形状函数,而生成 ( T n , n , 0 ) (T_n, n, 0) (Tn,n,0)元素。
三角形单元上Lagrange型形状函数的节点坐标
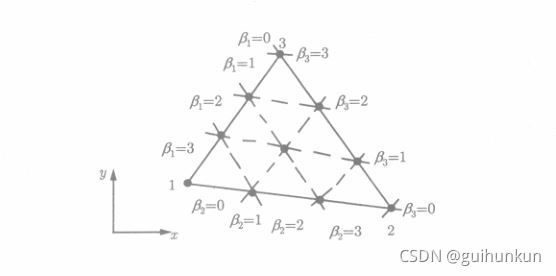
对于三角形的任意一条边,例如, 第一个顶点的对边 λ 1 = 0 \lambda_1 = 0 λ1=0,因此,在每一条边上的二元 n n n次多项式 P n P_n Pn变成一元 n n n次多项式,而由于它有 n + 1 n+1 n+1 个自由度,所以必须由该边上的 n + 1 n+1 n+1 个节点参数确定,这 n + 1 n+1 n+1 个节点取两个顶点和这边上的 n − 1 n-1 n−1个中间点。为简单,在 T n T_n Tn 个节点中,无论是 E n = 3 n E_n = 3n En=3n 个外节点,还是 T n − E n = ( n − 1 ) ( n − 2 ) / 2 T_n - E_n = (n-1)(n-2)/2 Tn−En=(n−1)(n−2)/2 个内节点,都均匀且对称地配置着,它们由下列直角坐标给出:
( ∑ l = 1 3 β l x l / n , ∑ l = 1 3 β l y l / n ) ( 8 ) (\sum_{l =1}^3 {\beta_l x_l/n}, \sum_{l =1}^3{\beta_ly_l/n}) \ \ \ \ \ \ \ \ \ (8) (l=1∑3βlxl/n,l=1∑3βlyl/n) (8)
其中 β = ( β 1 , β 2 , β 3 ) ∈ Z + 3 \beta = (\beta_1, \beta_2, \beta_3) \in Z_{+}^3 β=(β1,β2,β3)∈Z+3, 并满足
0 ≤ β l ≤ n , l = 1 , 2 , 3 ( 9 ) 0 \leq \beta_l \leq n, \ \ \ l = 1, 2, 3 \ \ \ \ \ \ \ \ \ (9) 0≤βl≤n, l=1,2,3 (9)
且不同的 ( β 1 , β 2 , β 3 ) (\beta_1, \beta_2, \beta_3) (β1,β2,β3) 对应不同的点。显然满足(9)的 β \beta β 恰恰有 T n T_n Tn个。将这样的 β \beta β的集合记为 B B B, 而 ( x l , y l ) ( l = 1 , 2 , 3 ) (x_l, y_l)(l = 1, 2, 3) (xl,yl)(l=1,2,3)是三角形三个顶点的直角坐标,则 T n T_n Tn 个节点的自然坐标即面积坐标 λ i ( i = 1 , 2 , 3 ) \lambda_i(i = 1, 2, 3) λi(i=1,2,3) 为
λ i σ = ∑ l = 1 3 β l λ i l / n , σ = 1 , 2 , . . . , T n ( 10 ) \lambda_{i\sigma} = \sum_{l = 1}^3{\beta_l \lambda_{il}/n}, \ \ \ \ \ \sigma = 1, 2, ..., T_n \ \ \ \ \ \ \ \ (10) λiσ=l=1∑3βlλil/n, σ=1,2,...,Tn (10)
由(8)可以推出,在 T n T_n Tn 个节点中一定包含三个顶点,其余的节点按平行与三条边连接成平行线,将原来的三角形分成 n 2 n^2 n2 个相等的三角形,这些小三角形的顶点作为单元的 T n T_n Tn 个节点, 如下图所示:
例如 n = 1 n = 1 n=1, 则 T n = 3 T_n = 3 Tn=3, 此时
B = { ( 1 , 0 , 0 ) , ( 0 , 1 , 0 ) , ( 0 , 0 , 1 ) } B = \{(1, 0, 0), (0, 1, 0), (0, 0, 1)\} B={(1,0,0),(0,1,0),(0,0,1)}
带入(10)得 3 个节点的面积坐标为
Λ 1 = ( λ 1 , λ 2 , λ 3 ) = ( 1 , 0 , 0 ) , Λ 2 = ( 0 , 1 , 0 ) , Λ 3 = ( 0 , 0 , 1 ) \Lambda_1 = (\lambda_1, \lambda_2, \lambda_3) = (1, 0, 0), \\ \Lambda_2 = (0, 1, 0), \ \ \ \ \ \ \Lambda_3 = (0, 0, 1) Λ1=(λ1,λ2,λ3)=(1,0,0),Λ2=(0,1,0), Λ3=(0,0,1)