关联规则及其Apriori算法实现（MATLAB）
前言
你是否有过这样的经历：在刷抖音的时候，总是容易刷到自己比较感兴趣的领域，比如说你喜欢玩游戏、看电影、看美女，那么你刷到的视频往往就在这几个之间徘徊；当你进入淘宝、京东想看点东西的时候，你想买的东西正好在搜索框的推荐项；当你QQ音乐的喜欢里有《稻香》，那么某一天你就会发现，推荐列表里就会出现《七里香》；你是否在疑惑，这些软件是怎么将我们的喜好联系起来的呢，这就运用到了关联规则。
`
一、关联规则的介绍
关联规则最初是为了解决购物篮问题而产生。购物篮分析(Market Basket Analysis)，20世纪90年代，大概是1993年，Agrawal等人第一次提出了关联规则的概念。到目前为止，我们最熟悉的故事就是啤酒和尿布的故事。
在一家超市里，有一个有趣的现象：尿布和啤酒赫然摆在一起出售。但是这个奇怪的举措却使尿布和啤酒的销量双双增加了。这不是一个笑话，而是发生在美国沃尔玛连锁店超市的真实案例，并一直为商家所津津乐道。
什么是关联规则？
关联规则：是形如X—>Y的蕴含表达式其中X和Y是不相交的项集，表示X与Y关联(可理解为：买了X后会买Y)
关联规则的衡量：支持度和置信度
支持度：规则出现的频率（概率）
置信度：X—>Y，确定Y在包含X事件中出现的频繁程度（条件概率）
如何挖掘关联规则？
关联规则挖掘过程主要包含两个阶段：
第一阶段必须先从资料集合中找出所有的高频项目组(Frequent Itemsets)，
第二阶段再由这些高频项目组中产生关联规则(Association Rules)。
如何找高频项目组，并找到项目之间的关联规则呢？
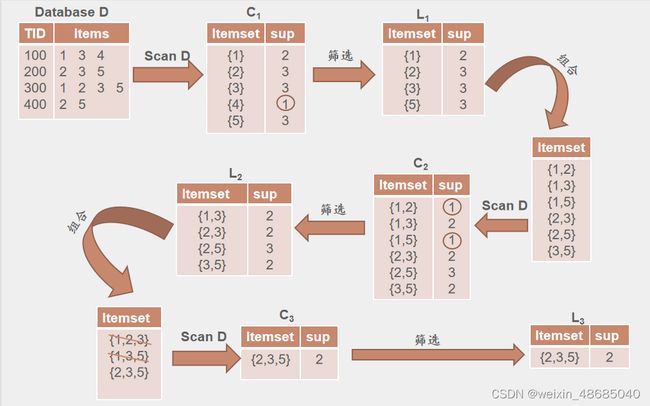
二、Apriori算法
基本思想
该算法的基本思想是：首先找出所有的频集，这些项集出现的频繁性至少和预定义的最小支持度一样。然后由频集产生强关联规则，这些规则必须满足最小支持度和最小可信度。然后使用第1步找到的频集产生期望的规则，产生只包含集合的项的所有规则，其中每一条规则的右部只有一项，这里采用的是中规则的定义。一旦这些规则被生成，那么只有那些大于用户给定的最小可信度的规则才被留下来。为了生成所有频集，使用了递推的方法。
基本原理
1.如果一个项集是频繁项集，那么它的子集（非空）就一定是频繁项集。
2.如果一个项集（非空）是非频繁项集，则其所有父集也是非频繁项集
算法流程
1.扫描数据集，从数据集中生成k项集Ck（k从1开始）；
2.计算Ck中，每个项集的支持度，删除低于阈值的项集，构成频繁项集Lk;
3.将频繁项集L中的元素进行组合，生成候选K+1项集C;
4.重复步骤2、3，直到满足以下两条件之一，算法结束。
（1） 频繁项集无法组合生成候选k+1项集
（2）所有候选k项集支持度都低于指定阈值（最小支持度），无法生成频繁k项集
由频繁项集生成关联规则
分别计算置信度，仅保留符合最小置信度的关联规则。
三、算法的实现（MATLAB）
main函数：
clear
%Apriori1: Items->C1->L1
%Apriori2: Lk->intemset(k)
%ST: 删除包含非频繁项目集子集的项目组
%Scan: intemset(k)->C(k+1)
%Apriori3: Ck->Lk
%第一步，找频繁k项集
T=[1 0 1 1 0
0 1 1 0 1
1 1 1 0 1
0 1 0 0 1];
RR=[]; %存储非频繁项目集
k=1; %项集数
supmin=0.5; %最小支持度
Min=supmin*4; %最小频数阈值
[L,R]=Apriori1(T,Min); %得到频繁1项集
fprintf('频繁%d项集为：\n',k);
disp(L);
RR=[RR;R];
k=k+1;
while true
A=Apriori2(L); %项目集
AA=ST(A,RR); %删除包含非频繁项目集的k项目集
C=Scan(T,AA,k);
fprintf('候选%d项集为：\n',k);
disp(C);
if isempty(C)
break;
end
[L,R]=Apriori3(C,Min);
fprintf('频繁%d项集为：\n',k);
disp(L);
if size(L,1)==1
break;
end
RR=[RR;R];
k=k+1;
end
[m,n]=size(L);
disp('可能产生关联的项目为:');
H=L(1,1:n-1)
%第二步，求符合最小置信度的关联规则
i=1;
t235=L(1,n); %记录频繁项集的频数
TT=sum(T); %将T的行累加
t2=TT(1,2); %各个项目的频数
t3=TT(1,3);
t5=TT(1,5);
t23=2; %多个项目同时存在的频数
t25=3;
t35=2;
fprintf('p2_35=%f\n',t235/t2)
fprintf('p3_25=%f\n',t235/t3)
fprintf('p5_23=%f\n',t235/t5)
fprintf('p23_5=%f\n',t235/t23)
fprintf('p25_3=%f\n',t235/t25)
fprintf('p35_2=%f\n',t235/t35)
Apriori1函数：
%由数据库得到频繁1项集,返回频繁项集和删除的项目集(Data->L1)
function [L,R]=Apriori1(T,supmin)
[~,n]=size(T); %事物集m，项目总数n
A=eye(n); %项目集用矩阵表示
B=(sum(T))'; %1项所有候选集的频数
i=1;
t=1;
while(i<=n)
if B(i,1)Apriori2函数：
%将频繁k项集转换成k+1项目集(Lk->itemset)
function AA=Apriori2(L)
k=2;
[m,n]=size(L);
A=L(:,1:n-1); %获取L的项目集
%k项目集组合成新的k+1项目集
t=1;
for i=1:m-1
for j=i+1:m
AA(t,:)=A(i,:)+A(j,:);
AA(AA~=0)=1; %当项目重复时，及时调整（1为有，0为无）
t=t+1;
end
end
%判断是否有重复的项目集,有就删除,行和大于k+1也删除
i=1;
s=sum(AA,2); %各行之和
while i<=size(AA,1)-1
j=i+1;
while j<=size(AA,1) %AA的行数
if AA(i,:)==AA(j,:) | s(i,1)>k+1 %行和大于k+1则删除
AA(i,:)=[];
s=sum(AA,2);
else
j=j+1;
end
end
i=i+1;
end
end
ST函数：
%删除项目集中包含非频繁项集的项目组（R为非频繁项集组成的矩阵）
function AA=ST(A,R)
i=1;
while i<=size(R,1)
j=1;
while j<=size(A,1)
if A(j,:)*R(i,:)'==sum(R(i,:)) %判断矩阵A的j行是否包含R的i行
A(j,:)=[];
else
j=j+1;
end
end
i=i+1;
end
AA=A;
end
Scan函数：
%扫描k项目集得到候选k项集
function C=Scan(T,A,k)
[a,~]=size(T); %矩阵T的行数
[m,~]=size(A); %矩阵A的行数
B=zeros(m,1); %创建m行n列的0矩阵
for i=1:a
for j=1:m
sum=T(i,:)*A(j,:)'; %将数据集的每行和k项目集的每行的转置相乘求和
if sum==k
B(j,1)=B(j,1)+1;
end
end
end
C=[A B];
end
Apriori3函数：
%将候选集k项集转换成频繁k项集（Ck->Lk)
function [L,R]=Apriori3(C,supmin)
[m,n]=size(C);
A=C(:,1:n-1); %C的项目集
B=C(:,n); %获取候选K项集每个项目集的频数
i=1;
R=[];
while(i<=m)
if C(i,n)
由此可以看出，{2,3—>5}和{3,5—>2}的关联规则较强，即买23就买5、买35就买2的可能性较高。