Avl树(有详细图解)
目录
介绍
引入
概念
特点
模拟实现
思路
插入
旋转
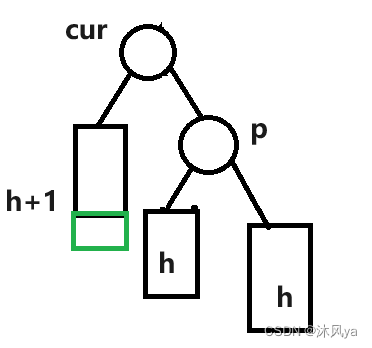
左旋
无子树
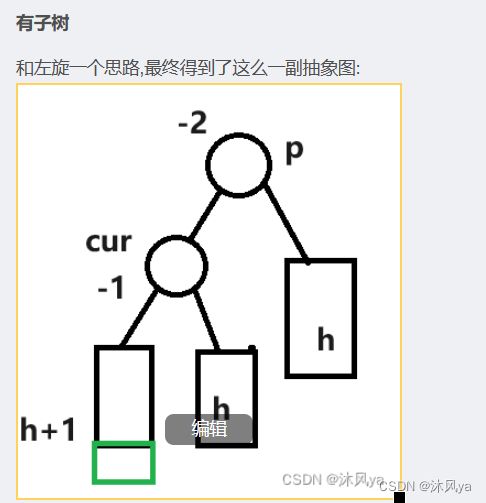
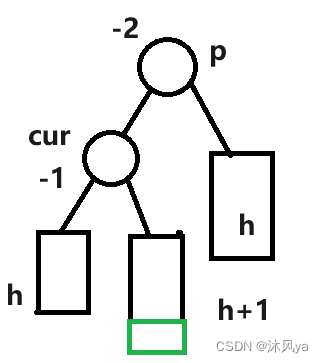
有子树
右旋
无子树
有子树
左右旋
引入(也就是有子树版本的抽象图解)
解决方法(也就是左右旋)
总结
无子树(也就是curright的位置就是newnode)
有子树
模型高度解释
旋转
更新三个节点的bf
右左旋
无子树
有子树
旋转
更新三个结点的bf
注意点
代码
介绍
引入
map和set的底层都是按照二叉搜索树来实现的
- 但是二叉搜索树有其自身的缺陷，假如往树中插入的元素有序或者接近有序，二叉搜索树就会退化成单支树，时间复杂度会退化成O(N)
- 因此map、set等关联式容器的底层结构是对二叉树进行了平衡处理，即采用平衡树来实现
概念
- AVL树是一种自平衡二叉搜索树，其名称源自其发明者Adelson-Velsky和Landis
- AVL树通过确保各个节点之间的高度差不超过1，来保证在最坏情况下，树的高度仍为O(log n) (其中n是树中节点的数量),这样可以保持最好的效率
特点
自平衡：在插入或删除节点时，AVL树会自动执行旋转操作来保持平衡。这些旋转操作包括左旋、右旋、左右旋和右左旋等，通过这些旋转可以调整节点的平衡因子，使其满足平衡条件(不超过1)
二叉搜索树性质：AVL树仍然是二叉搜索树，即左子树的所有节点的值都小于根节点的值，右子树的所有节点的值都大于根节点的值
模拟实现
思路
插入
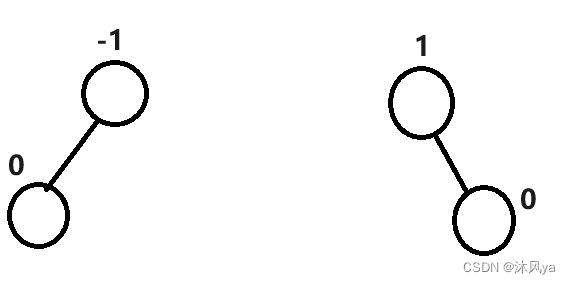
- avl树中保持平衡的关键就在于平衡因子(bf)
- 这里bf=右子树高度-左子树高度
- 主要就是每次插入时,需要更新平衡因子 (但只需要沿着newnode的位置往上就行,因为它改变的只是newnode所在那一分支)
- 只要当前结点bf=0,就可以不再更新了(它此时变为0,说明原来是1/-1)
- 那么让1/-1变为0,这一分支的高度是不变的,那么以这个为子树的树,高度也不会变,平衡因子也就不变
- 然后,如果结点bf=2/-2,就要开始旋转了
- 而旋转分为4种,需要判断cur和cur父亲的bf,来区分使用哪种旋转方式
- 而旋转后的子树,其根结点bf是0,那么他也是从在插入新结点前的1/-1变成了0,所以也就不需要往上更新了
- 这样,插入步骤就结束了
旋转
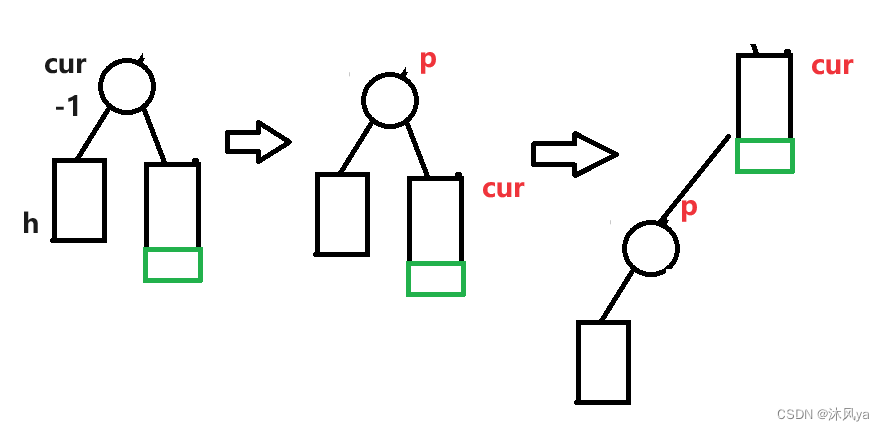
左旋
无子树
左旋实际上就是 -- 让p成为cur的左子树,cur的右边不受影响
有子树
- 虽然都有子树,但我们无法知道到底是多少个,到底是什么形态
- (这些其实我们都不关心,我们只要知道一个相对大小就行,毕竟重点还是在p和cur上)
- 有子树和无子树都是差不多的,只不过是多了子树,但是p和cur的bf仍然是2和1,只有这样才会触发左旋
- 然后设cur左子树高度为h,那么可以推出curright高度就是h+1,p左树是h
- 旋转后 -- cur的原左子树成为了p的右子树(因为本身curleft就处于p的右树范围),p左树不变,cur右树也不变
- 只要记住 -- 左旋是p成为cur的左树,那么原左树就成为了p的右树
- 旋转后的bf:(都为0)
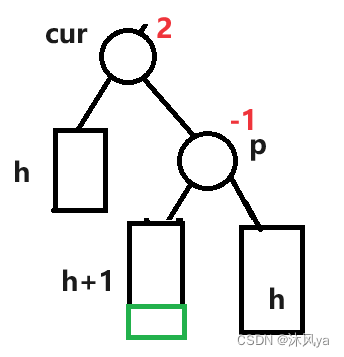
右旋
和左旋非常像,只不过是换了个方向
无子树
旋转后,p成为cur的右子树
有子树
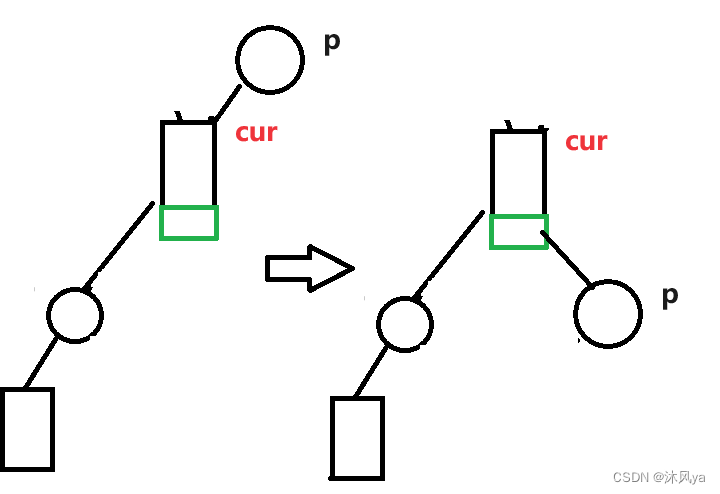
和左旋一个思路,最终得到了这么一副抽象图:
然后就是旋转了 -- cur原右子树成为p的左子树(本身就是p左树范围内),p右子树不变
计算bf后,两个结点的bf变成了0,其他的都不变
两种旋转真的非常像,只要记住左旋是p成为cur的左子树,右旋是p成为cur的右子树,就行了
左右旋
引入(也就是有子树版本的抽象图解)
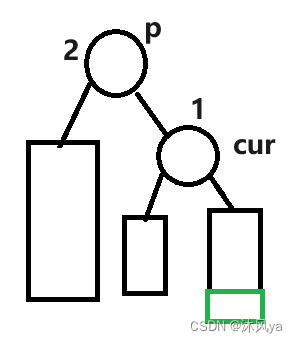
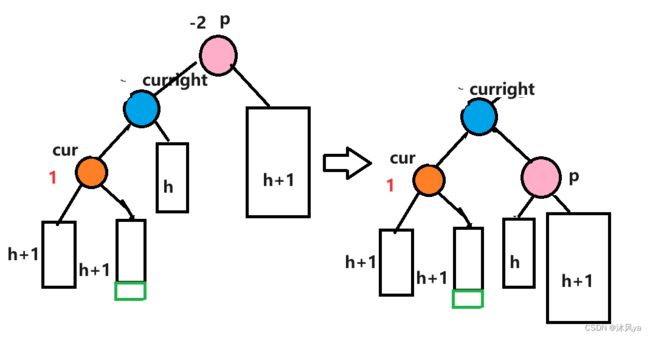
上面有这样一种情况,它是需要被右旋的:
但是如果这个新结点是在curright下呢???
这种情况不能使用单独的右旋(因为单右旋没有用):
会发现右旋后,这支子树的根结点的bf还是2(只是把原子树的左右颠倒了)
解决方法(也就是左右旋)
然后,我们经过对比可以发现,实际上他和右旋之间就差一个拐拐 :
所以可以考虑将那个拐角处掰正,也就是对应的将cur那支子树进行左旋:
这样,就可以和原来的p拼接起来,达到右旋的条件
最终经过右旋后,就可以完成我们的需求(这里只是抽象演示,并没有细画cur的情况,有子树中会有详细版)
总结
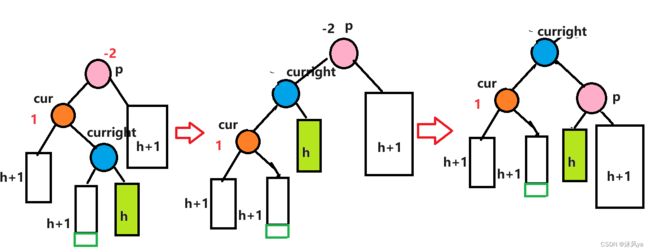
相当于对cur左旋是进行右旋的预热,最终其实还是经过对p右旋完成的
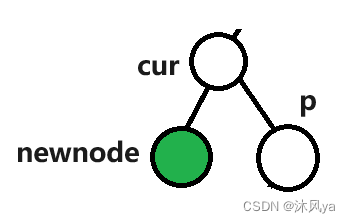
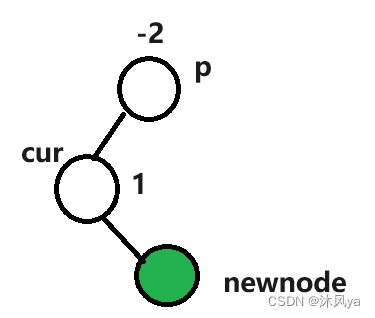
无子树(也就是curright的位置就是newnode)
先对cur进行左旋,然后对p右旋:
最终newnode(也就是curright成为了这一支子树的根结点)
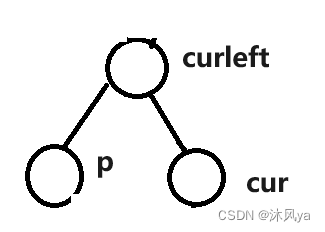
有子树
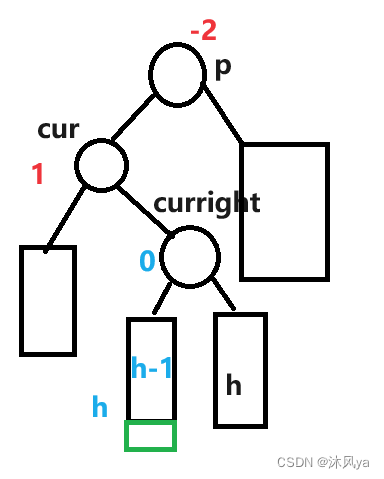
首先,在无子树情况中,我们会发现,最终cur的右结点成为了根,那么我们就需要额外画出这个结点
其次,新结点放在curright的左/右子树都可以,只不过最后处理这三个重要结点的bf时,需要单另处理
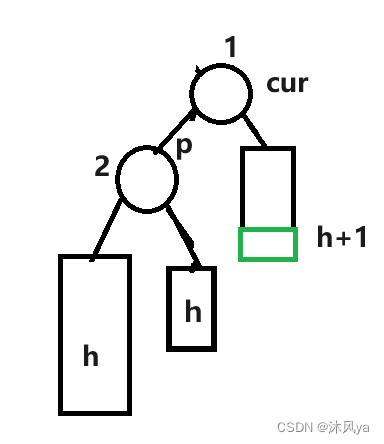
先抽象好模型(设curright右子树高度为h,从而可以推出其他高度)
模型高度解释
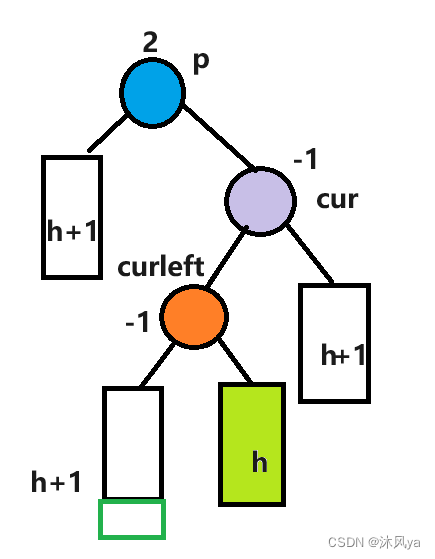
你可能会好奇,为什么curright的左右子树高度被写成是相等的? (至少我好奇了,然后我画了画,发现是有人家的理由的)
- 这里还是设右子树高度为h
- 如果原先左子树高度是h+1(高度差不能超过1嗷)
- 那新加一个结点就会变成h+2,会让curright的bf变成-2,那么这里不会触发p的左右旋,而是curright的旋转(左旋或者左右旋,具体看新结点的位置)
- 如果原先左子树高度是h-1(高度差不能超过1嗷)
- 那新加一个结点就会变成h,会让curright的bf变成0,那bf的更新到curright就停止了,不会让p更新到2/-2,所以依然不可以
那么就可以得到,curright的两个子树(如果有),那一定高度相等,才能触发p的左右旋
旋转
继续接下来的步骤,抽象好模型后,对cur进行左旋
不要忘记前面介绍的左旋了嗷(这里的cur成为curright的左子树,原左树成为cur的右子树)
然后和p连接在一起(也就是修改p的指向和两个结点的_parent指向)
接下来就是旋转的最后一步辣,对p进行右旋
这里是将p作为curright的右子树,原右子树成为p的左树(都是之前的步骤)
之后就是最重要的一步,对三个结点的bf重新赋值(虽然进行了旋转,但更新到的bf实际并不准确,因为右旋和左右旋用到的模型本身就不同)
更新三个节点的bf
这里的更新也得分情况
像这里用到的图解,是新结点插入在curright的左树部分
(下面是全部的旋转变换过程)
- 那么由于要对cur左旋的缘故,curright中带有新结点的这一支给了cur的右树,那么cur右边和左边平衡了,cur的bf=0
- 但p不一样,p的左树是被分配的curright的右树,其高度只有h(注意看图嗷看图),所以p的bf=1
如果新结点插入在curright的右树部分
- 道理和上面的一样
- 因为curright的右树给了p的左边:
- 所以p的bf=0(平衡了)
- 而cur的右边是原curright的左边,高度是0,所以cur的bf=-1
只要过程熟悉,知道是怎么变的,bf的更新也素手到擒来噜
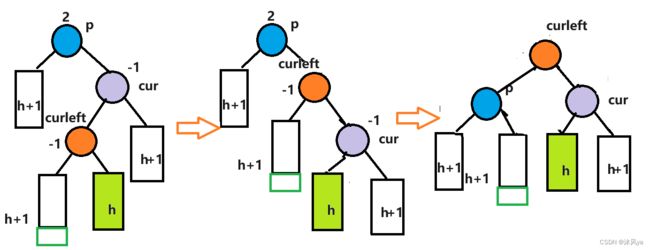
右左旋
和左右旋非常像,只不过是换了个方向
无子树
同样是有拐,也是一样要把那个拐掰正,也就是对cur进行右旋(让cur成为curleft的右子树)
最后就可以美美对p进行左旋噜
然后curleft成为了这一支的根结点
有子树
由于在左右旋中,我们已经分析了模型高度,所以我们直接画出右左旋的抽象模型(本质一样的)
旋转
接下来就是相似的操作,对curleft进行右旋
然后和p连接
就变成了标准的左旋状态,对p进行左旋:
最后就是:curleft的右结点通过右旋给了cur的左边,左结点经过左旋给了p的右边
更新三个结点的bf
这里用到的图解,是新结点插入在curleft的左树部分
像一直在重复说的那样(臣妾已经说倦了)
- 因为右旋,cueleft的右子树给了cur的左树,所以cur的左边是h,而右边是自己的h+1,所以cur的bf=1
- 因为左旋,curleft的左子树给了p的右子树,而右子树正是新结点插入位置,所以p的左边是h+1,右边是原先自己的h+1,相等了,所以p的bf=0
当新结点插入在curleft的右树部分
经过旋转后:
会发现:
- 新结点所在的右子树,在右旋中给了cur的左子树,所以cur的左右相等了,cur的bf=0
- 而给p的curleft右树高度仍是h,而p的左子树是自己的h+1,所以p的bf=-1
注意点
一定要写对插入的逻辑,还有 各种结点指向 / bf数值 的更新,超级重要!!!
- 亲身经历,本来以为对了,测试也是对的,过了几天加了点测试代码(因为实在是不好看这个代码到底写的对不对,又多又杂),结果就挂了
- 找了半天的错,发现旋转代码没问题,是我插入里面的"往上更新bf"逻辑错了
- 我是先一直更新到根结点,然后才找bf=2/-2的结点
- 就导致,旋转完后子树的bf是对的,它父结点的bf错了,本来就不应该更新它的!(我哭死)
然后就是旋转里面,"原子树根结点的父结点"的指向要注意不要漏掉,要更新啊!!!
其他的好像就没啥了,只要多多写备注,就应该没啥问题
代码
#include
#include
#include
#include
#include
#include
namespace my_AvlTree
{
template
struct AvlTreeNode
{
AvlTreeNode(const T &data = T())
: _left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _bf(0)
{
}
AvlTreeNode *_left;
AvlTreeNode *_right;
AvlTreeNode *_parent;
T _data;
int _bf; // 节点的平衡因子
};
// AVL: 二叉搜索树 + 平衡因子的限制
template
class AvlTree
{
typedef AvlTreeNode Node;
public:
AvlTree()
: _root(nullptr)
{
}
// 在AVL树中插入值为data的节点
bool Insert(const T &data);
// AVL树的验证
bool IsAvlTree()
{
return _IsAvlTree(_root);
}
void levelOrder();
size_t Height()
{
return _Height(_root);
}
private:
// 根据AVL树的概念验证pRoot是否为有效的AVL树
bool _IsAvlTree(Node *root);
size_t _Height(Node *root);
// 右单旋
void RotateR(Node *parent);
// 左单旋
void RotateL(Node *parent);
// 右左双旋
void RotateRL(Node *parent);
// 左右双旋
void RotateLR(Node *parent);
private:
Node *_root;
};
template
void AvlTree::levelOrder()
{
Node *root = _root;
std::vector> arr;
std::queue q;
if (root != nullptr)
{
q.push(root);
}
while (!q.empty())
{
std::vector tmp; // 存储一层的结点
int size = q.size(); // 此时队列内的元素就是上一层的结点个数
for (int i = 0; i < size; ++i)
{
tmp.push_back(q.front()->_data);
if (q.front()->_left)
{ // 有子树就放进队列中
q.push(q.front()->_left);
}
if (q.front()->_right)
{
q.push(q.front()->_right);
}
q.pop(); // 出掉这个父结点
}
arr.push_back(tmp);
}
for (auto &i : arr)
{
for (auto &j : i)
{
std::cout << j << " ";
}
std::cout << std::endl;
}
}
template
bool AvlTree::Insert(const T &data)
{
if (_root == nullptr)
{
_root = new Node(data);
}
else
{
Node *cur = _root, *parent = cur, *newnode = nullptr;
// 找到插入位置
while (cur)
{
if (data > cur->_data)
{
parent = cur;
cur = cur->_right;
}
else if (data < cur->_data)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
// 插入+改父亲bf
newnode = new Node(data);
if (data < parent->_data)
{
parent->_left = newnode;
--parent->_bf;
newnode->_parent = parent;
}
else
{
parent->_right = newnode;
++parent->_bf;
newnode->_parent = parent;
}
// std::cout << "parent:" << parent->_data << " "
// << "newnode:" << newnode->_data << std::endl;
// 维护bf
cur = parent; //注意,这里不能直接定义cur的父结点,因为不能保证cur不为空(如果此时只有俩结点,就为空了!!!)
while (cur != _root)
{
Node *pnode = cur->_parent;
// 更新bf
if (pnode->_left == cur)
{
--pnode->_bf;
}
else
{
++pnode->_bf;
}
// 判断是否继续往上更新
if (cur->_bf == 0)
{
break;
}
else
{
if (pnode->_bf == 2 || pnode->_bf == -2)
{
// pnode就是不合法的结点,然后判断它该怎么调整
if (pnode->_bf == -2 && cur->_bf == -1)
{
// 右单旋
RotateR(pnode);
}
if (pnode->_bf == 2 && cur->_bf == 1)
{
// 左单旋
RotateL(pnode);
}
if (pnode->_bf == -2 && cur->_bf == 1)
{
// 左右双旋
RotateLR(pnode);
}
if (pnode->_bf == 2 && cur->_bf == -1)
{
// 右左双旋
RotateRL(pnode);
}
break;
}
else
{
cur = pnode;
pnode = pnode->_parent;
}
}
}
}
return true;
}
template
bool AvlTree::_IsAvlTree(Node *root)
{
if (root == nullptr)
{
return true;
}
int left_height = _Height(root->_left);
int right_height = _Height(root->_right);
if (right_height - left_height != root->_bf) //不要太相信自己写的bf计算方法
{
std::cout << right_height << std::endl;
std::cout << left_height << std::endl;
std::cout << root->_bf << std::endl;
std::cout << "平衡因子异常" << std::endl;
return false;
}
return abs(right_height - left_height) < 2 && _IsAvlTree(root->_left) && _IsAvlTree(root->_right);
}
template
size_t AvlTree::_Height(Node *root)
{
if (root == nullptr)
{
return 0;
}
int leftsize = _Height(root->_left) + 1;
int rightsize = _Height(root->_right) + 1;
return leftsize > rightsize ? leftsize : rightsize;
}
template
void AvlTree::RotateL(Node *parent)
{
Node *cur = parent->_right, *curleft = cur->_left, *ppnode = parent->_parent;
// 连接cur上需要修改的子树(比如左旋就是让parent当cur的左子树,那么cur左树就得和parent右边相连)
if (curleft) // 防止左树为空
{
curleft->_parent = parent;
}
parent->_right = curleft;
// 连接cur和parent
cur->_left = parent;
// 修改parent父结点的指向
if (ppnode == nullptr) // 如果此时parent是根结点,那么它没有父结点,且需要更新根结点
{
_root = cur;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = cur;
}
else
{
ppnode->_right = cur;
}
}
// 改父结点指向(千万别忘辣!!!)
cur->_parent = ppnode;
parent->_parent = cur;
// 维护bf
cur->_bf = parent->_bf = 0;
}
template
void AvlTree::RotateR(Node *parent)
{
Node *cur = parent->_left, *curright = cur->_right, *ppnode = parent->_parent;
// 连接cur上需要修改的子树(右旋就是让parent当cur的右子树,那么cur右树就得和parent左边相连)
if (curright) // 防止右树为空
{
curright->_parent = parent;
}
parent->_left = curright;
// 连接cur和parent
cur->_right = parent;
// 修改parent父结点的指向
if (ppnode == nullptr) // 如果此时parent是根结点,那么它没有父结点,且需要更新根结点
{
_root = cur;
}
else
{
if (ppnode->_left == parent)
{
ppnode->_left = cur;
}
else
{
ppnode->_right = cur;
}
}
// 改父结点指向
cur->_parent = ppnode;
parent->_parent = cur;
// 维护bf
cur->_bf = parent->_bf = 0;
}
template
void AvlTree::RotateLR(Node *parent)
{
Node *cur = parent->_left, *curright = cur->_right;
int bf_comp = curright->_bf; // 用于判断插入结点的左右位置
RotateL(parent->_left); // 让cur成为curright的左子树
RotateR(parent); // 让parent成为curright的右子树
// curright是旋转后子树的根结点
// 最终让curright的左子树给了cur的右子树,curright的右子树给了parent的左子树
// if (_Height(curright) == 1)
// {
// curright->_bf = 0;
// cur->_bf = 0;
// parent->_bf = 0;
// }
if (bf_comp == 0)
{
curright->_bf = 0;
cur->_bf = 0;
parent->_bf = 0;
}
else
{
if (bf_comp == -1) // 在curright的左边
{
// 说明cur的右子树多了1,使其与原先的左子树高度相等
// 而parent的左子树是h-1,右子树是原先的h
curright->_bf = 0;
cur->_bf = 0;
parent->_bf = 1;
}
else if (bf_comp == 1) // 在curright的右边
{
// 说明parent的左子树多了1,使其与原先的右子树高度相等
// 而cur的右子树是h-1,左子树是原先的h
curright->_bf = 0;
cur->_bf = -1;
parent->_bf = 0;
}
else
{
assert(false);
}
}
}
template
void AvlTree::RotateRL(Node *parent) // 插入结点在curleft的左右子树上其中一个位置
{
Node *cur = parent->_right, *curleft = cur->_left;
int bf_comp = curleft->_bf; // 用于判断插入结点的左右位置
RotateR(parent->_right); // 让cur成为curleft的右子树
RotateL(parent); // 让parent成为curleft的左子树
// curleft是旋转后子树的根结点
// 最终让原curleft的右子树给了cur的左子树,curleft的左子树给了parent的右子树
// if (_Height(curleft) == 1)
// {
// curleft->_bf = 0;
// cur->_bf = 0;
// parent->_bf = 0;
// }
if (bf_comp == 0)
{
curleft->_bf = 0;
cur->_bf = 0;
parent->_bf = 0;
}
else
{
if (bf_comp == -1) // 在curleft的左边
{
// 说明parent右子树多了1,使其与原先的左子树高度相等
// 而cur的左子树是h-1,右子树是原先的h
curleft->_bf = 0;
cur->_bf = 1;
parent->_bf = 0;
}
if (bf_comp == 1) // 在curleft的右边
{
// 说明cur的左子树多了1,使其与原先的右子树高度相等
// 而parent的右子树是h-1,左子树是原先的h
curleft->_bf = 0;
cur->_bf = 0;
parent->_bf = -1;
}
}
}
}