一起学数据结构（7）——树及二叉树的基本概念及存储

前面的关于数据结构的文章中，介绍了顺序表，链表，栈，队列等数据结构。对于以上数据结构，均是一对一的关系。本篇文章将对于一对多的数据结构——树进行解析。

目录

1. 树的定义及基本概念：

1.1 树的定义：

1.2 树的基本概念及术语：

2. 树的存储：

3. 二叉树的概念及结构 ：

3.1 二叉树的概念：

3.2 两种特殊的二叉树：

3.2.1 满二叉树：

3.2.2 完全二叉树：

3.3 二叉树的存储：

3.3.1 完全二叉树的存储：

3.3.2堆的相关概念：

3.3.3 非完全二叉树的存储：

---

1. 树的定义及基本概念：

1.1 树的定义：

树是个结点的有限集，当时，把树称之为空树。对于任意的非空树，应该满足下面的条件：

1. 有且仅有一个特定的根结点

2.当时，除根结点之外的其他结点可以再分为个互不相交的有限集,并且每个有限集本身也可以看作一棵树，并且称之为根的子树。

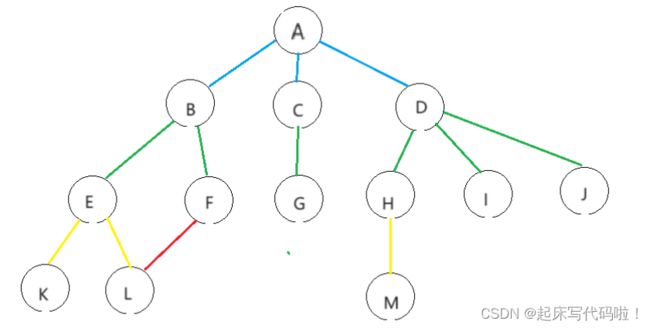
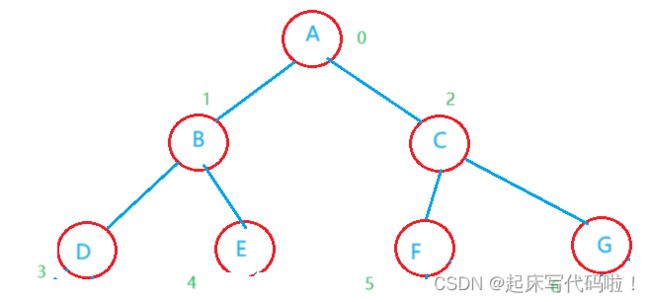
树的结构可以由下图表示：

从给出的树的结构图可以看出，树的定义是满足递归的，即：树在定义的过程中，多次用到了自身。所以，树是一种递归的数据结构，同时，满足下面的两个特点：

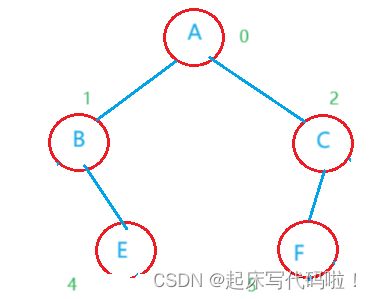
(1).根结点没有前驱，除根结点以外的结点有且仅有一个前驱。如果对上述树的结构图进行更改：

本图中结点因为由两个前驱，即结点。所以，上图不满足树的结构，不为树。

(2).树中所有结点都可以又零个或者多个后继结点。 

1.2 树的基本概念及术语：

(1).结点的度：一个结点含有子树的个数，被称之为该结点的度，图中，结点的度为。

(2).叶结点或终端结点：度为的结点称之为叶结点，图中均为叶结点。

(3).非终端结点或分支结点：度不为的结点为分支结点。图中均为分支结点。

(4).双亲结点或者父结点：若一个结点含有一个子结点，则这个结点称为子结点的父结点。

(5).子结点：一个结点含有的子树的根结点，称之为该结点的子结点，图中均为结点的子结点。

(6).兄弟结点：具有相同父结点的结点，称之为兄弟结点。

(7).树的度：树中最大的结点的度，称之为树的度。图中树的度为.

(8).结点的层次：从根结点开始定义，根结点为第层，以此类推。

(9).树的高度：树中最大的结点的层次，图中树的高度为。

(10).堂兄弟结点：父结点在同一层的结点，称之为堂兄弟结点，图中就互为堂兄弟结点。

(11).结点的祖先：从根到该结点所经分支的所有结点。例如，图中的祖先结点为。

(12).子孙结点：以某结点为根的子树中任一结点都为该结点的子孙结点。

(13).森林：由棵互不相交的树构成的集合称之为森林。

2. 树的存储：

在存储上述给出的树时，由于每一个结点下面的子结点的数量都是随机的，所以，只有在得知结点的度的情况下，才可以提前开辟一定量的空间进行存储。但是在大多数情况下，结点的度都是未知的，对于上述情况，采取的存储方式为左孩子，右兄弟的存储方法，具体结构如下：

struct TreeNode
{
     int val;
     struct TreeNode* firstchild;
     struct TreeNode* nextbrother;
};

其中，用于存储数据元素，结构体指针用于指向该结点最靠左部分的子结点，用于指向子结点的兄弟结点。

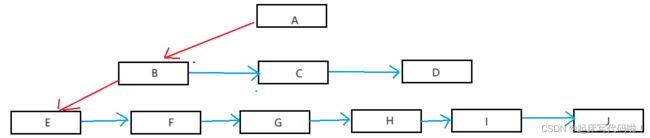
若用上面的存储方法来表示给出的树的结构，其中红线表示结构体指针的指向，蓝线表示结构体指针的指向，效果图如下：

对于由棵互不相交的树构成的森林，也可以采用双亲表示法进行存储，原理如下：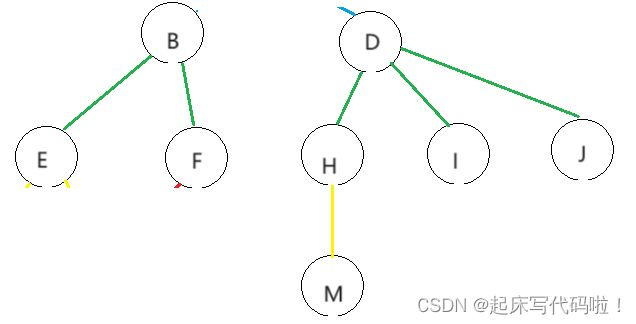

在采用双亲表示法对上述的森林进行存储时，需要创建一定大小的数组，用于存放若干个结构体，每个结构体均是森林中子树的结点，即：

在上一个存储方法中，分别存储了子结点和兄弟结点的地址。对于双亲表示法，则是存储该结点父结点的指针或者下标。 例如上面给出的数组，若该结点不存在父结点，则直接存储，若存在父结点，需要存储父结点的下标，效果如下：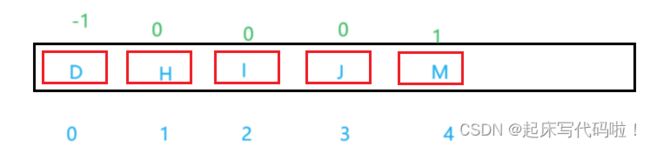

其中，绿色数字代表该结点的父结点的下标。

从上面对于树的简单介绍可以看出，相对于之前的顺序表，链表等数据结构来说，树的结构较为复杂。但是，在实际使用时，只有二叉树这一种特殊的结构比较泛用，下面将对于二叉树的内容进行介绍。

3. 二叉树的概念及结构 ：

3.1 二叉树的概念：

二叉树是一种特殊的数据结构，特点是每个结点至多只有两棵子树，即：二叉树中不存在度大于的结点。并且二叉树有左右之分，且顺序不可以颠倒。

与树相同，二叉树也是由个结点构成的有限集合。当时，此时的二叉树被称之为空树。当时，此时二叉树只有一个根节点。当时，此时的二叉树有左树、右树两种形式。当是，此时的二叉树有左、右两棵子树。即：

对的任意二叉树，均可以看作由上述情况复合而来。

3.2 两种特殊的二叉树：

3.2.1 满二叉树：

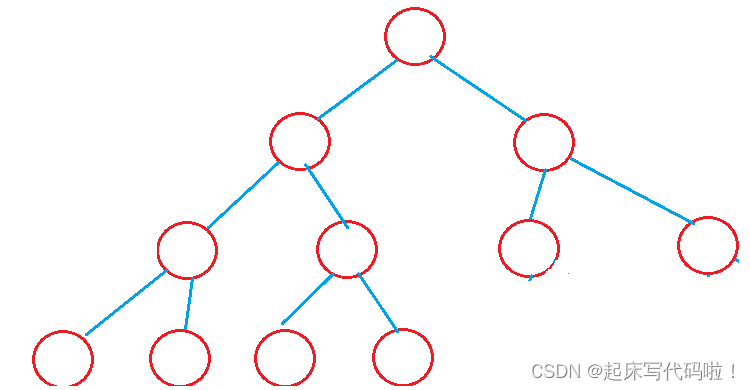
对于一个二叉树，如果每一层的结点数都到达了最大值，则称这个二叉树为满二叉树，满二叉树结构如下：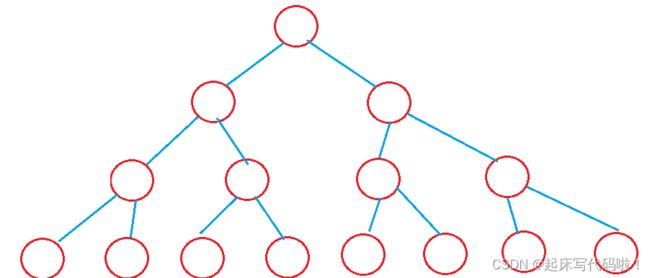

对于一个高度为的满二叉树，由于每一层的结点都达到了最大值，满二叉树中的结点总数为

3.2.2 完全二叉树：

对于完全二叉树，是一种效率很高的数据结构，完全二叉树是由满二叉树引出来的。对于一个高度为,有个结点的二叉树，当且仅当每一个结点都与高度为的满二叉树编号从到的结点一一对应时，称之为完全二叉树。对于满二叉树，可以看作成一种特殊的完全二叉树。也可以理解为，一个高度为的完全二叉树，其前层的结点数都达到了最大值。但是在第层，结点的数量可以小于最大值，但是结点的排列必须是连续的，即下图中所展示的结构。：

而对于下面这种结点排列不连续的二叉树，则不可以看作完全二叉树：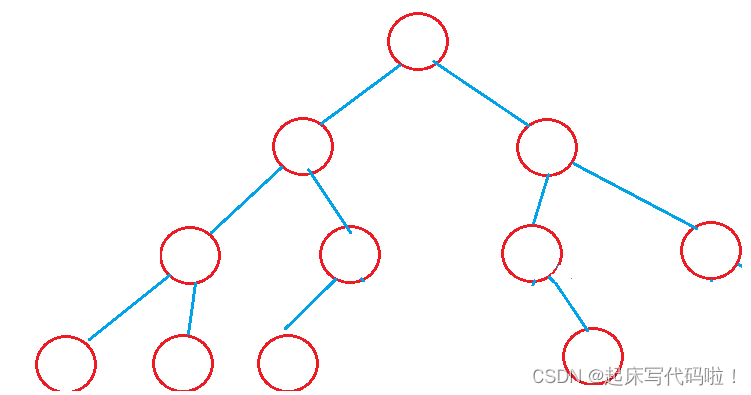

前面说到，满二叉树可以看作一个特殊的完全二叉树。故，一个完全二叉树的结点数量的最大值为。通过上述给出的完全二叉树的结构，可以的出，当完全二叉树结点数量的最小值，就是第层只有一个结点，结构如下：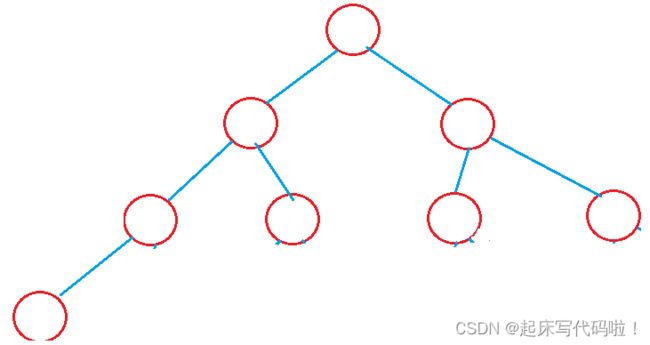

此时的完全二叉树的结点数量为.所以，完全二叉树的结点数量的范围为:                  

                                                            

3.3 二叉树的存储：

3.3.1 完全二叉树的存储：

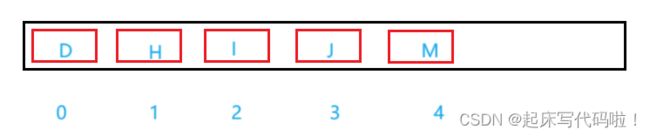
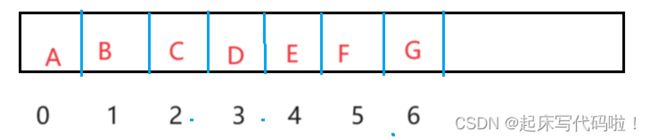
对于一个完全二叉树，在进行存储时，可以采用顺序存储的方式进行存储，例如对于下列完全二叉树：

其顺序存储方式可以表示为：

通过数组的下标，可以总结出下面的等式：

对于每个父结点，其左子结点的下标为。其右子结点的下标为：。对于每个子结点，其父结点的下标可以表示为：，左、右子结点均通用。

3.3.2堆的相关概念：

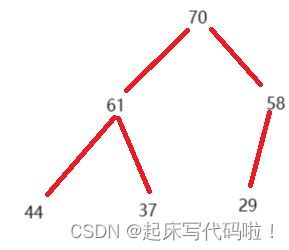
对于完全二叉树的顺序存储，一个比较典型的例子就是堆：堆是一个非线性结构的数据结构，结构上满足完全二叉树，适合用顺序存储。堆可以分为两种：

(1).小堆：树中任何一个父节点存储的值都子结点存储的值。

顺序存储可以表示为：

(2).大堆：树中任何一个父结点存储的值都子结点存储的值。例如：

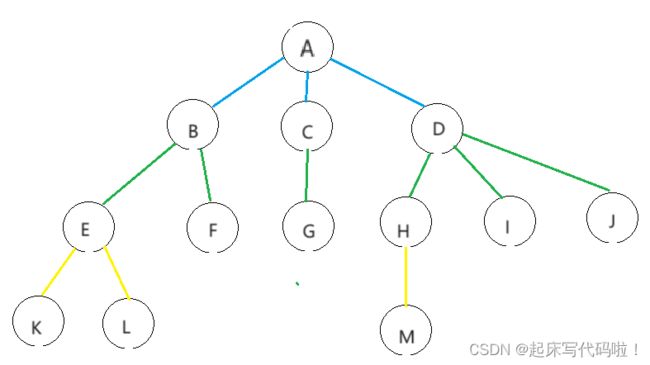
3.3.3 非完全二叉树的存储：

将上面给出的完全二叉树删除其中的几个结点，改造成非完全二叉树。如果用顺序存储方式来存储非完全二叉树，则其顺序存储方式可以表示为：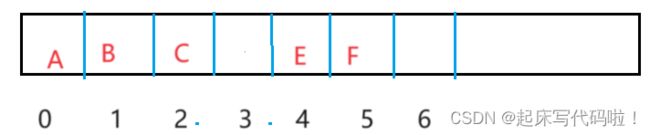

 

对应非完全二叉树的结构为：

对于给出的非二叉树，将不再适用于上面给出的两个等式。这是因为，当在计算机中建立上述非完全二叉树时，二叉树的结构与图中表示不同，而是把看作的一个子结点，而非的子结点。也就是说，的下标应该是，的坐标为，与顺序表示方法中的下标编号不同。故不能采用顺序存储。

对于非完全二叉树的存储，一般采用链式存储。