算法通过村第九关-二分(中序遍历)白银笔记|二分搜索

---

前言

---

提示：我不想再听人说什么了，我想听听松树和风说了什么。 --巴呀呀《因思念而沉着》

二分查找很经典，但是面试的时候一般不直接考察这个问题，而是考察其变形题目，我们看下。

另外，二分查找和二叉搜索树有异曲同工之妙，具体我们就向下看吧。

基于二分查找思想，可以扩展除很多算法问题，而且很多都是考察热门问题，这里我们找些经典问题看看

二分查找在算法中应用也非常多，也是很多大厂所钟爱的考察类型，感兴趣的同学可以进一步学习研究一下：

推荐下面这些题目⭐⭐⭐⭐⭐：

LCR 172. 统计目标成绩的出现次数 - 力扣（LeetCode）

LCR 173. 点名 - 力扣（LeetCode）

34. 在排序数组中查找元素的第一个和最后一个位置 - 力扣（LeetCode）

875. 爱吃香蕉的珂珂 - 力扣（LeetCode）

29. 两数相除 - 力扣（LeetCode）

在前面我们发现很多题目使用前序，后序或者层次遍历都可以解决，但是几乎没有中序遍历的。这是因为中序和前序后序的特点不一样，例如中序可以和搜索树结合在一起，前序和后序就不可以。

理解了二分搜索树之后，你会发现一个惊天密码，二分中序竟然是一个问题，真的像，这里我们就学习一下。

1. 基于二分查找的拓展问题

1.1 山脉数组的峰顶索引

参考题目介绍：852. 山脉数组的峰顶索引 - 力扣（LeetCode）

看着这个题目要求有点多，核心就是一个，在数组中找到每个位置开始i，从0到i是递增的，从i+ 1之后就是递减的的，找到这个i的位置就是结果了。

所以根据这个问题，和前面的找最小值相关的过程一样。最简单的方式就是对数组遍历一次，当我们遍历到的下标满足：arr[i - 1] < arr[i] > arr[i + 1]，那么此时i就是我们要的结果。

其实也可以再简单一些，因为是从左开始找，那开始时必然满足arr[i - 1] < arr[i],所以我们只要找到第一个满足arr[i] > arr[i + 1]的位置就可以了。

	/**
     * 一次遍历 i= 1
     * @param arr
     * @return
     */
    public static int peakIndexInMountainArray(int[] arr) {
       int n = arr.length;
       int res = -1;
       // 从1 开始就神
       for(int i = 1; i < n - 1; i++){
           if (arr[i] > arr[i+1]){
               res = i;
               break;
           }
       }
       return res;
    }

这个题可以采用二分的思想吗？ 当然可以

对于二分的某个位置mid，mid可能有3种情况：

• mid在上升阶段，满足arr[mid] > arr[mid - 1] && arr[mid] < arr[mid + 1];
• mid在顶峰阶段，满足arr[mid] > arr[mid - 1] && arr[mid] > arr[mid + 1]
• mid在下降阶段。满足arr[mid] < arr[mid - 1] && arr[mid] > arr[mid + 1]

因此我们根据mid当前所在的位置，调整二分的左右指针，就可以很快的找到顶峰。

代码如下：

    /**
     * 二分查找  捉拿边界问题
     * @param arr
     * @return
     */
	public int peakIndexInMountainArray(int[] arr) {
        if (arr.length == 3){
            return 1;
        }
        // 二分的左右指针 边界
        int left = 1, right = arr.length - 2;
        while(left <= right){
            int mid = left + ((right - left) >> 1);
            if (arr[mid] > arr[mid - 1] && arr[mid] > arr[mid + 1]){
                return mid;
            }
            if (arr[mid] < arr[mid - 1] && arr[mid] > arr[mid + 1]){
                // 下降阶段
                right = mid - 1;
            }
            if (arr[mid] > arr[mid - 1] && arr[mid] < arr[mid + 1]){
                // 上升降阶段
                left = mid + 1;
            }
        }
        return left;
    }

1.2 旋转数字的最小数字

参考题目介绍：153. 寻找旋转排序数组中的最小值 - 力扣（LeetCode）

读了这个题，你有没有和我一样不知道题目是说什么的？我们看看力扣的官方的图解吧：

其中横轴表示数组元素的下标，纵轴表示数组元素的值。途中编出了最小值的位置，是需要我们查找的目标值。

我们考虑数组中的最后一个元素x：在最小值右侧的元素（不包括最后一个元素本身）它的值一定是严格小于x；

而在最小值左侧的元素，它的值一定是严格大于x。因此我们可以根据这个特性，通过二分的方法找出最小值。

在二分查找的第一步，判断边界：

low 左边界 high 有边界 区间中点 pivot 也就是最小值在该区间内

我们将中轴元素nums[pivot]与右边界元素nums[high]进行比较，有可能存在一下三种情况：

• 第一种情况：nums[pivot] < nums[high]。如下图所示，说明nums[privot]是最小值右侧的元素，因此我们可以忽略二分查找区间的右半部分。

• 第二种情况：nums[pivot] > nums[high]。如下图所示，这个说明nums[pivot]是最小值的左侧元素，因此可以忽略二分查找区间的左半部分。

• 第三种情况： 由于数组不包含重复元素，并且只要当前的区间长度不为1，pivot就不会与high重合，而如果当前的区间长度为1，这说明我我们已经可以结束二分查找二零。因此不会存在nums[pivot] == nums[hight]的情况

当二分结束的时候，我们就可以得到最小值所在的位置了。

	/**
     * 旋转数字的最小数字
     * @param nums
     * @return
     */
    public static int findMin(int[] nums) {
        int low = 0;
        int high = nums.length - 1;
        while(low < high) {
            int pivot = low + ((high - low) >> 1);
            // 注意这里的变化
            if (nums[pivot] < nums[high]){
                high = pivot;
            }else {
                low = pivot + 1;
            }
        }
        return nums[low];
    }

这里你是否注意到high = pivot；而不是我们习惯上的high = pivot - 1 呢？ 这里为了防止遗漏元素，例如[3,1,2]，执行的时候nums[pivot] = 1，小于nums[high] = 2，此时如果high = pivot - 1，这里直接会变成0。所以对于边界问题情况，很难去解释清楚，最好的策略就是多写几种场景测试一下看看。这也是二分查找比较烦的情况，一般来说解释起来比较困难，也不容易理解清楚，所以写几个经典的例子试一下，面试的时候大部分case能过就能通过。

我们这里也可以拓展一下，如果在上面的基础上存在重复元素会怎么样呢？感兴趣的同学可以研究一下这个题。

推荐题目⭐⭐⭐⭐：

154. 寻找旋转排序数组中的最小值 II - 力扣（LeetCode）

1.3 寻找缺失数字

参考地址：剑指offer面试题53题目二-0-n-1中缺失的数字_剑指offer 缺失的数字_执子手 吹散苍茫茫烟波的博客-CSDN博客

这道题很简单吧？说实话从头到尾遍历一边不久解决了吗？但是这么简单肯定不是面试需要的。这里要考察的点是什么呢？就是二分查找！！

对于有序的也是可以采用二分查找，这里的关键点是在缺失的数字之前，必然有nums[i] = i，在缺失的数字之后，必然有nums[i] != i.

因此，只需要二分找出第一个nums[i] != i，此时下标i就是答案了。如果数组中没有找到次下标，那么缺失的就是n。

考虑下怎么写的？代码很简单：

	 /**
     * 寻找缺失数
     * @param nums
     * @return
     */
    public static int solve(int[] nums) {
       int left = 0;
       int right = nums.length - 1;
       while(left <= right ){
           int mid = left + ((right - left) >> 1);
           if (nums[mid] == mid){
               left = mid + 1;
           }else{
               right = mid - 1;
           }
       }
        return left;
    }

1.4 优化求平方根

参考题目介绍：69. x 的平方根 - 力扣（LeetCode）

这个其实很简单，需要注意的地方要考虑下。

/**
 * 二叉求平方根
 * @param x
 * @return
 */
public static int sqrt (int x) {
  int left = 1;
  int right = x;
  int res = -1;
  while(left <= right){
      // 注意写法
      int mid = left + ((right - left)>>1);
      // 这个小技巧留一下
      if(x / mid >= mid ){
          res = mid;
          // 返回多加1
          left = mid + 1;
      }else if (x / mid < mid){
          right = mid - 1;
      }
  }
  return res;
}

记住这种优化的思想，凡是在有序的区间内查找的场景，都可以用二分查找来优化速度。如果有序区间是变化的，那么每次都要针对这个变化区间进行二分。这种问题做多了可以体会一下。

2. 中序与搜索树原理

在前面我们看了很多前序、后序或者层次遍历解决的问题，很少遇到有中序遍历解决的。这是因为中序与前后序相比较有不一样的特征，例如中序可以和搜索树结合在一起，但是前序和后序就不行了。

二叉搜索树是一个很简单的概念，但是想说清楚也不容易。简单来说就是如果一棵二叉树就是搜索树，按照中序遍历其序列正好是一个递增序列。比较规范的定义是：

• 若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值。
• 若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值。
• 它的左右子树也分别是二叉排序树。

下面是一个中序序列{3，6，9，10，14，16，19}，一个{3，6，9，10}，都是搜索树。

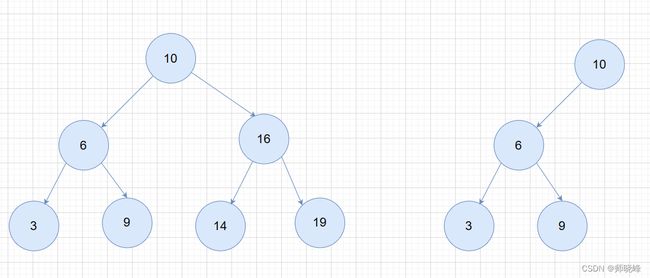
搜索树的题目虽然依然是递归，但是与前后遍历区别很大，主要是因为搜索树是有序的，就是可以根据条件决定某些递归就不必执行了，也就是所谓的“剪枝”。

2.1 二叉搜索树中搜索特定值

参考题目介绍：700. 二叉搜索树中的搜索 - 力扣（LeetCode）

这道题看起来挺复杂的，但是实现起来却很简单，简单递归搞定：

• 如果根节点为空 root == null 或者根节点的值等于搜索值 val == root.val，返回根节点。
• 如果val < root.val ，进入到根节点的左子树 查找searchBST(root.left, val)。
• 如果val > root.val ，进入到根节点的右子树 查找searchBST(root.right, val)。

递归写法：

    /**
     * 递归方式实现
     *
     * @param root
     * @param val
     * @return
     */
public static TreeNode searchBST(TreeNode root, int val) {
    // 校验参数
    if(root == null || root.val == val) {
        return  root;
    }
    return root.val > val ? searchBST(root.left,val) : searchBST(root.right,val);
}

迭代写法：

• 条件：根节点不空 root != null 且 根节点不是目标节点值 val != root.val

  • 如果val < root.val ，进入到根节点的左子树 查找root = root.left
  • 如果val > root.val ，进入到根节点的右子树 查找root = root.right

    /**
     * 迭代实现
     *
     * @param root
     * @param val
     * @return
     */
    public static TreeNode searchBST2(TreeNode root, int val) {
       while(root != null && root.val != val){
          root = root.val > val ? root.left : root.right;
       }
       return root;
    }

2.2 验证二叉搜索树

参考题目介绍：98. 验证二叉搜索树 - 力扣（LeetCode）

根据这个题目给出的性质，我们可以进一步直到二叉树【中序遍历】得到的结构序列一定是递增序列，在中序遍历的时候，可以检查当前节点的值时候大于前一个中序遍历到的值即可。

/**
 * 递归实现
 */
static long pre = Long.MIN_VALUE;
public static boolean isValidBST(TreeNode root) {
    if (root == null) {
        return true;
    }
    // 处理左子树   不满足条件就退出
    if (!isValidBST(root.left)){
        return false;
    }
    // 处理根 当前节点：如果当前节点小于等于中序遍历的前一个节点 说明不满足
    if (root.val <= pre){
        return false;
    }
    pre = root.val;
    // 处理右子树
    return isValidBST(root.right);
}

考虑一下迭代怎么写呗：

/**
 * 迭代实现
 *
 * @param root
 * @return
 */
public static boolean isValidBST2(TreeNode root) {
    // 校验参数
    if (root == null){
        return true;
    }
    int pre = Integer.MIN_VALUE;
    // 创建空间
    Deque<TreeNode> stack = new LinkedList<TreeNode>();
    // 根节点入栈  不断的循环遍历
    while(!stack.isEmpty() && root != null){
        // 左
        while(root != null){
            stack.push(root);  // 这里没有offer
            root = root.left;
        }
        //中
        root = stack.pop();
        // 如果中序遍历中得到的节点值小于等于前一个节点值 pre 说明不是二叉搜索树
        if (root.val <= pre){
            return false;
        }
        pre = root.val;
        root =  root.right;
    }
    return true;
}

这个题要是弄明白了，感兴趣的话可以继续研究。

推荐题目⭐⭐⭐⭐⭐：

530. 二叉搜索树的最小绝对差 - 力扣（LeetCode）

---

总结

提示：二分查找；中序遍历；算法小技巧；搜索树问题；平方根优化