排序算法：基数排序与计数排序

基数排序是基于计数排序的算法，每次都需要使用计数排序从而实现基数排序。

那么什么叫基于计数排序？我们首先要明白基数排序的原理：

        每次对数字的一个数位（个位、十位、百位......）进行比较，每次比较后进行一个排序，注意，我们需要保证每次排序后元素的前后位置不变（这点非常关键），为什么说这点非常关键？因为只有第一次排序后相对位置没有变化，才能保证后面比较十位的数（百位等）时，顺序是正确的。那么其实我们的难点也就在于怎么保证比较前后元素的相对位置没有改变。相信很多小火罐们看这篇文章就是为找到这个方法，那么我们就一起来探讨一下吧。

        每次对个位、十位、百位等排序，实质上就是每一个位数进行一次计数排序，那么基数排序算法就是很多次计数排序算法。

        我们就看一看计数排序算法究竟是怎么排的：

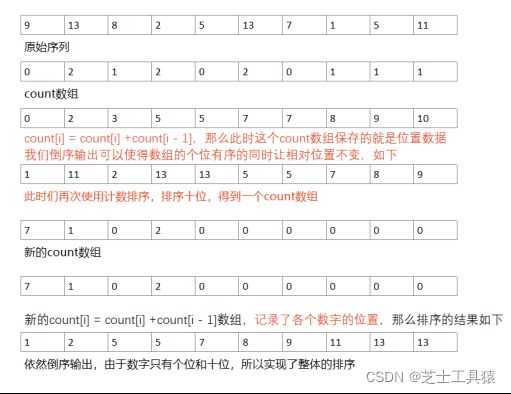
我们给出了一组记录：9、13、8、2、5、13、7、1、5、11，我们就使用计数来看一下：

         我们来解释一下上面的图，第一次我们是对个位数进行了一次计数，将每个位数出现的次数统计到count数组里。count[i]里的i，就是我们的位数值，那么我们就实现了个位数的统计，但是只有这个是什么也做不了的，因为我们此时并不能输出排序结果，试想一下，两个个位是1，那到底怎么排？

所以我们需要进行一个操作：count[i] = count[i] +count[i - 1]

        这步操作的目的是什么？主要就是找到相对位置，这样计算的结果也在上面的图中，来解释一下：倒序输出可以使排序有序（为什么不是正着输出？要思考这个问题，因为我们要让相对位置不变，倒序输出就可以做到这一点），输出结果就如上图，再次对十位进行计数排序，就完成了全部的排序。

        所以，理解基数排序的关键是理解计数排序，理解计数排序的关键是理解count[]数组。理解count[]数组的关键就在于理解count[i] = count[i] +count[i - 1]，最终，也就是理解了count[i] = count[i] +count[i - 1]就搞明白了基数排序。而这一步的操作是确定各个元素的大概位置，然后进行输出，说到这里，不知你是否搞明白了它是如何实现相对位置不变的呢？如果还没很清楚，可以看一看代码里的注释。

        就是确定每个位数的大概位置，然后倒序输出，就能保证每个数字有序。

基数排序算法：

//找到整个序列中的最大值
int getMax(int array[])//用来确定位数（如果每个数位数相同，则不需要此函数）
{
	int i, max = array[0];
	for (i = 1; i < MAX; i++)
		if (array[i] > max)
			max = array[i];
	return max;
}
//计数排序
void RadixSort(int array[], int place) 
{
	int i, output[MAX];//初始化一个数组,记录各个元素
	int count[10] = { 0 };
	for (i = 0; i < MAX; i++)
		count[(array[i] / place) % 10]++;
	//累加 count 数组中的出现次数
	for (i = 1; i < 10; i++)  //核心是找到count数组
		count[i] += count[i - 1];//新count数组表示位置信息即所在位置范围
	//根据 count 数组中的信息，找到各个元素排序后所在位置，存储在 output 数组中
	for (i = MAX - 1; i >= 0; i--) 
	{
		output[count[(array[i] / place) % 10] - 1] = array[i];//count[i]可不是i，而是i的位置范围
		//count[(array[i] / place) % 10] - 1 --> 
		//排序后的正确位置，同一数据的最后一个元素必在最后的位置 1 4 5 1 4 5 1 --> 1 1 1 4 4 5 5
		//由于每次倒着取，就能保证在后面的数据还在后面，即稳定性
		count[(array[i] / place) % 10]--;//已经找出一个数，则此数的范围缩减1
	}
	for (i = 0; i < MAX; i++)
		array[i] = output[i];//把第一次排序后的数组重新赋值给array[i]
}
//基数排序算法（基于计数）
void radixSort(int array[])
{
	int place, max = getMax(array);//找到序列中的最大值
	for (place = 1; max / place > 0; place *= 10)
		RadixSort(array, place);//每次都使用上次已经排序的数组
}

针对基数排序：

        我们首先需要确定最大位数是多少，所以需要把数组中的最大值找到，而后我们利用这个最大值，在基数排序算法中每次都赋一个新的place来传给计数排序算法（place从1开始传值，这样可以保证第一次计数排序比较的是个位数，而后每次增大10倍，保证依次比较十位、百位、千位和万位）。

        而计数排序，就需要一个count数组来记录每次一个数字出现的次数（0-9出现的次数），只有count数组是没用的，我们需要进行一步操作，即count[i] = count[i] +count[i - 1]，这样就能得到每个位数的位置关系了。

        利用这个位置关系，我们倒着输出数组中的元素才能保证它是有序和稳定的，不然就无法正确排序。只有倒着输出，每个数才能真正的找到自己的位置。

        找到位置之后，我们把这个新的数组重新赋值，再次传给基数排序算法来使用计数排序算法从而计算下一个数位。这样每次都可以得到正确的序列，最终得到正确排序的数组。

希望本文对你理解基数排序能有所帮助。