python深度优先搜索算法解决骑士周游问题
python深度优先算法解决骑士周游问题
- 介绍
-
- 问题简介
- 算法
- 实现
-
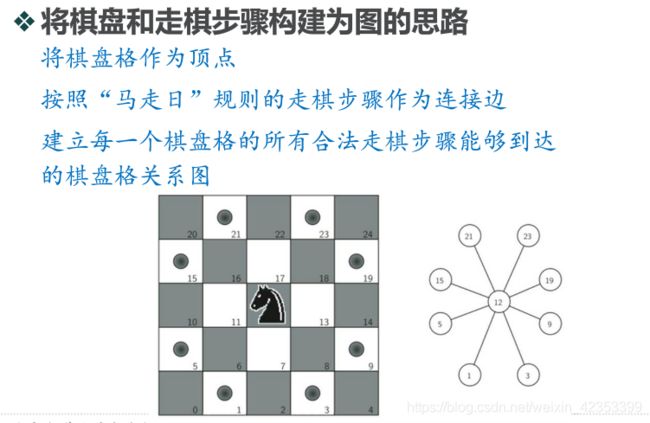
- 形成合法次序图
- 寻找路径
- 改进算法
- 结果
- 代码
介绍
参考资料:
中国大学MOOC的数据结构与算法Python版
常用算法设计方法(6)——贪婪法
问题简介
骑士周游问题,是算法设计中的经典问题。
其一般的问题描述是:考虑nn大小的国际象棋棋盘上某个位置的一只马,按照马走“日”的规则,它是否可能只走nn-1步,正好走过除起点外的其他n*n-1个位置各一次?如果有一种这样的走法,则称所走的这条路线为一条马的周游路线。试设计一个算法找出这样一条马的周游路线。
算法
采用图的深度优先搜索算法解决。
解决方分为两步:
1、将合法走棋的次序表示为一个图。
2、采用图搜索算法搜寻一个长度为(行*列-1)的路径,路径上包含每个顶点恰一次。
深度优先搜索(Depth First Search,DFS),其过程简要来说是对每一个可能的分支路径深入到不能再深入为止,而且每个节点只能访问一次。
深度优先遍历图的方法是,从图中某顶点v出发:
(1)访问顶点v;
(2)依次从v的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和v有路径相通的顶点都被访问;
(3)若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶点均被访问过为止。

时间复杂度为 O ( k n ) , n 为 棋 盘 格 数 目 。 O(k^n),n为棋盘格数目。 O(kn),n为棋盘格数目。
例如:

改进:
Warnsdoff算法:也是一种贪婪法,改变了遍历下一个节点的次序,边数少的节点先被搜索,提升了算法的实际性能。
实现
形成合法次序图
def knightGraph(bdSize):#形成无向图
ktGraph = nx.Graph()
for row in range(bdSize):
for col in range(bdSize):
nodeId = posToNodeId(row,col,bdSize)
newPositions = genLegalMoves(row,col,bdSize)
for e in newPositions:
nid = posToNodeId(e[0],e[1],bdSize)
ktGraph.add_edge(nodeId,nid,color='black')
return ktGraph
def posToNodeId(row,col,bdSize):#节点标签:根据位置定义
return row*bdSize+col
def genLegalMoves(x,y,bdSize):#从位置(x,y)出发,可到达的位置
newMoves = []
moveOffsets = [(-1,-2),(-1,2),(-2,-1),(-2,1),
( 1,-2),( 1,2),( 2,-1),( 2,1)]
for i in moveOffsets:
newX = x + i[0]
newY = y + i[1]
if legalCoord(newX,bdSize) and legalCoord(newY,bdSize):
newMoves.append((newX,newY))
return newMoves
def legalCoord(x,bdSize):#是否超出棋盘范围
if x >= 0 and x < bdSize:
return True
else:
return False
寻找路径
def knightTour(n,path,u,limit):
kg.node[u]['color']='gray'#已遍历到此节点
#u.setColor('gray')
path.append(u)#加入到队列中
if n < limit:#未搜索到一条可行路径
nbrList = list(kg.neighbors(u))#下一个可搜索的节点集合
i = 0
done = False
while i < len(nbrList) and not done:
if kg.node[nbrList[i]]['color'] == 'white':#节点未经过
done = knightTour(n+1, path, nbrList[i], limit)
i = i + 1
if not done: # prepare to backtrack
path.pop()
kg.node[u]['color']='white'#设置成未搜索
#u.setColor('white')
else:
done = True
return done
改进算法
def orderByAvail(n):#排序,边少的点优先
resList = []
for v in kg.neighbors(n):
if kg.node[v]['color'] == 'white':#计算未走过的节点的所连接边的个数
c = 0#计数
for w in kg.neighbors(v):
if kg.node[w]['color'] == 'white':
c = c + 1
resList.append((c,v))
resList.sort(key=lambda x: x[0])#按边的个数从小到大排序
return [y[1] for y in resList]
def knightTourBetter(n,path,u,limit): #use order by available function
kg.node[u]['color']='gray'
#u.setColor('gray')
path.append(u)
if n < limit:
nbrList = orderByAvail(u)
i = 0
done = False
while i < len(nbrList) and not done:
if kg.node[nbrList[i]]['color'] == 'white':
done = knightTourBetter(n+1, path, nbrList[i], limit)
i = i + 1
if not done: # prepare to backtrack
path.pop()
kg.node[u]['color']='white'
else:
done = True
return done
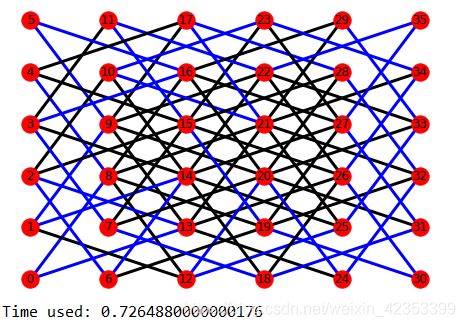
结果
无向图:

深度优先搜索:
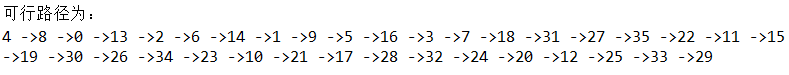
改进算法:
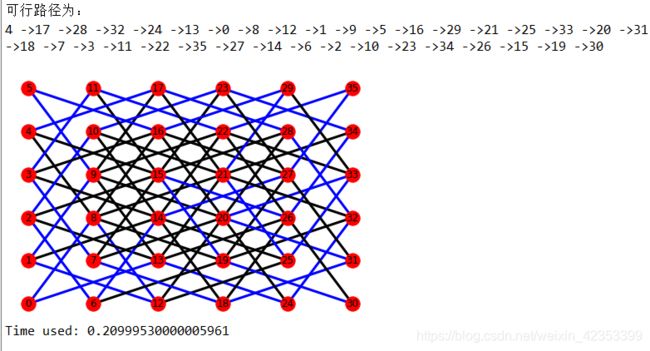
由结果可知:改进后算法运行时间约为原算法的1/3。
代码
import networkx as nx
import matplotlib.pyplot as plt
import time
start1 = time.clock()
#print(start)
def knightGraph(bdSize):#形成无向图
ktGraph = nx.Graph()
for row in range(bdSize):
for col in range(bdSize):
nodeId = posToNodeId(row,col,bdSize)
newPositions = genLegalMoves(row,col,bdSize)
for e in newPositions:
nid = posToNodeId(e[0],e[1],bdSize)
ktGraph.add_edge(nodeId,nid,color='black')
return ktGraph
def posToNodeId(row,col,bdSize):#节点标签:根据位置定义
return row*bdSize+col
def genLegalMoves(x,y,bdSize):#从位置(x,y)出发,可到达的位置
newMoves = []
moveOffsets = [(-1,-2),(-1,2),(-2,-1),(-2,1),
( 1,-2),( 1,2),( 2,-1),( 2,1)]
for i in moveOffsets:
newX = x + i[0]
newY = y + i[1]
if legalCoord(newX,bdSize) and legalCoord(newY,bdSize):
newMoves.append((newX,newY))
return newMoves
def legalCoord(x,bdSize):#是否超出棋盘范围
if x >= 0 and x < bdSize:
return True
else:
return False
def knightTour(n,path,u,limit):
kg.node[u]['color']='gray'#已遍历到此节点
#u.setColor('gray')
path.append(u)#加入到队列中
if n < limit:#未搜索到一条可行路径
nbrList = list(kg.neighbors(u))#下一个可搜索的节点集合
i = 0
done = False
while i < len(nbrList) and not done:
if kg.node[nbrList[i]]['color'] == 'white':#节点未经过
done = knightTour(n+1, path, nbrList[i], limit)
i = i + 1
if not done: # prepare to backtrack
path.pop()
kg.node[u]['color']='white'#设置成未搜索
#u.setColor('white')
else:
done = True
return done
def orderByAvail(n):#排序,边少的点优先
resList = []
for v in kg.neighbors(n):
if kg.node[v]['color'] == 'white':#计算未走过的节点的所连接边的个数
c = 0#计数
for w in kg.neighbors(v):
if kg.node[w]['color'] == 'white':
c = c + 1
resList.append((c,v))
resList.sort(key=lambda x: x[0])#按边的个数从小到大排序
return [y[1] for y in resList]
def knightTourBetter(n,path,u,limit): #use order by available function
kg.node[u]['color']='gray'
#u.setColor('gray')
path.append(u)
if n < limit:
nbrList = orderByAvail(u)
i = 0
done = False
while i < len(nbrList) and not done:
if kg.node[nbrList[i]]['color'] == 'white':
done = knightTourBetter(n+1, path, nbrList[i], limit)
i = i + 1
if not done: # prepare to backtrack
path.pop()
kg.node[u]['color']='white'
else:
done = True
return done
#n=int(input("棋盘大小:"))
n=6
kg = knightGraph(n) #five by five solution
pos=[]
for i in range(n):
for j in range(n):
pos.append((i,j))
nx.draw(kg, pos, with_labels=True)#画出无向图
plt.show()
thepath = []#路径
for i in range(n*n):
kg.node[i]['color'] = 'white'
start = 4#开始节点
knightTour(0,thepath,start,n*n-1)
print("可行路径为:")
for i in range(len(thepath)):#输出路径
if i!=len(thepath)-1:
print(thepath[i],end=' ->')
kg[thepath[i]][thepath[i+1]]['color'] = 'blue'
else:
print(thepath[i])
nx.draw(kg,pos,with_labels=True,width=3,edge_color=[(v['color']) for x,y,v in kg.edges(data=True)])#
#走过的边为蓝色,没走过为黑色
#nx.draw_networkx(kg,pos,with_labels=True,edge_color='blue')
#nx.draw(kg,pos,with_labels=True,width=3,edge_color=(2,255,0))
plt.show()
#print(time.clock())
elapsed = (time.clock() - start1)
print("Time used:",elapsed)