Hyperloglog
一,前言
在互联网行业中存在两个比较重要的指标:PV(页面访问量)和 UV(用户访问量)
如果有这样的一个业务:
统计PV,那么你会怎么做?
我们可以使用Redis的incr、incrby指令,给每个网页配置一个独立Redis计数器就可以了,把这个技术区的key后缀加上当它的日期,这样一个请求过来,就可以通过执行incr、incrby指令统计所有PV。
那么统计UV又该怎么做呢?
UV和PV不同,UV需要对同一用户的访问进行去重,此时很快就能想到使用Redis中的set来存储,但是会面临以下问题:
- 对于数据量越来越大,存储数据的空间占用越来越大
- 统计的性能比较慢,虽然可以通过异步方式统计,但是性能并不理想
因此引入了Redis的新数据类型HyperLogLog。
二,Hyperloglog简介
HyperLogLog 是一种概率数据结构,用于在恒定的内存大小下估计集合的基数(不同元素的个数)。它不是一个独立的数据类型,而是一种特殊的 string 类型,它可以使用极小的空间来统计一个集合中不同元素的数量,也就是基数。在Redis中,每个HyperLogLog键只需要花费12KB内存,就可以计算接近2^64个不同的基数。(为什么是12KB呢?下面会详细讲解)
hyperloglog 类型的底层实现是 SDS(simple dynamic string),它和 string 类型相同,只是在操作时会使用一种概率算法来计算基数。hyperloglog 的误差率为 0.81%,也就是说如果真实基数为 1000,那么 hyperloglog 计算出来的基数可能在 981 到 1019 之间
三,Redis中Hyperloglog的使用
PFADD key element [element …]
将任意数量的元素添加到指定的 HyperLogLog 里面,当PFADD key element [element …]指令执行时,如果HyperLogLog的估计近似基数在命令执行之后出现了变化,那么命令返回1,否则返回0,如果HyperLogLog命令执行时给定的键不存在,那么程序将先创建一个空的HyperLogLog结构,再执行命令。
该命令可以只给定key不给element,这种以方式被调用时:
如果给定的键存在且已经是一个HyperLogLog,那么这种调用不会产生任何效果
如果给定的键不存在,那么命令会创建一个空的HyperLogLog,并且给客户端返回1
返回值:
如果HyperLogLog数据结构内部存储的数据被修改了,那么返回1,否则返回0
时间复杂度:O(1)
PFCOUNT key [key …]
PFCOUNT 指令后面可以跟多个key,当PFCOUNT key [key …]命令作用于单个键时,返回存储在给定键的HyperLogLog的近似基数,如果键不存在,则返回0;当PFCOUNT key [key …]命令作用于多个键时,返回所给定HyperLogLog的并集的近似基数,这个近似基数是通过将索引给定HyperLogLog合并至一个临时HyperLogLog来计算得出的。
返回值:返回给定HyperLogLog包含的唯一元素的近似数量的整数值
时间复杂度:当命令作用于单个HyperLogLog时,时间复杂度为O(1),并且具有非常低的平均常数时间。当命令作用于N个HyperLogLog时,时间复杂度为O(N),常数时间会比单个HyperLogLog要大的多。
PFMERGE destkey sourcekey [sourcekey …]
将多个HyperLogLog合并到一个HyperLogLog中,合并后HyperLogLog的基数接近于所有输入HyperLogLog的可见集合的并集,合并后得到的HyperLogLog会被存储在destkey键里面,如果该键不存在,那么命令在执行之前,会先为该键创建一个空的HyperLogLog。
返回值:字符串回复,返回OK
时间复杂度:O(N),其中N为被合并的HyperLogLog的数量,不过这个命令的常数复杂度比较高
四,Hyperloglog原理
Hyperloglog基于概率论中的伯努利试验并结合了极大似然估算方法,并进行了分桶优化。
1. 伯努利试验
在认识为什么Hyperloglog能够使用极少的内存(12K)来统计巨量的数据之前,先认识一下伯努利试验。
伯努利试验是数学概率论中的一部分内容,它的典故来源于抛硬币。
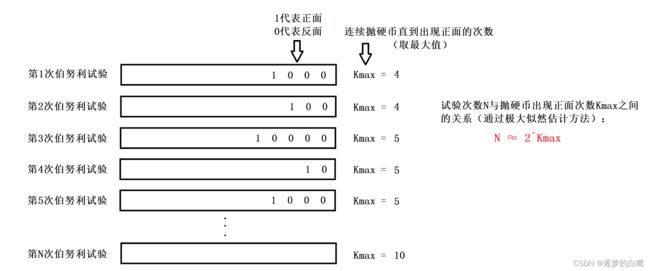
硬币拥有正反两面,一次的上抛至落下,最终出现正反面的概率都是50%。假设一直抛硬币,直到它出现正面为止,我们记录为一次完整的试验,间中可能抛了一次就出现了正面,也可能抛了4次才出现正面。无论抛了多少次,只要出现了正面,就记录为一次试验。这个试验就是伯努利试验。
那么对于多次的伯努利试验,假设这个多次为n次。就意味着出现了n次的正面。假设每次伯努利试验所经历了的抛掷次数为k。第一次伯努利试验,次数设为k1,以此类推,第n次对应的是kn。
其中,对于这n次伯努利试验中,必然会有一个最大的抛掷次数k,例如抛了12次才出现正面,那么称这个为k_max,代表抛了最多的次数。
伯努利试验容易得出有以下结论:
- n 次伯努利过程的投掷次数都不大于 k_max。
- n 次伯努利过程,至少有一次投掷次数等于 k_max
上述案例可以看出,假设n=3,此时通过估算关系n=2^kmax,2^5 ≠3,而且偏差很大。因此得出结论,这种估算方法误差很大。
2. 估值优化
关于上述估值偏差较大的问题,可以采用如下方式结合来缩小误差:
- 增加测试的轮数,取平均值。假设三次伯努利试验为1轮测试,我们取出这一轮试验中最大的的kmax作为本轮测试的数据,同时我们将测试的轮数定位100轮,这样我们在100轮实验中,将会得到100个kmax,此时平均数就是(k_max_1 + … + k_max_m)/m,这里m为试验的轮数,此处为100.
- 增加修正因子,修正因子是一个不固定的值,会根据实际情况来进行值的调整。
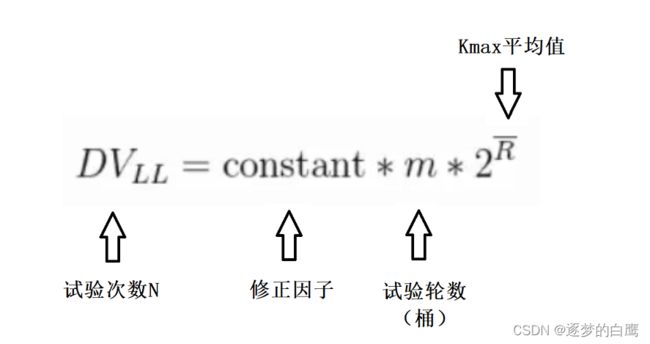
上述这种增加试验轮数,取Kmax的平均值的方法,是loglog算法的实现。因此loglog它的估算公式如下:
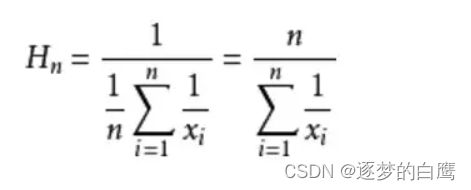
loglog与Hyperloglog的区别在于:loglog采用算数平均数,而Hyperloglog采用调和平均数
调和平均数:
调和平均数的效果更好,例如以下例子:
一个小区内有100户,现在要统计小区的平均工资,小区的工资可以分为大致6000左右,10000左右的,还有一户100000000以上。
此时使用算数平均会导致结果和现实相差很大。
使用调和平均:那户工资上100000000的,对整体的影响就几乎可以忽视。
3. Hyperloglog实现原理
图示:
Redis中Hyperloglog前14位进行分桶,后50位进行获取Kmax
3.1 将数据转化为bit串
通过Hash函数,将数据转为64位的比特串,例如输入5,便转为:101。为什么要这样转化呢?
是因为要和抛硬币对应上,比特串中,0 代表了反面,1 代表了正面,如果一个数据最终被转化了 10010000,那么从右往左,从低位往高位看,我们可以认为,首次出现 1 的时候,就是正面。
那么基于上面的估算结论,我们可以通过多次抛硬币实验的最大抛到正面的次数来预估总共进行了多少次实验,同样也就可以根据存入数据中,转化后的出现了 1 的最大的位置 Kmax 来估算存入了多少数据。
3.2 分桶
分桶就是分多少轮。在抛硬币中我们可以将三次实验分为一组,用这一组的Kmax求平均值当作一次的Kmax,这样可以减少误差。
抽象到计算机存储中去,就是存储的是一个以单位是比特(bit),长度为 L 的大数组 S ,将 S 平均分为 m 组,注意这个 m 组,就是对应多少轮,然后每组所占有的比特个数是平均的,设为 P。容易得出下面的关系:
- L = S.length
- L = m * p
- 以 K 为单位,S 占用的内存 = L / 8 / 1024
为什么Hyperloglog大小为12K?
由上图可知:
- 后14位用于分桶,也就是需要2^14 = 16384个桶(0~16383,也就是14位全0~全1)
- 每个桶子需要存储前50位得到的Kmax值(起始开始最多连续零个数),而50位最多有50个0,因此Kmax最大取到50,2^6 = 64 > 50,因此每个桶只需要6个bit位就可以保存Kmax
- 每8个bit位为1字节,每1024字节为1K
综合以上两点:Hyperloglog的大小 = 16384 * 6 / 8 * 1024 = 12K
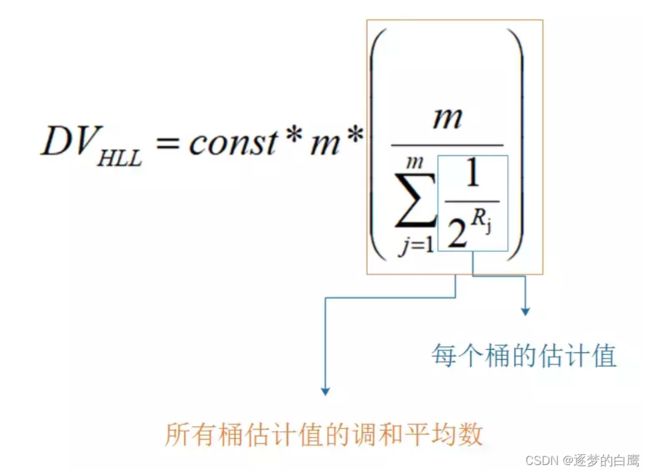
3.3 Hyperloglog估算公式
五,Hyperloglog的优缺点
优点:内存占用很小只有12K
缺点:存在误差概率。不能存储元素本身,只能统计集合基数值。
六,Hyperloglog适用场景
-
统计一个
APP的日活、月活数; -
统计一个页面的每天被多少个不同账户访问量(Unique Visitor,UV);
-
统计用户每天搜索不同词条的个数;
-
统计注册 IP 数。
七,布隆过滤器,布谷鸟过滤器,Hyperloglog如何选择
可以设置误判率:布隆过滤器
可以进行删除操作:布谷鸟过滤器
占用空间小:Hyperloglog