Python中的浮点数探秘

下面的探讨主要针对Python3，在Python2中不一定适用。

查看Python的浮点数如何在内存中存储

Python的浮点数实现原理：
CPython实现有一个PyFloatObject的结构体，用来构造Python的浮点数类型：

typedef struct {
PyObject_HEAD # 这个对象包含：引用计数+对象类型，占8+8=16字节
double ob_fval; # 这个是存储浮点数的地方，Python的浮点数就是C的double，即双精度浮点
} PyFloatObject;

所以Python的浮点数类型占24字节：
引用计数+对象类型+双精度浮点数 = 8+8+8 = 24字节
不过Python3的整数长度无限，所以占字节数不定

用Python代码验证浮点数：

代码：

from ctypes import string_at
from sys import getsizeof
from binascii import hexlify
a=134.375
buffer=hexlify(string_at(id(a),getsizeof(a)))
print(buffer)
buffer_float=buffer[len(buffer)-16:]
print(buffer_float)
tmp=[buffer_float[i:i+2] for i in range(0,len(buffer_float),2)]
tmp=[bin(int(tmp[i].decode(),16))[2:].rjust(8,'0') for i in range(len(tmp)-1,-1,-1)]
print(' '.join(tmp))
print('~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~')
b = ''.join(tmp)
S=b[0]
print('符号位',S)
E=b[1:12]
print('指数位',E)
M=b[12:]
print('尾数位',M)

探讨一下

十进制数 134.375 如何转换为二进制浮点数，并存储在内存中的：

134.375 等于二进制的 10000110.011，转换为IEEE754的浮点数格式：1.0000110011x2^7，其中首位1隐藏，尾数位=0000110011，符号位=0，指数位=(7+1023)的二进制=10000000110

134.375转换二进制小数的方法详见：浮点数在内存中是怎么存储的？

十进制小数部分最后一位不是5时，小数部分与2相乘不会得到1.0，就无法准确转换为二进制，比如134.372，小数0.372如果允许60个二进制位，将转换为：
010111110011101101100100010110100001110010101,100000010000000

整数部分134二进制为：10000110，首位1隐藏，变成0000110(7位)，双精度52位尾数-7位整数部分=45位供小数存储。

因为小数0.372无法准确转换为二进制，第46进行“向偶数舍入”（见 整数转浮点数精度溢出的原因和处理方式），变成：
010111110011101101100100010110100001110010110
010111110011101101100100010110100001110010101,100000010000000 (原60位小数)

用代码验证

import struct
# 134.372 整数部分隐藏首位1 二进制=0000110
# 小数部分向偶数舍入后 二进制=010111110011101101100100010110100001110010110
# 指数二进制=10000000110
# 符号位=0
# S E M = 0,10000000110,0000110(整数)010111110011101101100100010110100001110010110(小数)
# 134.372 64位浮点数实际如下
a = '0100000001100000110010111110011101101100100010110100001110010110'
i = 0
h = ''
while i<64:
    h += f'{int(a[i:i+8],2):x}'
    i+=8
# 134.372 的浮点数十六进制
print(h)  # 4060cbe76c8b4396
# 复原
print(struct.unpack('!d', bytes.fromhex(h)))  # 输出结果是 (134.372,)

十进制数转换浮点数步骤（双精度）

1、整数部分转二进制：可以精确转换，假如数值为134.375

2、小数部分转二进制：可能无法精确转换，当小数最后一位是5时，一定能准确转换，转换后为10000110.011

3、写成规范化形式：1.0000110011x2^7

4、隐藏首位1：变成0000110011，这是尾数部分

5、计算符号位：正数0，负数1

6、计算指数位：双精度浮点数偏移=2^(指数位11-1)-1=1023，指数7+偏移1023=1030=10000000110(二进制)

7、最终内存中的样子：得到符号(S=1位)+指数(E=11位)+尾数(M=52位)的64比特二进制=0,10000000110,0000110011000000000000000000000000000000000000000000

浮点数（双精度）转换十进制数步骤

1、提取尾数位：补全首位的到，1.0000110011000000000000000000000000000000000000000000

2、指数移位操作：指数位10000000110=1030，1030-偏移1023=7，对尾数右移位7（负指数向左移位）=10000110.011000000000000000000000000000000000000000000

3、转换二进制整数+小数部分：1x2^7+0x2^6...0x2^0.0x(2^-1)+1x(2^-2)+1x(2^-3)...=134.375

Python的struct.pack()与struct.unpack()

python的struct主要用来处理C结构数据。主要有如下两个方法：

struct.pack(fmt, v1, v2, …)
struct.unpack(fmt, string)

参考：Python中struct.pack()和struct.unpack()用法详细说明

下面用struct来验证python的浮点数是不是C的double：

可以看到，上面截图的两段代码显示的134.375浮点数的S、E、M是完全一样的。

浮点数的IEEE754标准

有效位计算方法1

一个十进制位需要多少二进制位来表示：

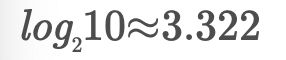
大约需要3.322个二进制位来表示一个十进制位，所以：

单精度浮点数24（23尾数位+1隐藏位）位二进制可以表示大约：24/3.322≈7.225 位的十进制。

可见单精度浮点数的准确有效位是7（有效位表示非零整数部分+小数部分的数字位数，如1.23有效位是3，0.1234有效位是4）。

双精度浮点数的有效位同理计算可得：53/3.322≈15.95，有效位是15，总的来说：

1、单精度浮点数是4字节32位，符号位+指数位+尾数位=1位+8位+23位，有效位7～8位

2、双精度浮点数是8字节64位，符号位+指数位+尾数位=1位+11位+52位，有效位15～16位

参考：浮点数的有效数字位数、浮点数(单精度、双精度数)的有效位、深入理解浮点数有效位

有效位计算方法2

1、单精度浮点数有效数24位全是1时：10^7 < 2^24-1=16777215 < 10^8

所以单精度浮点数能准确表示小数点后第7位，第8位部分准确。16777215是能够转化为单精度浮点数表示的整数的最大精度，超过这个数会进行“舍入”导致丢失精度。

2、双精度浮点数有效数53位全是1时：10^15 < 2^53-1=9007199254740991 < 10^16

所以双精度浮点数能准确表示小数点后第15位，第16位部分准确。9007199254740991是能够转化为双精度浮点数表示的整数的最大精度，超过这个数会进行“舍入”导丢失精度。

参考：理解浮点数的二进制表示、整数转浮点数精度溢出的原因和处理方式、浮点数标准详解参考

Python的sys.float_info详解

sys.float_info输出内容：

In [202]: sys.float_info
Out[202]: sys.float_info(max=1.7976931348623157e+308, max_exp=1024, max_10_exp=308, min=2.2250738585072014e-308, min_exp=-1021, min_10_exp=-307, dig=15, mant_dig=53, epsilon=2.220446049250313e-16, radix=2, rounds=1)

1、max表示的就是最大规约数（即远离0的很大的数，加个负号成为最小规约数）；

2、radix表示的是在电脑中储存的基数，二进制显然是2；

3、max_exp表示的是使得radix**(e-1)为可表示的有限浮点数最大指数，由于移码后的规约数的指数范围为-1022~1023，即最大为1023，所以最大的e自然就是1024；

4、max_10_exp表示的是让10**e为一个可表示的浮点数最大的指数，从结果1.7976931348623157e+308，得出max_10_exp自然就是308；

5、min表示最小的正规约数（即靠近0的很小的数，加个负号为靠近0的负的很大的数）；

6、min_exp表示的是使得radix**(e-1)为可表示的有限浮点数最小指数，移码后的最小指数为-1022（尽管指数为0时，设定偏移量为1022，移码后的指数依然为-1022），因此最小的e为-1021；

7、min_10_exp表示的是让10**e为一个可表示的规约浮点数最小的指数，从结果2.2250738585072014e-308，得出这时最小的e为-307（要注意不是-308，因为10**(-308)比最小正规约数2.2250738585072014e-308还小，这是不符合要求的，所以应该是-307）；

8、dig表示可以保证被精确的转为浮点数的整数的数字个数，保证被精确的转为浮点数的整数应该小于等于9007199254740991，该数有16位数字，但是大于该数的16位数字的整数是无法被精确的转为浮点数的，所以能确保精确的有效位是15；

9、mant_dig就是mantissa digits，即尾数位数，因为尾数的首位1被隐藏，所以真正的尾数位数共有52+1=53位；

10、epsilon表示最小的大于1的浮点数和1之间的差值；

11、rounds表示的是当一个整数转成浮点数，对无法精确表示的整数的近似模式，这里为1表示的是取距离原值最近的浮点数表示；

参考：浮点数的各种最值推算以及对python sys.float_info的解释、整数转浮点数精度溢出的原因和处理方式、python文档

Python浮点数举例

首先，双精度浮点数的全部53有效位可表示的最大十进制数是（53位全是1的情况）：

2**53-1=9007199254740991

看一个更长的小数：

In [220]: 0.123456789123456789

Out[220]: 0.12345678912345678

为什么得到的浮点数是0.12345678912345678？它的小数位有17个，难道有效位变成了17？

其实有效位是16，因为0.12345678912345678中的1234567891234567才是精确的，最后的8是舍入后的值。那为什么是16个有效位？

因为上文说了双精度浮点数有效位15位是精确的，第16位部分精确，而1234567891234567<9007199254740991，1234567891234567这个值并没有完全填满53位尾数，当然是可以的。

舍入的那个值举例：

In [264]: 0.123456789123456749

Out[264]: 0.12345678912345674

In [265]: 0.123456789123456759

Out[265]: 0.12345678912345676

可以明显看到最后一位4或6是舍入值，因为它变大还是变小是不精确的，这取决于浮点数的舍入规则，见 整数转浮点数精度溢出的原因和处理方式