python算法(二)—栈、队列、链表、哈希

---

数据结构：指的是相互之间存在着一种或多种关系的数据元素的集合和该集合中数据元素之间的关系组成。比如，列表、集合和字典等都是一种数据结构。 数据结构的分类

一、栈

栈：限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。

括号匹配问题：给一个字符串，其中包括小括号、中括号、大括号，求该字符串中的括号是否匹配。例如：[(){}[]] 匹配；[]} 不匹配

class Stack:
    def __init__(self):
        self.stack = []

    def push(self, element):  # 进栈
        self.stack.append(element)

    def pop(self):  # 出栈
        return self.stack.pop()

    def get_top(self):  # 获取栈顶元素
        if len(self.stack) > 0:
            return self.stack[-1]
        else:
            return None

    def is_empty(self):
        return len(self.stack) == 0


def brace_match(s):
    match = {')': '(', ']': '[', '}': '{'}
    stack = Stack()
    for ch in s:
        if ch in {'(', '[', '{'}:
            stack.push(ch)
        else:  # ch in {')',']','}'}
            if stack.is_empty():
                return False
            elif stack.get_top() == match[ch]:
                stack.pop()
            else:  # stack.get_top() != match[ch]
                return False
    if stack.is_empty():
        return True
    else:
        return False

s1 = '[]{[]{}()}[]'
s2 = '[)]}'
print(brace_match(s1))
print(brace_match(s2))

二、队列

1、单向队列(Queue)是一个数据集合，仅允许在列表的一端进行插入(队尾)，另一端进行删除(队首)，按先进先出的性质(First-in ,First-out)。
单向队列的实现方式——环形队列：当队尾指针front==Maxsize+1时，再前进一个位置就自动到0。
队首指针前进1：front=(front+1)%Maxsize
队尾指针前进1：rear=(rear+1)%Maxsize
对空条件：rear=front
队满条件：(rear+1)%Maxsize=front

class Queue:
    def __init__(self,size=100):
        self.queue=[0 for _ in range(size)]
        self.size=size
        self.rear=0 #队尾指针
        self.front=0 #队首指针

    #判断队空
    def is_empty(self):
        return self.rear==self.front

    #判断队满
    def is_filled(self):
        return  (self.rear+1)%self.size==self.front

    #进队
    def push(self,element):
        if not self.is_filled():
            self.rear=(self.rear+1)%self.size
            self.queue[self.rear]=element
        else:
            raise IndexError("Queue is filled")

    #出队
    def pop(self):
        if not self.is_empty():
            self.front=(self.front+1)%self.size
            return self.queue[self.front]
        else:
            raise IndexError("Queue is empty")



q=Queue(5)
for i in range(4):
    q.push(i)
print(q.pop())

2、双向队列
两端都支持进队和出队操作

3、Python队列内置模块

from collections import deque
queue=deque()   #创建队列
queue.append(1) #队尾进队
queue.popleft() #队首出队
queue.appendleft(1)  #双向队列首进队
queue.pop() #双向队列队尾出队

如果队满则会自动出队

from collections import deque
queue=deque([1,2,3,4,5],5)
queue.append(6) 
print(queue.popleft())   # —>输出  2

三、栈和队列的应用——迷宫问题

给一个二维列表来表示迷宫（0表示通道，1表示围墙），给出算法求一条走出迷宫的路径。

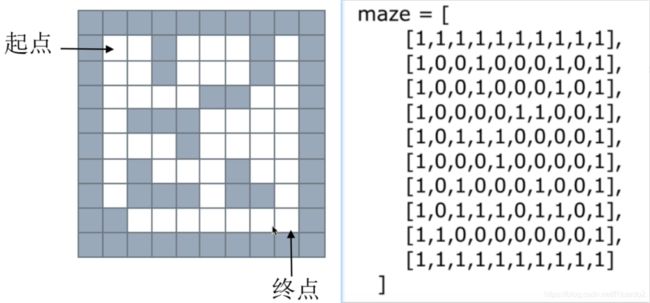
1、栈——深度优先搜索(回溯法)
思路：从一个节点开始，任意找下一个能走的点（不妨默认按上-右-下-左），当找不到能走的点时，退回上一个点寻找是否有其他方向的点。用栈存储当前路径。

maze=[
    [1,1,1,1,1,1,1,1,1,1],
    [1,0,0,1,0,0,0,1,0,1],
    [1,0,0,1,0,0,0,1,0,1],
    [1,0,0,0,0,1,1,0,0,1],
    [1,0,1,1,1,0,0,0,0,1],
    [1,0,0,0,1,0,0,0,0,1],
    [1,0,1,0,0,0,1,0,0,1],
    [1,0,1,1,1,0,1,1,0,1],
    [1,1,0,0,0,0,0,0,0,1],
    [1,1,1,1,1,1,1,1,1,1]
]

#（x,y）：初始位置，dirs表示上下左右移动的位置
dirs=[
    lambda x,y:(x+1,y),
    lambda x,y:(x-1,y),
    lambda x,y:(x,y-1),
    lambda x,y:(x,y+1)
]
def maze_path(x1,y1,x2,y2):#x1,y1初始位置；x2,y2终点位置
    stack=[]
    stack.append((x1,y1))
    while len(stack)>0:
        curNode = stack[-1]  # 当前的节点位置

        #若走到了终点
        if curNode[0]==x2 and curNode[1]==y2:
            for p in stack:
                print(p)
            return True

        # (x,y)向四个方向移动
        for dir in dirs:
            nextNode=dir(curNode[0],curNode[1])
            #判断下一个节点是否能走通
            if maze[nextNode[0]][nextNode[1]]==0:
                stack.append(nextNode)
                maze[nextNode[0]][nextNode[1]]=2    #用2标记已经走过
                break
        else:
            maze[nextNode[0]][nextNode[1]]=2
            stack.pop() #若走不通，则弹出此节点，以返回上一个节点

    else:
        print("没有路")
        return False


maze_path(1,1,8,8)

2、队列——广度优先搜索
用栈做深度搜索并不能保证路线是最短的，因此用队列来进行。
思路：从一个节点开始，寻找所有接下来能继续走的点，继续不断寻找，直到找到出口。使用队列存储当前正在考虑的点。

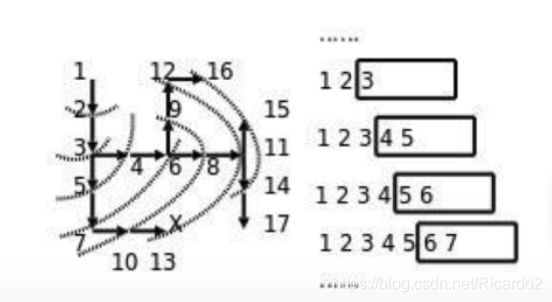
2进队，1进队——>3进队，2出队——>4，5进队，3出队——>6，7进队，4，5出队——>……
然后，将初始位置1下标记为-1；下一个位置2是由上一个位置带入的，其下标为0；……

maze=[
    [1,1,1,1,1,1,1,1,1,1],
    [1,0,0,1,0,0,0,1,0,1],
    [1,0,0,1,0,0,0,1,0,1],
    [1,0,0,0,0,1,1,0,0,1],
    [1,0,1,1,1,0,0,0,0,1],
    [1,0,0,0,1,0,0,0,0,1],
    [1,0,1,0,0,0,1,0,0,1],
    [1,0,1,1,1,0,1,1,0,1],
    [1,1,0,0,0,0,0,0,0,1],
    [1,1,1,1,1,1,1,1,1,1]
]

#（x,y）：初始位置，dirs表示上下左右移动的位置
dirs=[
    lambda x,y:(x+1,y),
    lambda x,y:(x-1,y),
    lambda x,y:(x,y-1),
    lambda x,y:(x,y+1)
]
from collections import  deque

def print_r(path):
    curNode=path[-1]   #终点的位置
    realpath=[]     #真实路径
    while curNode[2]!=-1:
        realpath.append(curNode[0:2])
        curNode=path[curNode[2]]
    realpath.append(curNode[0:2])   #起点
    realpath.reverse()
    for node in realpath:
        print(node)

def maze_path_queue(x1,y1,x2,y2):
    queue=deque()
    queue.append((x1,y1,-1)) #将初始位置下标记作-1
    path=[]
    while len(queue)>0:
        curNode=queue.popleft() #当前节点的位置
        path.append(curNode)
        if curNode[0] == x2 and curNode[1] == y2:   #终点
            print_r(path)
            return True
        for dir in dirs:
            nextNode=dir(curNode[0],curNode[1])
            if maze[nextNode[0]][nextNode[1]]==0:
                queue.append((nextNode[0],nextNode[1],len(path)-1)) #后续可行节点进队，并记录有哪个节点带进来的
                maze[nextNode[0]][nextNode[1]]=2
    else:
        print("没有路")
        return False

maze_path_queue(1,1,8,8)

四、链表

链表是由一系列节点组成的元素集合。每个节点包含两部分，数据域item和指向下一个节点的指针next。通过节点之间的相互连接，最终串联成一个链表。

class Node:
    def __init__(self,item):
        self.item=item
        self.next=None

a=Node(1)
b=Node(2)
c=Node(3)
a.next=b
b.next=c

print('a.item:',a.item)
print('a.next.item:',a.next.item)

输出：
a.item: 1
a.next.item: 2

1、创建链表
头插法：在头节点处插入，插入的节点将成为新的头节点
尾插法：在尾节点处插入，插入的节点将成为新的尾节点

class Node:
    def __init__(self,item):
        self.item=item
        self.next=None

def creat_linklist_head(li):    #头插法
    head=Node(li[0])
    for element in li[1:]:
        node=Node(element)
        node.next=head
        head=node
    return head

def creat_linklist_tail(li):    #尾插法
    head=Node(li[0])
    tail=head
    for element in li[1:]:
        node=Node(element)
        tail.next=node
        tail=node
    return head

def print_linklist(lk):		#链表的遍历
    while lk:
        print(lk.item,end=',')
        lk=lk.next

lk1=creat_linklist_head([1,2,3])
print_linklist(lk1)  #输出3,2,1

lk2=creat_linklist_tail([1,2,3])
print_linklist(lk2) #输出1,2,3

2、节点的插入、删除
插入：4先与2相连，然后1与4相连

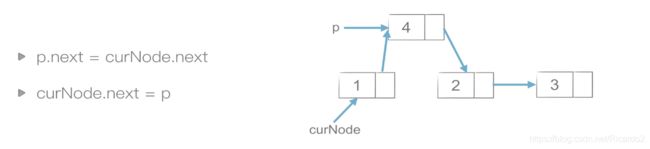
删除：1与2相连，再删除4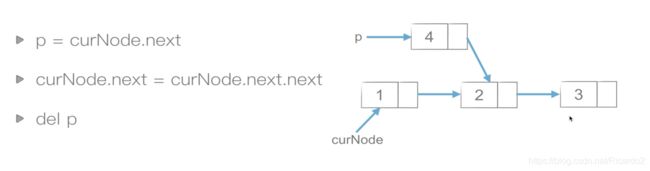3、双链表每个节点有两个指针：一个指向后一个节点，另一个指向前一个节点。

class Node:
    def __init__(self,item):
        self.item=item
        self.next=None
        self.prior=None

插入：

删除：

4、复杂度分析

	顺序表（列表、数组）	链表
按元素值查找	O(n)	O(n)
按下标查找	O(1)	O(n)
在某元素后插入	O(n)	O(1)
删除某元素	O(n)	O(1)

五、哈希表

哈希表是一个通过哈希函数来计算数据存储位置的数据结构，通常支持如下操作：

• insert(key,value)：插入键值对(key,value)
• get(key)：如果存在键为key的键值则返回其value，否则返回空值
• delete(key)：删除键为key的键值对
  1、创建哈希表

class LinkList:  # 定义一个链表类，可支持迭代、插入、寻找、输出为字符串
    class Node:
        def __init__(self, item=None):
            self.item = item
            self.next = None

    class LinkListIterator:  # 设置成可迭代类
        def __init__(self, node):
            self.node = node

        def __next__(self):
            if self.node:
                cur_node = self.node
                self.node = cur_node.next
                return cur_node.item
            else:
                raise StopIteration

        def __iter__(self):
            return self

    def __init__(self, iterable=None):
        self.head = None
        self.tail = None
        if iterable:
            self.extend(iterable)

    def append(self, obj):
        s = LinkList.Node(obj)
        if not self.head:  # 头节点为空时
            self.head = s
            self.tail = s
        else:
            self.tail.next = s
            self.tail = s

    def extend(self, iterable):
        for obj in iterable:
            self.append(obj)

    def find(self, obj):
        for n in self:
            if n == obj:
                return True
            else:
                return False

    def __iter__(self):  # 迭代
        return self.LinkListIterator(self.head)

    def __repr__(self):  # 转换成字符串
        return "<<" + ",".join(map(str, self)) + ">>"


class HashTable:
    def __init__(self, size=101):
        self.size = size
        self.T = [LinkList() for i in range(self.size)]

    def h(self, k):
        return k % self.size

    def find(self, k):
        i = self.h(k)
        return self.T[i].find(k)

    def insert(self, k):
        i = self.h(k)
        if self.find(k):
            print("Duplicated Insert")
        else:
            self.T[i].append(k)


ht = HashTable()
ht.insert(0)
ht.insert(1)
ht.insert(3)
ht.insert(102)
ht.insert(508)
print(",".join(map(str, ht.T)))

print(ht.find(3))