2023.07.16 学习周报

---

摘要

This week, I read a computer science about GNN. At present, GNN is faced with the challenge of sample balance of nodes of different classes. Therefore, the development of GNN for unbalanced node classification is critical, but the work in this area is quite limited. Therefore, a new model framework, GraphSMOTE, is proposed. The framework constructs an embedding space to encode similarities between nodes, thereby synthesizing new samples in that space to maintain authenticity. At the same time, an edge generator is trained to model relational information and provide information for these new samples. This framework is generic and can be easily extended to different variants. By conducting experimental evaluations on three different datasets, the model significantly outperforms other baseline methods. In addition, I learn distance clustering and Euler’s method. Three different distance measurement formulas and the key points of Euler’s method are introduced.

本周，阅读了一篇与GNN相关的文章。目前，GNN 面临不同类别节点样本平衡问题的挑战。因此，开发用于不平衡节点分类的 GNN 至关重要，但这方面的工作却相当有限。为此，提出了一个新的模型框架，GraphSMOTE。该框架构建了一个嵌入空间来编码节点之间的相似性，从而在该空间中合成新的样本以保持真实性。同时，训练一个边缘生成器来建模关系信息，并为这些新样本提供信息。这个框架是通用的，可以轻松扩展到不同的变体。通过在三个不同的数据集上进行实验评估，该模型明显优于其它基线方法。此外，我学习了距离聚类和欧拉法。其中介绍了三种不同的距离度量公式，以及欧拉法的关键点。

---

文献阅读

1.题目

文献链接：GraphSMOTE: Imbalanced Node Classification on Graphs with Graph Neural Networks

2.问题

以前的算法并不适用于图：
1）对产生的新样本，很难生成边关系。过采样技术利用目标示例与其最近邻之间的插值来生成新的训练示例。然而，插值不适合于边，因为它们通常是离散的和稀疏的，插值会 破坏拓扑结构。　
2）产生的新样本可能质量较低。节点属性是高维的，直接对其进行插值很容易生成域外的情况，对训练分类器不利。

3.介绍

如下图所示，图中类不平衡的情况：

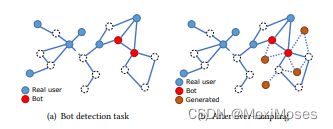
其中：每个蓝色节点表示一个真实用户，每个红色节点表示一个假用户，边表示关系。任务是预测未标记的用户是真还是假。这些类在本质上是不平衡的，因为假用户通常还不到所有用户的1%。半监督设置进一步放大了类不平衡问题，因为只给出了有限的标记数据，这使得标记的少数样本的数量非常小。

在不平衡的节点分类中，多数类主导着损失函数，使得训练后的 GNN 过度分类，无法准确预测样本。目前解决类不平衡问题的方法可以分为：
1）data-level approaches（数据级方法）
2）algorithm-level approaches（算法级方法）
3）hybrid approaches（混合方法）
数据级方法寻求使类分布更加平衡，使用过采样或降采样技术；算法级方法通常对不同的类引入不同的错误分类惩罚或先验概率；混合方法则是将这两者结合起来。

4.Problem definition

使用 G={V,A,F}来表示一个属性网络，其中 V={v1,…,vn}是一组 n 节点。A∈Rn×n
为 G 的邻接矩阵， F∈Rn×d 表示节点属性矩阵，其中 F[j, :]∈R1×d 为节点 j 的节点属性，d 为节点属性的维数。Y∈R^n 是 G 中节点的类信息。

在训练过程中，只有 Y 的一个子集 VL 可用，其中包含节点子集 VL 的标签。总共有 m 类，{C1,…,Cm}。|Ci| 是第 i 类的大小，指的是属于该类的样本数量。我们使用不平衡率 mini(|Ci|)maxi(|Ci|) 来衡量类不平衡的程度。在不平衡设置下，YL 的不平衡比较小。

给定节点类不平衡的 G，以及节点 VL子集的标签，目标是学习一个节点分类器 f ，可适用于多数类和少数类，即：

5.Method

5.1 Feature Extractor

SMOTE用于原始节点特征空间存在的问题：
1）原始特征空间可能是稀疏和高维的，且特征空间不好；
2）未考虑图的结构，可能会导致次优的合成节点。

过采样方法同时考虑了节点表示和拓扑结构，并且遵循了同质性假设。本文研究中使用 GraphSage 作为主干模型结构来提取特征：

5.2 Synthetic Node Generation

对目标少数类的样本与嵌入空间中属于同一类的最近邻样本进行插值。设 h1v 为一个带标记的少数类节点，标记为 Yv。第一步是找到与 h1v 在同一个类中的最近的标记节点，即：

其中，nn(v)是指同一类中 v 的最近邻，可以生成合成节点为：

其中，δ 为一个随机变量，在 [0,1] 范围内呈均匀分布。由于 h1v 和 h1nn(v) 属于同一个类，且非常接近，因此生成的合成节点 h1v′ 也应属同一个类。

5.3 Edge Generator

边生成器是一个加权内积：

其中：Ev,u 为节点 v 和 u 之间的预测关系信息，S 为捕获节点间相互作用的参数矩阵。
边生成器的损失函数为：

此时，并没有合成节点，而是学习一个好的参数矩阵 S。利用边生成器，本文尝试了两种策略：
1）该生成器只使用边重建来进行优化，而合成节点 v′ 的边是通过设置一个阈值 η
生成：

其中：A~是过采样后的邻接矩阵，通过在 A 中插入新的节点和边，并将其发送给分类器。
2）对于合成节点 v′，使用软边而不是二进制边：

A~上的梯度可以从分类器中传播，因此可以同时使用边缘预测损失和节点分类损失对生成器进行优化。

5.4 GNN Classifier

采用另一个 GraphSage 块，在 G~ 上附加一个线性层进行节点分类：

Pv 是节点 v 在类标签上的概率分布，利用交叉熵损失进行优化：

在测试过程中，将节点 v 的预测类设置为概率最高的类 Y′v：

5.5 Optimization Objective

GraphSMOTE 的最终目标函数可以写成：

5.6 算法

6.实验

6.1 数据集

Cora、BlogCatalog、Twitter

6.2 基线

Over-sampling、Re-weight、SMOTE、Embed-SMOTE、GraphSMOTE T、GraphSMOTE O、 GraphSMOTE preT、GraphSMOTE preO

6.3 实验结果

1）不平衡的节点分类

2）过采样量的影响
设置不平平衡率为 0.5，过采样的尺度为 {0.2,0.4,0.6,0.8,1.0,1.2}。

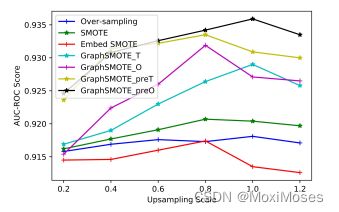
3）不平衡比的影响
设置过采样的尺度为 1，不平衡率为 {0.1,0.2,0.4,0.6}。

4）基础模型的影响
基础模型一个采用 GCN，一个采用 GraphSAGE。

5）参数敏感性分析

7.结论

1）图中节点的类不平衡问题广泛存在于现实任务中，这个问题会显著影响分类器在这些少数类上的性能。
2）提出了一个新的框架GraphSMOTE，它将以前的i.i.d数据过采样算法扩展到这个图设置。
3）GraphSMOTE使用特征提取器构建中间嵌入空间，并在此基础上同时训练边缘生成器和基于GNN的节点分类器。
4）实验证明了它的有效性，并以很大的幅度优于所有其他基线。
5）进行消融研究以了解GraphSMOTE在各种情况下的表现，通过参数敏感性分析，了解GraphSMOTE对超参数的敏感性。

数学建模

1.欧式距离

欧几里得距离，是最常见也是最简单的一种距离，在n维空间下的公式为：

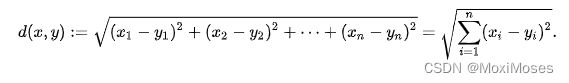
python实现：

import numpy as np
from scipy.spatial.distance import pdist

# 1.欧式距离
x = [1, 1, 1]
y = [3, 4, 5]
xy = np.vstack([x, y])

distance = pdist(xy, metric='euclidean')
print('euclidean distance:', distance)

运行程序结果：

euclidean distance: [5.38516481]

2.切比雪夫距离

切比雪夫距离是向量空间中的一种度量，两点之间的距离定义是其各坐标数值插值绝对值的最大值。公式如下：

python实现：

# 2.切比雪夫距离
x = [1, 1, 1]
y = [3, 4, 5]
xy = np.vstack([x, y])

distance = pdist(xy, metric='chebyshev')
print('chebyshev distance:', distance)

运行程序结果：

chebyshev distance: [4.]

3.曼哈顿距离

用于计算城市的道路距离，由于城市中由一点到达另外一点的通过方式要通过道路来到达，此时两点间的距离不能直接使用欧式距离来计算。公式如下：

python实现：

# 3.曼哈顿距离
x = [1, 1, 1]
y = [3, 4, 5]
xy = np.vstack([x, y])

distance = pdist(xy, metric='cityblock')
print('cityblock distance:', distance)

运行程序结果：

cityblock distance: [9.]

深度学习

1.欧拉法的概念

欧拉法是一种常见的数值解法，用于求解常微分方程。它是数值计算中最简单和最直接的一种方法，常被用于初步探索和近似求解微分方程的数值解。欧拉法的基本思想是将微分方程转化为差分方程，通过迭代逼近连续解。

2.欧拉法的基本步骤

1）确定步长：欧拉法中的步长表示在自变量上的离散间隔。需要根据具体问题和精度要求选择合适的步长。步长越小，数值解的精度越高，但计算量也越大。
2）设定初始条件：为微分方程设置初始条件，即确定在自变量起始点上的函数值。
3）迭代计算：根据微分方程的导数定义，使用差分逼近近似微分方程的解。假设已知当前点上的函数值，通过微分方程得到当前点的导数值，然后将其与步长相乘，并加到当前点上，得到下一个点的函数值。
4）更新自变量：根据设定的步长，更新自变量的值，即从当前点移动到下一个点。
5）重复迭代：重复步骤3和4，直到达到所需的自变量值或时间步长。

3.NS方程与神经网络结合的可能性

1）使用大量的模拟数据来训练神经网络，以达到学习NS方程的解。通过输入的初始状态和边界条件，神经网络可以预测在未来的演变过程中的变化情况。
2）利用神经网络来近似NS方程的解，同时满足NS方程的物理约束。神经网络可以通过学习来预测速度和压力场，同时满足连续性方程和动量方程等物理约束条件，以提高NS方程数值求解的效率和精确度。
3）将NS方程和神经网络结合组成混合模型，就可以用神经网络处理复杂的流动结构或边界层等难以处理的情况，以此提高求解的效率和稳定性。
最后，还需要查阅文献和相关资料继续学习，以此思考挖掘NS方程和神经网络结合的可能性。

---

总结

欧拉法的优点是简单易懂、计算速度快，适用于求解简单的微分方程。然而，它也存在一些缺点。首先，欧拉法的数值解存在误差，特别是当步长较大时，误差会积累导致结果偏离真实解。其次，对于某些复杂的微分方程，欧拉法可能需要很小的步长才能达到足够的精度，从而导致计算量的增加。因此，对于更复杂的微分方程问题，通常会考虑其他更高级的数值解法，提供更准确的数值解。下周，将对欧拉法进行展开学习。