【排序算法】冒泡排序、简单选择排序、直接插入排序比较和分析
【排序算法】冒泡排序、简单选择排序、直接插入排序比较和分析
写在前面:
本文简单介绍了冒泡排序、简单选择排序、直接插入排序,并对这三种排序进行比较,入参都是80000个随机数,比较算法耗时。进一步,我们通过代码分析三种排序算法的性能。
活动地址:CSDN21天学习挑战赛
本文关键字:排序算法、冒泡排序、简单选择排序、直接插入排序、比较和分析、C#
文章目录
- 【排序算法】冒泡排序、简单选择排序、直接插入排序比较和分析
-
-
- 一、排序算法分类
- 二、算法效率
-
- 1. 时间复杂度
- 2. 空间复杂度
- 三、经典排序算法
-
- 1. 简单选择排序
- 2. 冒泡排序
- 3. 直接插入排序
- 四、比较与分析
-
- 1. 算法实现
- 2.比较
- 3.分析
-
- 冒泡排序 VS 直接选择排序
- 直接选择排序 VS 直接插入排序
- 总结
-
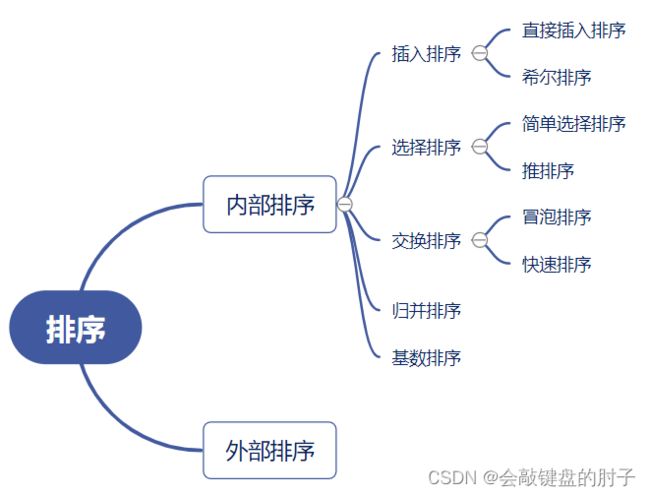
一、排序算法分类
-
内部排序
指将需要处理的所有数据都加载到内部存储器(内存)中进行排序。
-
外部排序
数据量过大,无法全部加载到内存中,需要借助外部存储(文件等)进行排序。
-
常见的分类方法
二、算法效率
1. 时间复杂度
度量一个程序(算法)执行时间的两种方法。
-
事后统计的方法
这种方法可行,但有两个问题:一是要想对设计的算法的运行性能进行评测,需要事件运行该程序;二是所得时间的统计量依赖于计算机的硬件、软件等环境因素。
-
事前估算的方法
通过分析某个算法的时间复杂度来判断哪个算法更优。
-
时间频度
一个算法花费的时间与算法中语句的执行次数成正比。一个算法中的语句执行次数称为语句频度或者时间频度。记为T(n)。
此处引用清华大学《数据结构》课程的一段话,一般情况下,算法中的基本操作语句的重复执行次数是问题规模n的某个函数,用T(n)表示,若有某个辅助函数f(n),使得当n趋近于无穷大时,T(n) / f(n) 的极限值为不等于零的常数,则称f(n)是T(n)的同数量级函数。记作 T(n)=O( f(n) ),称O( f(n) ) 为算法的渐进时间复杂度,简称时间复杂度。
2. 空间复杂度
空间复杂度是对一个算法在运行过程中临时占用存储空间大小的量度。有的算法需要占用的临时工作单元数与解决问题的规模n有关,它随着n的增大而增大,当n较大时,将占用较多的存储单元。
三、经典排序算法
1. 简单选择排序
也称直接选择排序 Select Sorting,整个过程就是每一趟都将无序区中的所有元素进行逐一比较,找到最小的元素,与无序区中的首个元素进行交换,有序区长度加1,无序区长度减1。重复以上步骤,直到所有的元素均已排好。
文章传送门:图解简单选择排序(图解堪比Debug显示每次循环结果)
2. 冒泡排序
冒泡排序的英文Bubble Sort,是一种最基础的交换排序。之所以叫做冒泡排序,因为每一个元素都可以像小气泡一样,根据自身大小一点一点向数组的一侧移动。
文章传送门:图解冒泡排序(多图+解决两种无效比较问题)
3. 直接插入排序
直接插入排序Insertion Sorting是一种最简单的排序方法,过程就是将每个待排元素逐个插入到已经排好的有序序列中。
文章传送门:图解直接插入排序(图解堪比Debug显示每次循环结果)
四、比较与分析
简单选择排序、冒泡排序、直接插入排序的具体内容请至上述三篇博文查看,这里就不展开讲。
本文中的代码分别来自上述三篇博文,并将打印的代码注释(打印会非常影响耗时)。
注意:我们将创建一个随机数组(长度分别为8、800、8000、80000),分别调用三种不同的算法3次,计算耗时。
1. 算法实现
///
/// 简单选择排序静态类
///
public static class SelectSort
{
public static void SelectSortMethod(int[] arr)
{
//选择排序时间复杂度是 O(n^2)
for (int i = 0; i < arr.Length - 1; i++)
{
int minIndex = i;
int min = arr[i];
for (int j = i + 1; j < arr.Length; j++)
{
if (min > arr[j])
{ // 说明假定的最小值,并不是最小
min = arr[j]; // 重置min
minIndex = j; // 重置minIndex
}
}
// 将最小值,放在arr[0], 即交换
if (minIndex != i)
{
arr[minIndex] = arr[i];
arr[i] = min;
}
}
}
}
///
/// 直接插入排序静态类
///
public static class InsertSort
{
public static void InsertSortMethod(int[] arr)
{
int insertVal = 0;
//直接插入排序时间复杂度是 O(n^2)
for (int i = 1; i < arr.Length; i++)
{
//Console.WriteLine($"==============第{i}趟排序==============");
//定义待插入的数
insertVal = arr[i];
int insertIndex = i - 1;
//int count = 0;
// 给insertVal 找到插入的位置
// 说明
// 1. j >= 0 保证在给insertVal 找插入位置,不越界
// 2. insertVal < arr[j] 待插入的数,还没有找到插入位置
// 3. 就需要将 arr[j] 后移
for(int j = i - 1; j >= 0 && insertVal < arr[j]; j--)
{
arr[j + 1] = arr[j];
//count++;
//Console.WriteLine("第" + count + "次后移");
//Console.WriteLine(string.Join(" ", arr));
insertIndex = j - 1;
}
// 当退出循环时,说明插入的位置找到, j + 1
//这里我们判断是否需要赋值
if (insertIndex + 1 != i)
{
arr[insertIndex + 1] = insertVal;
}
//Console.WriteLine("第"+i+ "趟插入");
//Console.WriteLine(string.Join(" ", arr));
}
}
}
///
/// 冒泡排序静态类
///
public static class BubbleSort
{
// 将冒泡排序算法,封装成一个方法
public static void BubbleSortMethod(int[] arr)
{
// 冒泡排序 的时间复杂度 O(n^2)
int temp = 0; // 临时变量
//int count = 0; // 计数比较次数
bool flag = false; // 标识变量,表示是否进行过交换
int lastChangeIndex = 0; //记录最后一次交换的位置
int border = arr.Length - 1; //记录边界,每次比较只需要比到这里为止
for (int i = 0; i < arr.Length - 1; i++)
{
//Console.WriteLine($"==============第{i + 1}趟排序==============");
for (int j = 0; j < border; j++)
{
// 如果前面的数比后面的数大,则交换
if (arr[j] > arr[j + 1])
{
flag = true;
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
lastChangeIndex = j;
}
//count++;
//Console.WriteLine($"第{i + 1}趟第{j + 1}次交换后的数组");
//Console.WriteLine(string.Join(" ", arr));
}
//Console.WriteLine($"第{i + 1}趟排序结果");
//Console.WriteLine(string.Join(" ",arr));
border = lastChangeIndex;
if (!flag)
{
break; // 在一趟排序中,一次交换都没有发生过
}
else
{
flag = false; // 重置flag, 进行下次判断
}
}
//Console.WriteLine($"==============一共比较{count}次==============");
}
}
2.比较
class Program
{
static void Main(string[] args)
{
int n = 80000;
int[] intArray = new int[n];
Random rd = new Random();
for (int i = 0; i < n; i++)
{
intArray[i] = rd.Next(1, n);
}
Console.WriteLine($"=============={n}个数值时耗时==============");
Console.WriteLine($"===============第一次排序================");
Stopwatch Time = new Stopwatch();//实例化计时类
//测试冒泡排序
Time.Restart();
BubbleSort.BubbleSortMethod(intArray);
Time.Stop();
Console.WriteLine("冒泡排序时间 {0}毫秒", Time.Elapsed.TotalMilliseconds);
//测试直接插入排序
Time.Restart();
InsertSort.InsertSortMethod(intArray);
Time.Stop();
Console.WriteLine("直接插入排序时间 {0}毫秒", Time.Elapsed.TotalMilliseconds);
//测试直接选择排序
Time.Start();
SelectSort.SelectSortMethod(intArray);
Time.Stop();
Console.WriteLine("直接选择排序时间 {0}毫秒", Time.Elapsed.TotalMilliseconds);
}
}
==============运行结果===============
==============8个数值时耗时==============
===============第一次排序================
冒泡排序时间 0.201毫秒
直接插入排序时间 0.2019毫秒
直接选择排序时间 0.3448毫秒
==============8个数值时耗时==============
===============第二次排序================
冒泡排序时间 0.1872毫秒
直接插入排序时间 0.1326毫秒
直接选择排序时间 0.2543毫秒
==============8个数值时耗时==============
===============第三次排序================
冒泡排序时间 0.1882毫秒
直接插入排序时间 0.1579毫秒
直接选择排序时间 0.2985毫秒
==========================================
==============800个数值时耗时==============
===============第一次排序================
冒泡排序时间 2.408毫秒
直接插入排序时间 0.2282毫秒
直接选择排序时间 1.2602毫秒
==============800个数值时耗时==============
===============第二次排序================
冒泡排序时间 2.8989毫秒
直接插入排序时间 0.1695毫秒
直接选择排序时间 1.4727毫秒
==============800个数值时耗时==============
===============第三次排序================
冒泡排序时间 1.918毫秒
直接插入排序时间 0.2193毫秒
直接选择排序时间 1.7426毫秒
==========================================
==============8000个数值时耗时==============
===============第一次排序================
冒泡排序时间 265.3872毫秒
直接插入排序时间 0.3355毫秒
直接选择排序时间 87.8721毫秒
==============8000个数值时耗时==============
===============第二次排序================
冒泡排序时间 277.172毫秒
直接插入排序时间 0.2327毫秒
直接选择排序时间 97.9249毫秒
==============8000个数值时耗时==============
===============第三次排序================
冒泡排序时间 263.7068毫秒
直接插入排序时间 0.2201毫秒
直接选择排序时间 85.5911毫秒
==========================================
==============80000个数值时耗时==============
===============第一次排序================
冒泡排序时间 27042.6302毫秒
直接插入排序时间 0.6027毫秒
直接选择排序时间 8270.6628毫秒
==============80000个数值时耗时==============
===============第二次排序================
冒泡排序时间 26427.5526毫秒
直接插入排序时间 1.1142毫秒
直接选择排序时间 8732.2015毫秒
==============80000个数值时耗时==============
===============第三次排序================
冒泡排序时间 26800.8788毫秒
直接插入排序时间 0.7202毫秒
直接选择排序时间 8715.8529毫秒
总结
- 当
n=8时,即随机数组只有8个数值时,三种算法的耗时基本都在0.5ms以内,没有可比性;- 当
n=800时,即随机数组只有800个数值时,可以看出三次比较三种算法中冒泡排序的耗时最长,直接插入排序耗时最短;- 当
n=8000时,即随机数组只有8000个数值时,可以看出冒泡排序的耗时最长,直接插入排序耗时最短,并且冒泡排序的耗时已经是直接选择排序的2倍以上,直接插入排序的耗时与之前基本没有变化;- 当
n=80000时,即随机数组只有80000个数值时,冒泡排序耗时已经达到了30s,直接选择排序耗时9s左右,而直接插入排序耗时基本不变。
3.分析
冒泡排序 VS 直接选择排序
我们通过运行结果可以看出,随着随机数组长度不断增大,冒泡排序算法的耗时增长明显,80000个数组已经达到了30s,直接选择排序耗时要短很多,这主要是因为直接选择排序每趟排序只交换一次,每趟过程中数组没有发生变化,这也是选择排序和冒泡排序的不同之处,冒泡排序一趟会比较至少一次,所以我们所选择排序在性能上优于冒泡排序。
从代码角度我们也可以看到第二次循环的if语句中,冒泡排序的执行语句要比直接选择排序多3条,这也会在一定程度上影响排序的效率。
直接选择排序 VS 直接插入排序
随着随机数组长度不断增大,冒泡排序算法和简单选择排序算法的耗时都有增长,但是直接插入排序的耗时基本没有变化,因为插入排序没有进行交换,都是对数组元素进行后移。
从代码角度我们也可以看到第二次循环的if语句中,直接插入排序的代码也较少,这也会在一定程度上影响排序的效率。
冒泡排序还有其升级版快速排序;
直接插入排序还有折半插入排序和希尔排序;
交换排序和插入排序的比较我们也可以在希尔排序的交换模式和插入模式的比较中看出差异;
这个我们会在后续博文中分析,感兴趣的小伙伴可以订阅一下本专栏。
总结
上述比较是建立的随机数组一致并且仅比较3次的情况下,当出现数组极端情况或者计算机硬件性能差距大的情况时,可能出现与上述结论不一致的情况。并且简单选择排序是不稳定的,直接插入排序在大部分已经排序好的时候表现较好,所以我们不能说冒泡排序一定比其他排序差或者说插入排序一定是最好的。
写在结尾:
文章中出现的任何错误请大家批评指出,一定及时修改。
希望看到这里的小伙伴能给个三连支持!