C++--程序员修炼手册--海量数据处理--位图--布隆过滤器
目录
一,位图是什么:
二,位图怎么实现
2.1,数据处理方法
2.2,位图的实现
1,数据插入操作
2,数据删除操作
3,查找元素
三,布隆过滤器
3.1,布隆过滤器是做什么的:
3.2,布隆过滤器的实现
1,数据插入
2,数据查询
四,哈希切分
五,海量数据面试题
1,哈希切分
2,位图应用
3,布隆过滤器
一,位图是什么:
位图是用来判断某一个数据在不在一个文件里,
优点:是节省空间,效率高,采用哈希映射(直接定址)确定某个数在不在
缺点:是只能判断整数
二,位图怎么实现
2.1,数据处理方法
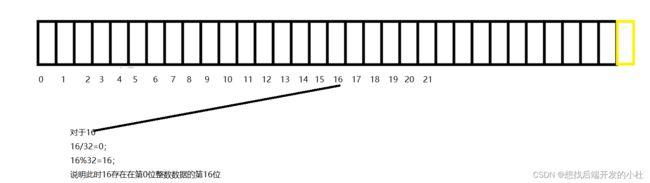
对于一个整数,在32位系统下,占4个字节,我们通过对这个数进行模%32,得到这个数存在哪个数据里,比如对于32,存在第一个整数里面,对66而言,存在第三个数据里面第2位
2.2,位图的实现
1,数据插入操作
使用vector
模板化N值,提前留够存储的位置
把这个数据对应的二进制位置1即可实现将数据插入到位图里面。
//把x对应的位置置1
void set(size_t x)
{
assert(x2,数据删除操作
把这个数据对应的二进制位置0即可实现
void reset(size_t x)
{
assert(x3,查找元素
把元素通过运算,得到具体的位,再把1左移j位,取反,再与当前位置与操作,返回值即可
bool Test(size_t x)
{
assert(x位图代码:
#include
#include
#include
using namespace std;
namespace Etta
{
template
class bitset
{
public:
bitset()
{
_bits.resize(N/32+1,0);
}
//把x对应的位置置1
void set(size_t x)
{
assert(x_bits;
};
void test()
{
bitset<100>bt1;
for(int i=0;i<20;i++)
{
bt1.set(i);
}
for(int j=0;j<20;j++)
{
cout< 一,腾讯面试题:
有不重复的40亿个整数,内存有1GB,如何判断某个数在不在这40亿个整数。
40亿个整数,16G个字节,需要4G空间,如果用排序加二分,内存不够,当我们使用位图存储时,就可以看到,需要4G/8=512m空间,非常节省空间。
三,布隆过滤器
3.1,布隆过滤器是做什么的:
位图只能用于判断整数在不在,而不能实现对string的判断,所以就需要其他的数据结构来判断,此时,布隆提出了过滤器来实现对string的判断,但布隆过滤器因为不能解决多个位的重复指向,所以存在一点误判,所以布隆过滤器允许有误判的情况下才可使用。
优点:时间复杂度O(K),k为哈希函数的个数,
哈希函数之间没有关系,方便硬件并行保存
布隆过滤器不需要存储元素本身,在某些对保密要求比较严格的场合有很大优势
在能够承受一定的误判时,布隆过滤器比其他数据结构有这很大的空间优势
数据量很大时,布隆过滤器可以表示全集,其他数据结构不能
使用同一组散列函数的布隆过滤器可以进行交、并、差运算
缺点:
有误判率,即存在假阳性(False Position),即不能准确判断元素是否在集合中(补救方法:再建立一个白名单,存储可能会误判的数据)
不能获取元素本身
一般情况下不能从布隆过滤器中删除元素
如果采用计数方式删除,可能会存在计数回绕问题
3.2,布隆过滤器的实现
1,数据插入
数据的插入需要将string转换成整形数据再去对这个整形数据进行转换,存入位图里面。
所以需要三个(根据需求)相应的仿函数,为什么需要三个,根据数据量来控制
详细情况--5 分钟搞懂布隆过滤器,亿级数据过滤算法你值得拥有! - 知乎 (zhihu.com)
将位图中的三个位置成1,就代表这个数据存在,通过调用位图实现
代码如下:
void set(const K&key)
{
//使用三个比特位来对应
//将string通过hash算法实现计算成整数
size_t i1=HashBKDR()(key)%N;
size_t i2=HashAP()(key)%N;
size_t i3=HashDJB()(key)%N;
_bitset.set(i1);
_bitset.set(i2);
_bitset.set(i3);
}2,数据查询
与插入一样,先去把要查询的数据通过转换成整数,再去计算每个位,如果都是1,存在,有一个是0,就不存在。
代码如下:
bool Test(const K&key)
{
size_t i1=HashBKDR()(key)%N;
size_t i2=HashAP()(key)%N;
size_t i3=HashDJB()(key)%N;
// 这里3个位都在,有可能是其他key占了,在是不准确的,存在误判
// 不在是准确的
if(_bitset.Test(i1)&&_bitset.Test(i2)&&_bitset.Test(i3))
{
return true;
}
else
{
return false;
}
} 实现代码:
#pragma once
#include"Bitset.h"
struct HashBKDR
{
// "int" "insert"
// 字符串转成对应一个整形值,因为整形才能取模算映射位置
// 期望->字符串不同,转出的整形值尽量不同
// "abcd" "bcad"
// "abbb" "abca"
size_t operator()(const std::string& s)
{
// BKDR Hash
size_t value = 0;
for (auto ch : s)
{
value += ch;
value *= 131;
}
return value;
}
};
struct HashAP
{
// "int" "insert"
// 字符串转成对应一个整形值,因为整形才能取模算映射位置
// 期望->字符串不同,转出的整形值尽量不同
// "abcd" "bcad"
// "abbb" "abca"
size_t operator()(const std::string& s)
{
// AP Hash
register size_t hash = 0;
size_t ch;
for (long i = 0; i < (long)s.size(); i++)
{
ch = s[i];
if ((i & 1) == 0)
{
hash ^= ((hash << 7) ^ ch ^ (hash >> 3));
}
else
{
hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));
}
}
return hash;
}
};
struct HashDJB
{
// "int" "insert"
// 字符串转成对应一个整形值,因为整形才能取模算映射位置
// 期望->字符串不同,转出的整形值尽量不同
// "abcd" "bcad"
// "abbb" "abca"
size_t operator()(const std::string& s)
{
// BKDR Hash
register size_t hash = 5381;
for (auto ch : s)
{
hash += (hash << 5) + ch;
}
return hash;
}
};
template
class BloomFilter
{
public:
void set(const K&key)
{
//使用三个比特位来对应
//将string通过hash算法实现计算成整数
size_t i1=HashBKDR()(key)%N;
size_t i2=HashAP()(key)%N;
size_t i3=HashDJB()(key)%N;
_bitset.set(i1);
_bitset.set(i2);
_bitset.set(i3);
}
//无法实现删除,因为有可能不同的string有相同的位指向
bool Test(const K&key)
{
size_t i1=HashBKDR()(key)%N;
size_t i2=HashAP()(key)%N;
size_t i3=HashDJB()(key)%N;
// 这里3个位都在,有可能是其他key占了,在是不准确的,存在误判
// 不在是准确的
if(_bitset.Test(i1)&&_bitset.Test(i2)&&_bitset.Test(i3))
{
return true;
}
else
{
return false;
}
}
private:
Etta::Bitset _bitset;
};
void BloomTest()
{
// BloomFilter<600>bf;
// bf.set("蜘蛛");
// bf.set("zhuzhu'");
// bf.set("啥呀");
// bf.set("啥压");
// bf.set("说啥");
// bf.set("嗯哼");
//
// cout< bf;
size_t N = 100;
std::vector v1;
for (size_t i = 0; i < N; ++i)
{
std::string url = "https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html";
url += std::to_string(1234 + i);
v1.push_back(url);
}
for (auto& str : v1)
{
bf.set(str);
}
for (auto& str : v1)
{
cout << bf.Test(str) << endl;
}
cout << endl << endl;
std::vector v2;
for (size_t i = 0; i < N; ++i)
{
std::string url = "https://www.cnblogs.com/-clq/archive/2012/05/31/2528153.html";
url += std::to_string(6789 + i);
v2.push_back(url);
}
size_t n2 = 0;
for (auto& str : v2)
{
if (bf.Test(str))
{
++n2;
}
}
cout << "相似字符串误判率:" << (double)n2 / (double)N << endl;
std::vector v3;
for (size_t i = 0; i < N; ++i)
{
std::string url = "https://zhuanlan.zhihu.com/p/43263751";
url += std::to_string(6789 + i);
v3.push_back(url);
}
size_t n3 = 0;
for (auto& str : v3)
{
if (bf.Test(str))
{
++n3;
}
}
cout << "不相似字符串误判率:" << (double)n3 / (double)N << endl;
} 四,哈希切分
先看例题:
给两个文件,分别有100亿个query,我们只有1G内存,如何找到两个文件交集?分别给出精确算法和近似算法
解法:100亿query,假设每个query为20个字节,此时就占用2000亿个字节,需要200G的内存对其管理,而我们只有1G内存,所以就需要对文件进行切分,再处理,
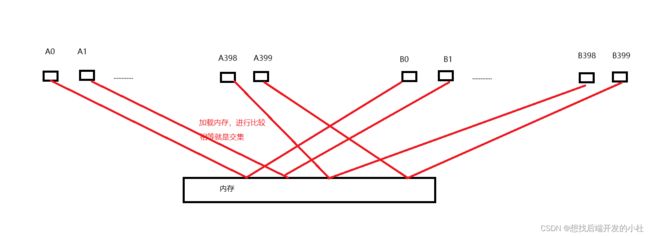
1,切割:首先把A文件切成400份,A0~A399,每个文件有500M空间,然后使用哈希算法,读取文件中每一个query,i=HASHBKDR()(query)%400,然后每个query进入对应的Ai的小文件里面。
2,对B文件进行与A文件相同的操作,此时A文件与B文件相同的query进入了同一个Ai小文件里面
3,读取Ai小文件到内存比较,如果相等,就是交集。
此时,我们就能得出一个具体的解决海量数据的解决方法,切割,运算(hash),加载比较。
哈希切分的特点就是(很重要):A和B相同文件的query进入下表相同的小文件里面
五,海量数据面试题
1,哈希切分
给一个超过100G大小的log file, log中存着IP地址, 设计算法找到出现次数最多的IP地址? 与上题条件相同,如何找到top K的IP?
解法:哈希切分
1,将文件切成100份,此时生成A0~A99个文件,然后读取小文件中的IP,对ip进行哈希算法处理成整数,再用直接定址法,这样就能将相同的ip地址放到对应的Ai小文件中,然后,遍历小文件。统计次数,就可以找到出现最多的ip地址,如果文件小于2G,可以利用map。大于2G,再切分。
 topK,建堆,建一个K个数的小堆,如果统计次数大于k中次数,进堆,退元素。
topK,建堆,建一个K个数的小堆,如果统计次数大于k中次数,进堆,退元素。
2,位图应用
1. 给两个文件,分别有100亿个整数,我们只有1G内存,如何找到两个文件交集?
将每份文件切成100份,A0~A99,B0~B99,使用hash算法,相同整数会被分配同一个下标的小文件之中,再对Ai,Bi小文件进行求交集,将结果汇总,就是文件的交集。
2. 位图应用变形:1个文件有100亿个int,1G内存,设计算法找到出现次数不超过2次的所有整数
使用两个位来处理,两个位都为1,即超过2.
void Set(size_t x)
{
// 00 -> 01
if (!_bs1.Test(x) && !_bs2.Test(x))
{
_bs1.Set(x);
} // 01 -> 10
else if (!_bs1.Test(x) && _bs2.Test(x))
{
_bs1.Set(x);
_bs2.Reset(x);
} // 10 -> 11
else if (_bs1.Test(x) && !_bs2.Test(x))
{
_bs2.Set(x);
}
else
{
// 不处理
}
}
3,布隆过滤器
如何扩展BloomFilter使得它支持删除元素的操作
对位进行计数操作,指向位的数多一个,计数位就加一,删除就技术位减1