数据结构--AVL树（全）
目录
什么是AVL树？
AVL树的特点及形成原因
二叉搜索树基本概念
二叉搜索的特点
二叉搜索树的优点及缺点
改进的二叉搜索树——AVL树
AVL树的定义
AVL树的特点
结点的平衡因子balance
构建一个AVL树的节点
AVL的操作旋转
旋转的基本原理概念
左单旋转
左单旋转的原理
代码展示
右单旋转
右单旋转原理
代码展示
左右双旋转
右左双旋转
代码
AVL确定平衡(回溯法)
分析
代码
AVL树的插入
分析
代码
AVL树的删除
原理
三种情况
case1：
case2：
case3:
代码：
AVL树其他操作
AVL树的最小值
AVL树的最大值
返回某节点的直接前驱节点
返回某节点的直接后继节点
什么是AVL树？
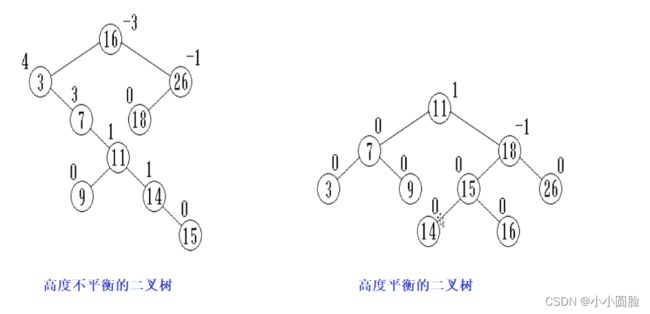
AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。
AVL树的特点及形成原因
AVL树本质上是一棵高度平衡的二叉搜索树；先回顾二叉搜索树的基本概念；
二叉搜索树基本概念
二叉查找树(Binary SearchTree)，(又: 二叉搜索树，二叉排序树)它或者是一棵空树， 或者是具有下列性质的二插树:若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;它的左、 右子树也分别为二叉排序树。二叉搜索树作为一种经典的数据结构,它既有链表的快速插入与删除操作的特点，又有数组快速查找的优势;所以应用十分广泛,例如在文件系统和数据库系统一般会采用这种数据结构进行高效率的排序与检索操作。
二叉搜索的特点
设x是二叉搜索树中的一个结点。如果y是x左子树中的一个结点，那么y.key≤x.key。如果y是x右子树中的一个结点，那么y.key≥x.key。
在二叉搜索树中：
1.若任意结点的左子树不空，则左子树上所有结点的值均不大于它的根结点的值。
2. 若任意结点的右子树不空，则右子树上所有结点的值均不小于它的根结点的值。
3.任意结点的左、右子树也分别为二叉搜索树。
二叉搜索树的优点及缺点
假设用有顺序的数组去如{12,23,34,45,56,67,78,89,90,100}构建一个二叉搜索树如图所示的两种情况：
（1）如果构建的二叉搜索树如图一所示：我们知道想要查找67，只需要搜索3次，这就体现了二叉搜索树的优点了；
（2）如果构建二叉搜索树的数据是顺序的如图二；那就没有体现出来二叉搜索树的优点；为了改进这种情况，就出现了平衡二叉树（AVL）；
改进的二叉搜索树——AVL树
AVL树的定义
一棵AVL树或者是空树，或者是具有下列性质的二叉搜索树:它的左子树和右子树都是AVL树，且左子树和右子树的高度之差的绝对值不超过1。
AVL树的特点
1.本身首先是一棵二叉搜索树。（重点）
2.带有平衡条件：每个结点的左右子树的高度之差的绝对值（平衡因子）最多为1。
也就是说，AVL树，本质上是带了平衡功能的二叉查找树（二叉排序树，二叉搜索树）。
结点的平衡因子balance
●每个结点附加一个数字，给出该结点右子树的高度减去左子树的高度所得的高度差。这个数字即为结点的平衡因子balance。
●根据AVL 树的定义，任一结点的平衡因子只能取-1, 0和1。
●如果一个结点的平衡因子的绝对值大于1,则这棵二叉搜索树就失去了平衡,不再是AVL树。
●如果一棵二叉搜索树是高度平衡的，它就成为AVL树。如果它有n个结点,其高度可保持在0(log,n),平均搜索长度也可保持在
构建一个AVL树的节点
从AVL树的概念来看，我们知道AVL树是二叉搜索树的升级版本吧；也就是增加了平衡因子；我上次说的二叉搜索树的节点图用一下；下图表示二叉搜索树和AVL树节点的不同；
typedef int KeyType;
typedef struct AVLNode
{
struct AVLNode* leftchild;
struct AVLNode* rightchild;
struct AVLNode* parent;
KeyType key;
int balance;
}AVLNode,*AVLTree;为了后面代码的工整和调用简单添加下面代码：
AVLNode* Buynode(KeyType kx)；插入时用来购买一个节点
AVLNode* MakeRoot(KeyType kx)；对申请的节点赋值
AVLNode* Buynode(KeyType kx)
{
AVLNode* s = (AVLNode*)malloc(sizeof(AVLNode));
if (nullptr == s) exit(1);
memset(s, 0, sizeof(AVLNode));
return s;
}
AVLNode* MakeRoot(KeyType kx)
{
AVLNode* root = Buynode(kx);
root->key=kx;
root->balance=0;
return root;
}AVL的操作旋转
旋转的基本原理概念
AVL树的基本操作一般涉及运做同在不平衡的二叉查找树所运做的同样的算法。但是要进行预先或随后做一次或多次所谓的"AVL 旋转"。 假设由于在二叉排序树上插入结点而失去平衡的最小子树根结点的指针为a（即a是离插入点最近，且平衡因子绝对值超过1的祖先结点），则失去平衡后进行进行的规律可归纳为下列四种情况：
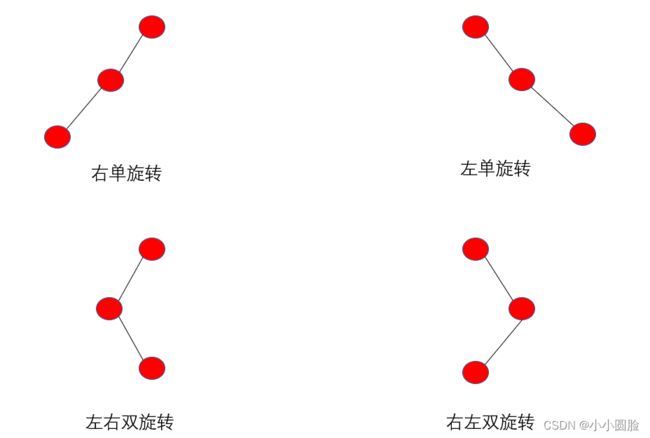
（1）单向右旋平衡处理LL：由于在*a的左子树根结点的左子树上插入结点，*a的平衡因子由1增至2，致使以*a为根的子树失去平衡，则需进行一次右旋转操作；
（2）单向左旋平衡处理RR：由于在*a的右子树根结点的右子树上插入结点，*a的平衡因子由-1变为-2，致使以*a为根的子树失去平衡，则需进行一次左旋转操作；
（3）双向旋转（先左后右）平衡处理LR：由于在*a的左子树根结点的右子树上插入结点，*a的平衡因子由1增至2，致使以*a为根的子树失去平衡，则需进行两次旋转（先左旋后右旋）操作。
（4）双向旋转（先右后左）平衡处理RL：由于在*a的右子树根结点的左子树上插入结点，*a的平衡因子由-1变为-2，致使以*a为根的子树失去平衡，则需进行两次旋转（先右旋后左旋）操作。
左单旋转
左单旋转的原理
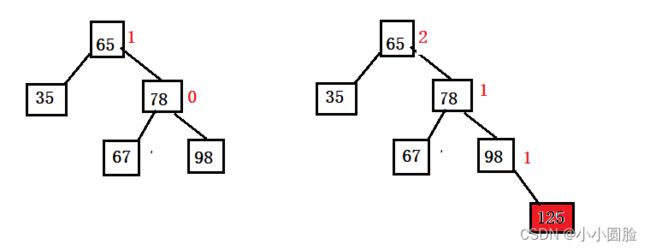
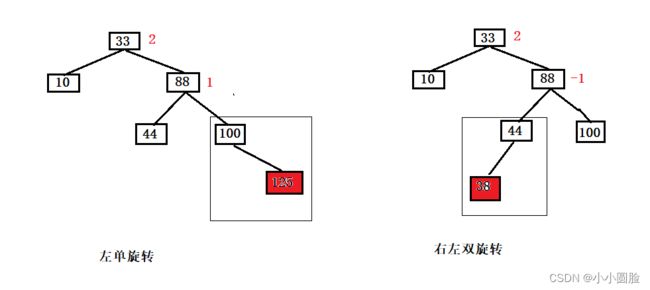
（1）如果插入时的顺序是这样的，如图当插入125时对于这个树来说已经大于2，处于不平衡，所以需要旋转使其平衡；
（2）左旋转的条件出来了，但是旋转时要注意什么？首先它是一个搜索二叉树，所以中序遍历是从小到大的，所以旋转后还是符合二叉搜索树的性质；
代码展示
void RotateLeft(AVLTree& tree, AVLNode* ptr)
{
AVLNode* newroot = ptr->rightchild;
newroot->parent = ptr->parent;
ptr->rightchild = newroot->leftchild;
if (newroot->leftchild != nullptr)
{
newroot->leftchild->parent = ptr;
}
newroot->rightchild = ptr;
if (ptr == tree)
{
tree = newroot;
}
if (ptr != tree)
{
if (ptr->parent->leftchild == ptr)
{
ptr->parent->leftchild = newroot;
}
else
{
ptr->parent->rightchild = newroot;
}
}
ptr->parent = newroot;
}右单旋转
右单旋转原理
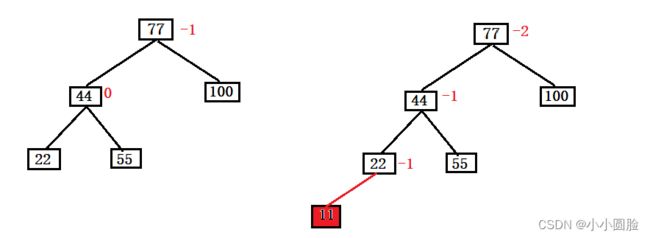
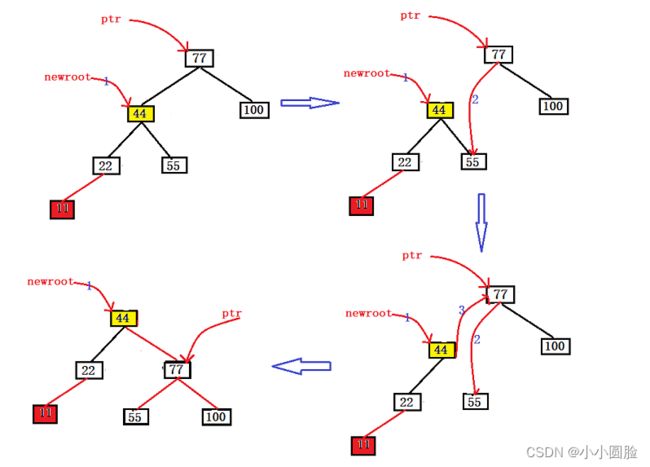
（1）如果插入的顺序是{77,44,100,22,55,11}，则当插入11时，该AVL出现不平衡，需要进行右旋转；
（2）和左旋转一样，顺序如下图，需要注意的是旋转后还必须符合搜索二叉树的性质即中序遍历是从小到大的顺序；
代码展示
void RotateRight(AVLTree& tree, AVLNode* ptr)
{
AVLNode* newroot = ptr->leftchild;
newroot->parent = ptr->parent;
ptr->leftchild = newroot->rightchild;
if (newroot->rightchild != nullptr)
{
newroot->rightchild->parent = ptr;
}
newroot->rightchild = ptr;
if (ptr == tree)
{
tree = newroot;
}
else
{
if (ptr->parent->leftchild == ptr)
{
ptr->parent->leftchild = newroot;
}
else
{
ptr->parent->rightchild = newroot;
}
}
ptr->parent = newroot;
}左右双旋转
我们将左单旋转和左右双旋转，我们可以将其写入左平衡函数中;
（1）对于右单旋转来说 ptr->balance=-1;
（2）对于左右双旋转来说 ptr->balance=1;
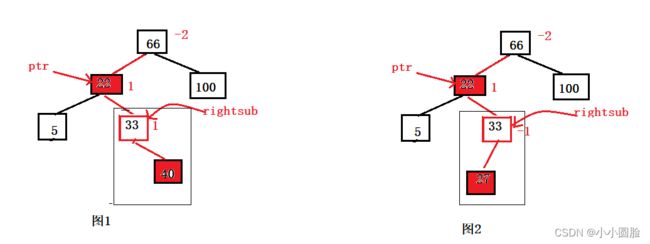
如图所示：
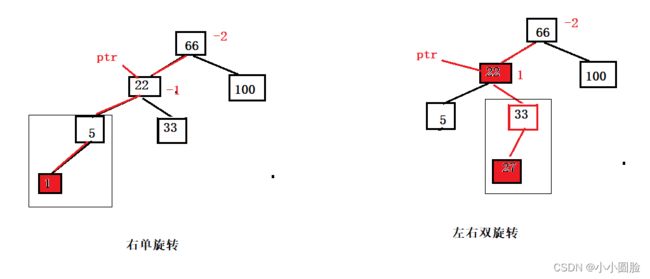对于左右双旋转来说有rightsub=1或者rightsub=-1两种情况如图的1和2；这对我们平衡后改变其平衡因子来说明了；
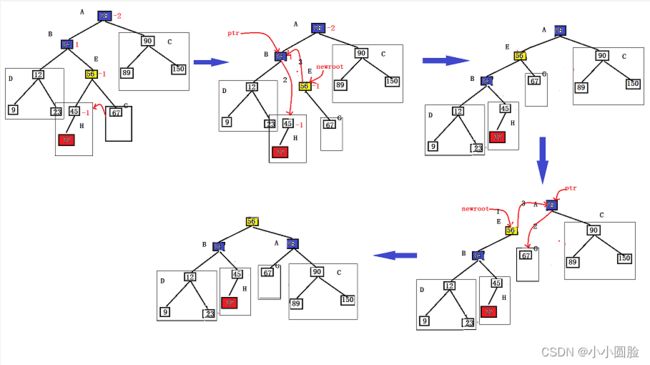
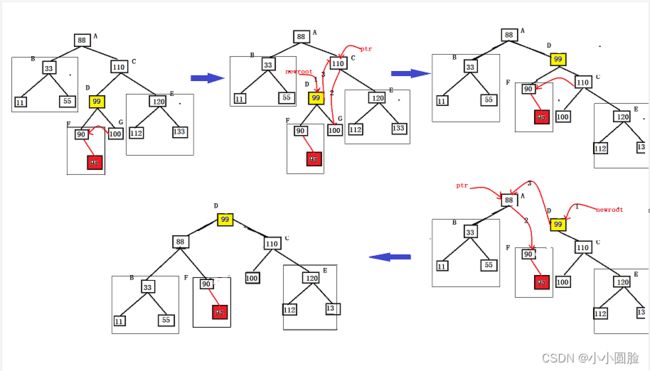
对于左右双旋转来说，实现起来并不那么难，我们只需要调用好左右单旋转就行；如下图所示，先对BEC点进行左旋转，再对AEB节点进行右旋转；
再调用单旋转之前，我们先去修改对应的平衡因子；这个我们只看平衡前后的平衡因子值；
void LeftBalance(AVLTree& tree, AVLNode* ptr)
{
AVLNode* leftsub = ptr->leftchild, * rightsub = nullptr;
switch (leftsub->balance)
{
case 0: cout << "left balance " << endl; break;
case -1:
ptr->balance = 0;
leftsub->balance = 0;
RotateRight(tree, ptr);
break;
case 1:
rightsub = leftsub->rightchild;
switch (rightsub->balance)
{
case -1:
leftsub->balance = 0;
ptr->balance = 1;
break;
case 1:
leftsub->balance = -1;
ptr->balance = 0;
break;
case 0:
leftsub->balance = 0;
ptr->balance = 0;
break;
}
rightsub->balance = 0;
RotateLeft(tree, leftsub);
RotateRight(tree, ptr);
break;
}
}右左双旋转
和上面一样，右左双旋转与左右双旋转是镜像对称关系；
我们将左单旋转和右左双旋转写在一起，称为右平衡函数；如图所示：
（1）对于左单旋转来说 ptr->balance=1;
（2）对于右左双旋转来说 ptr->balance=-1;
对于右左双旋转来说有rightsub=-1或者rightsub=1两种情况如图的1和2；这对我们平衡后改变其平衡因子来说明了；
对于右左双旋转来说，实现起来并不那么难，我们只需要调用好左右单旋转就行；如下图所示，先对CDF点进行右旋转，再对ADC节点进行左旋转；
代码
void RightBalance(AVLTree& tree, AVLNode* ptr)
{
AVLNode* rightsub = ptr->rightchild, * leftsub = nullptr;
switch (rightsub->balance)
{
case 0:cout << "right balance " << endl; break;
case 1:
ptr->balance = 0;
rightsub->balance = 0;
RotateLeft(tree, ptr);
break;
case -1:
leftsub = rightsub->leftchild;
switch (leftsub->balance)
{
case 0:
ptr->balance = 0;
rightsub->balance = 0;
break;
case 1:
ptr->balance = -1;
rightsub->balance = 0;
break;
case -1:
ptr->balance = 0;
rightsub->balance = 1;
break;
}
leftsub->balance = 0;
RotateRight(tree, rightsub);
RotateLeft(tree, ptr);
}
}AVL确定平衡(回溯法)
分析
对于插入的新节点来说，我们从新节点开始开始向根节点开始回溯，进行修改每个节点的平衡因子；因为前面我们已经分类讨论了，所以这里我们进行调用就行；
（1）在左边插入，如果插入节点的父节点的平衡因子为-1，则调用左平衡函数；
（2）在右边插入，如果插入节点的父节点的平衡因子为1，则调用右平衡函数；
代码
void PassBalance(AVLTree& tree, AVLNode* p)
{
AVLNode* pa = p->parent;
bool tall = true;
for (; pa != nullptr && tall;)
{
if (pa->leftchild == p)
{
switch (pa->balance)
{
case 0: pa->balance = -1; break;
case 1: pa->balance = 0;
tall = false;
break;
case -1:
LeftBalance(tree, pa);
tall = false;
break;
}
}
else
{
switch (pa->balance)
{
case 0: pa->balance = 1; break;
case -1: pa->balance = 0;
tall = false;
break;
case 1:
RightBalance(tree, pa);
tall = false;
break;
}
}
p = pa;
pa = p->parent;
}
}AVL树的插入
分析
现在对于我们来说就很简单了；及插入的节点按照搜索二叉树的方式插入就行，最后对插入的节点进行回溯函数调用，如果不平衡我们也不用管，上面函数会自动调用；
代码
bool Insert(AVLNode*& tree, KeyType kx)
{
if (tree == nullptr)
{
tree = MakeRoot(kx);
return true;
}
AVLNode* pa = nullptr;
AVLNode* p = tree;
while (p != nullptr && p->key != kx)
{
pa = p;
p = kx < p->key ? p->leftchild : p->rightchild;
}
if (p != nullptr && p->key == kx) return false;
p = Buynode(kx);
p->parent = pa;
if (kx < pa->key)
{
pa->rightchild = p;
}
else
{
pa->rightchild = p;
}
PassBalance(tree, p);
return true;
}AVL树的删除
原理
（1）如果被删结点x最多只有一个子女，那么问题比较简单。如果被删结点x有两个子女，首先搜 索x在中序次序下的直接前驱y(同样可以找直接后继)。再把结点y的内容传送给结点x，现在 问题转移到删除结点y。把结点y当作被删结点x。
（2）将结点x从树中删去。因为结点x最多有一个子女，我们可以简单地把x的双亲结点中原来指 向 x的指针改指到这个子女结点；如果结点x没有子女；x双亲结点的相应指针置为NULL。然 后将原来以结点x为根的子树的高度减1；
（3）必须沿x通向根的路径反向追踪高度的变化对路径上各个结点的影响。
（4）用一个布尔变量shorter来指明子树的高度是否被缩短。在每个结点上要做的操作取决shorter 的值和结点的balance,有时还要依赖子女的balance。
（5）布尔变量shorter的值初始化为True。然后对于从x的双亲到根的路径上的各个结点p,在 shorter保持为True 时执行下面的操作。如果shorter变成False, 算法终止。
三种情况
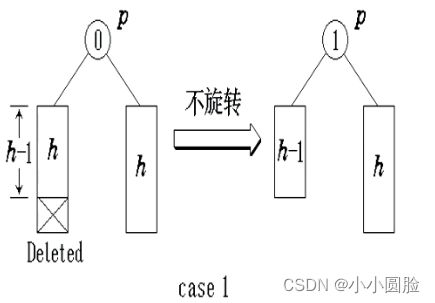
case1：
当前节点p的balance为0。如果它的左子树或右子树被缩短，则它的balance改为1或-1，同时 shorter改为False；
case2：
节点p的balance不为0，且较高的子树被缩短，则p的balance改为0，同时shorter置为True；
case3:
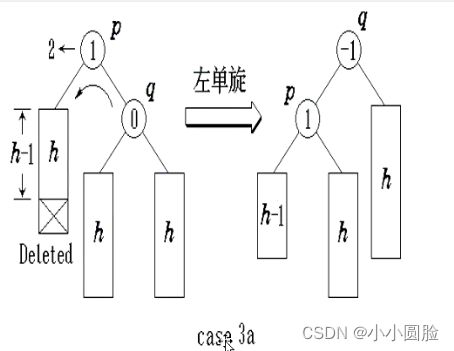
结点p的balance不为0，且较矮的子树又被缩短，则在结点p发生不平衡。需要进行平衡化旋转来恢复平衡。令p的较高的子树的根为q(该子树未被缩短)，根据q的balance,有如下3种平衡化操作。
case3a:如果q的balance为0，执行一个单旋转来恢复结点p的平衡，置shorter 为False。
case3b:如果q的balance与p的balance相同,则执行一个单旋转来恢复平衡，结点p和q的balance均改为0，同时置shorter为True。
case3c:如果p与q的balance相反，则执行一个双旋转来恢复平衡，先围绕q转再围绕p转。新的根结点的balance置为0，其它结点的balance相应处理，同时置shorter为True。
在case 3a, 3b和3c的情形中，旋转的方向取决于是结点p的哪一棵子树被缩短。
代码：
void PasBalance(AVLTree& tree, AVLNode* p)
{
AVLNode* pa = p->parent;
bool tall = true;
for (; pa != nullptr && tall;)
{
if (pa->leftchild == p)
{
switch (pa->balance)
{
case 0: pa->balance = 1;
tall = false;
break;
case 1:
LeftBalance(tree, pa);
tall = false;
break;
case -1:pa->balance = 0;
tall = true;
break;
}
}
else // p -->pa->rightchild
{
switch (pa->balance)
{
case 0: pa->balance = -1; break;
case -1:
RightBalance(tree, pa);
tall = false;
break;
case 1:pa->balance = 0;
tall = true;
break;
}
}
p = pa;
pa = p->parent;
}
}
bool Remove(AVLNode*& ptr, KeyType kx)
{
if (nullptr == ptr)return false;
AVLNode* p = ptr;
while (p != nullptr && p->key != kx)
{
p = kx < p->key ? p->leftchild : p->rightchild;
}
if (p == nullptr)return false;
if (p->leftchild != nullptr && p->rightchild != nullptr)
{
AVLNode* last = First(p->rightchild);
p->key = last->key;
p = last;
}
AVLNode* pa = p->parent;
AVLNode* child = p->leftchild != nullptr ? p->leftchild : p->rightchild;
if (child != nullptr) child->parent = pa;
if (pa == nullptr)
{
pa = child;
}
else
{
if (pa->leftchild == p)
{
pa->leftchild = child;
}
else
{
pa->rightchild = child;
}
}
PasBalance(ptr, p);
free(p);
return true;
}AVL树其他操作
AVL树的最小值
AVLNode* First(AVLNode* ptr)
{
while (ptr != nullptr && ptr->leftchild != nullptr)
{
ptr = ptr->leftchild;
}
return ptr;
}AVL树的最大值
AVLNode* Last(AVLNode* ptr)
{
while (ptr != nullptr && ptr->rightchild != nullptr)
{
ptr = ptr->rightchild;
}
return ptr;
}返回某节点的直接前驱节点
AVLNode* Prev(AVLNode* ptr)
{
if (ptr == nullptr) return nullptr;
if (ptr->leftchild != nullptr)
{
return Last(ptr->leftchild);
}
else
{
AVLNode* pa = ptr->parent;
while (pa != nullptr && pa->rightchild != ptr)
{
ptr = pa;
pa = ptr->parent;
}
return pa;
}
}返回某节点的直接后继节点
AVLNode* Next(AVLNode* ptr)
{
if (ptr == nullptr)return nullptr;
if (ptr->rightchild != nullptr)
{
return First(ptr->rightchild);
}
else
{
AVLNode* pa = ptr->parent;
while (pa != nullptr && pa->leftchild != ptr)
{
ptr = pa;
pa = ptr->parent;
}
return pa;
}
}