C++算法进阶系列之倍增算法 ST 表
1. 引言
前文使用倍增算法实现了快速求幂的运算,本文继续讲解ST表,ST表即倍增表,本质就是动态规划表,记忆化了不同子问题域中的结果,用于实时查询。只是动态规划过程和传统的稍有点不一样,采用了倍增思想。ST表往往用于存储子区间信息,如某区间的最值……
是不是所有的区间问题都可以使用ST表?
某个区间查询问题是否适用ST表,在于其进行的操作是否允许区间重叠。如下图所示:
如求 [1,6]区间的最大值,可以使用如下 2 种方案:
- 直接在
[1,6]子区间内使用求最值算法,找出最值。这个算法较易实现,一个循坏语句就搞定。
- 如果已经知道了区间
[1,5]和区间[3,6]的最大值,这两个区间可认为是区间[1,6]的子区间,且两者有重叠部分,如图可知区间[1,6]最大值是两个子区间中的较大值,即为10。类似于这样的区间关系,是可以使用ST表实现的。
为什么称ST表为倍增表?
整个数组是一个区间,则分割成小区间的方案可以是:
- 长度为
1的区间:[0,0],[1,1],[2,2]…… - 长度为
2的区间:[0,1],[1,2],[2,3]…… - 长度为
3的区间:[0,2],[1,3],[2,4]…… - 长度为
4的区间:[0,3],[1,4],[2,5]…… - 长度为
5的区间……
还可以划分出长度为6、7、8……的区间,如此分肯定是可行的,但是显得过于零碎、过多,维护代价较高。倍增法分割的原则是按长度为 1、2、4、8、16……分割,也就是按 2 的幂次方分割,这便是倍增表的由来。
- 长度为
1的区间:[0,0],[1,1],[2,2]…… - 长度为
2的区间:[0,1],[1,2],[2,3]…… - 长度为
4的区间:[0,3],[1,4],[2,5]…… - 长度为
8的区间:[0,7],[1,8],[2,9]……
为什么说这种方案是可行的?
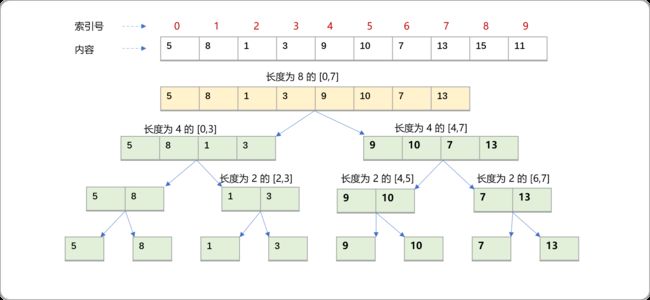
根据前面的分析可知,如果知道当前区间的子区间的最大值且子区间之间连续或重叠的,则当前区间的值可由子区间推导出来。从倍数关系来看,长度为 8 的区间可分割成 2 个长度为 4 的区间,长度为 4 的区间可分割成 2 个长度为 2 的区间……
如下图所示,任何一个区间都可以分割成两个与之有关联的子区间,从而减少更多细碎区间的存在。
2. 生成 ST 表
区间应该有 3 个属性,左端点(left)、右端点(right)、此区间的最大值。以下分别分析长度不同时区间的左端与右端的关系。
先以长度为 8 的区间[0,7]为例探讨左端与右端的关系:
left=0,right=left+23-1=0+8-1=7。
以长度为 4 的区间[4,7]为例探讨左端与右端的关系:
left=4,right=left+22-1=4+4-1=7。
以长度为 2 的区间[4,5]为例探讨左端与右端的关系:
left=4,right=left+21-1=4+2-1=5。
以长度为 1 的区间[4,4]为例探讨左端与右端的关系:
left=4,right=left+01-1=4+1-1=4。
再观察求幂运算中指数的通用性:区间长度为 1 时指数为 0;区间长度为 2 时指数为 1;区间长度为 4 时指数为 2;区间长度为 8 时指数为 3……也就是如果知道了left以及区间长度则可计算出右区间的大小,右区间是动态值。
对于长度为 10的数列而言,到底能划分成多少个不等的区间?
从上述例子来看,数组长度为 10 时,区间最大长度为 8也就是 23 就可以了,其值是 log10(以 2 为底数) 向下取整。有了上述推导的支撑,如可创建 ST就应该呼之欲出了。
创建一个二维数组,命名为 ST表。行坐标表示左端,列坐标并不直接表示右端,而是表示指数,有了指数信息即可以表示区间长度,又能计算出右端大小。如下图 st[0][0]表示的left=0、right=left+20-1=0,即区间[0,0]。
数组存储对应区间的最大值,根据上述的推论可知,区间长度为1的最大值为自己。
当 right=1即表示长度为 2 的区间,此时,如下图 st[0][1]的值应该如何推导出来。
回到上文中的推导理论,知道区间长度为 2 的最大值,可以是它的 2 个长度为 1 的子区间的中的最大值。如下图所示,区间[0,1]的最大值是 max([0,0],[1,1] )的最大值,即为 8。
问题是如何写出动态转移公式?
再分析一下:
- 求指数为
1的区间值,得从指数为0的区间找,首先,指数要降级。 - 左边子区间
[0,0]的left值和区间[0,1]的左值相同,右边子区间[1,1]的左端值是左子区间的left+20=0+1=1。
如此,动态转移公式也就可以出来了:
- 当
right=0时,st[left][right]=nums[left]。 - 当
right!=0时,st[left][right]=max(st[left][right-1],st[left+2right-1][right-1]。
编码实现:
#include
#include
#include
using namespace std;
//st 表
int st[100][10];
//原数组
int nums[100];
//实际长度
int n,col;
/*
* 初始化
*/
void init() {
for(int i=0; i 3. 查询
st表的创建,目的是快速查询某区间的最大值,下面讨论如何准确定位区间,以及找到最大值。
如下图所示,如果用户输入的区间是[0,3],则运气很好,因为恰好有这么一个区间。那么如何得到 st[i][j]中 i和j的值?
显然i=0,求 j的表达式为:i+2j-1=3,则 2j=4-0=4;j=log4(以 2 为底); j=2,也就直接从 st[0][2]得到最大值。
但是,如果输入的区间是[0,6],不存在这么一个区间,则需要从能作为此区间的子区间中查找。
假设在st[i][j]中,i=l,j=p,len=r-l+1(区间长度),找最大的p应满足2p <= len(以l为起点的st表数据覆盖[l,r]中数足够多),则p=int(log(len)/log(2))。
左子区间为 st[l][p],右子区间为 st[x][r]。如何求x,对于st[x][r],应有:[x][x+pow(2,p)-1]<=>[x][r]。所以, x+pow(2,p)-1=r,移项,得:x=r+1-pow(2,p),显然,x>=l ( l+pow(2,p)-1<=r,x+pow(2,p)-1=r,故x>=l)
综上[l,r]的最大值 = max( f[l][p] , f[x][R] )。
完整代码:
#include
#include
#include
using namespace std;
//st 表
int st[100][10];
//原数组
int nums[100];
//实际长度
int n,m,col;
/*
* 初始化
*/
void init() {
for(int i=0; i 测试结果:
4. 总结
区间查询有很多方式,ST是不错的选择。