【考研数学】高等数学第六模块 —— 空间解析几何（2，向量的应用）

---

引言

承接前文，介绍完向量的基本概念与运算后，我们来看看向量有哪些应用。

---

二、向量的应用

2.1 平面

（一）平面的点法式方程

设 $M_0(x_0,y_0,z_0)\in \pi$ ，又有非零向量 $n=\{A,B,C\}\perp \pi$ ，则平面 $\pi$ 的方程为 $$\pi :A(x-x_0)+B(y-y_0)+C(z-z_0)=0.$$ （二）平面的一般式方程

$\pi :Ax+By+Cz+D=0$ ，其中 $n=\{A,B,C\}$ 是平面 $\pi$ 的法向量。

（三）平面的截距式方程

设平面 $\pi$ 与三个坐标轴的交点分别为 $A(a,0,0),B(0,b,0),C(0,0,c)$ ，其中 $a,b,c$ 为非零常数，则平面 $\pi :x/a+y/b+z/c=1.$

（四）平面的三点式方程

设 $A(a_1,b_1,c_1),B(a_2,b_2,c_2),C(a_3,b_3,c_3)$ 为不在一条直线上的三点，则 $A,B,C$ 确定唯一平面 $\pi$ ，平面的法向量为 $n=AB\times BC$ ，再利用点法式方程即可求出平面方程。

2.2 直线

（一）空间直线的一般式方程 $$L:\{\begin{array}{l}{A}_{1}x+B_{1}y+C_{1}z+D_1=0,\\ A_{2}x+B_{2}y+C_{2}z+D_2=0.\end{array}$$ 即写成了两个一般平面的交线形式。

（二）直线的对称式（点向式）方程

对于直线 $L$ ，若有向量 $s=\{m,n,p\}//L$ ，点 $M_0(x_0,y_0,z_0)\in L$ ，则直线 $L$ 的点向式方程为 $$L:\frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{p}.$$ （三）直线的参数式方程

空间直线的参数式方程为 $$L:\{\begin{array}{l}x=x_0+mt,\\ y=y_0+nt,\\ z=z_0+pt,\end{array}$$ 其中，$s=\{m,n,p\}//L,M_0(x_0,y_0,z_0)\in L.$

2.3 特殊曲面

2.3.1 旋转曲面

（一）二维空间旋转曲面

设曲线 $L:f(x,y)=0,z=0$ 为 $xOy$ 平面内的曲线，则曲线 $L$ 绕 $x$ 轴旋转而成的曲面为 ${\sum }_x:f(x,\pm \sqrt{y^2+z^2})=0;$ 曲线 $L$ 绕 $x$ 轴旋转而成的曲面为 ${\sum }_y:f(\pm \sqrt{x^2+z^2},y)=0.$

即绕哪个轴旋转，哪个字母不变，其余字母换成轴字母外其他两个字母的平方和开根号。

（二）三维空间直线旋转曲面

设 $L:\frac{x-a}{m}=\frac{y-b}{n}=\frac{z-c}{p}$ ，其绕 $z$ 轴旋转而成的曲面求法如下：

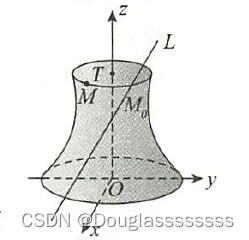
设 $L$ 绕 $z$ 轴旋转而成的曲面为 $\sum$ ，如下图所示。

任取 $M(x,y,z)\in \sum$ ，$M$ 所在的圆位于 $L$ 上的点为 $M_0(x_0,y_0,z)$ ，圆心为 $T(0,0,z)$ 。由于 $|MT|=|M_{0}T|$ ，得 $x^2+y^2=x_0^2+y_0^2$ ，$M_0\in L$ ，代入直线方程，有 $\frac{x_0-a}{m}=\frac{y_0-b}{n}=\frac{z-c}{p}$ ，联立可解得：$x_0=mz/p+a-mc/p,y_0=nz/p+b-nc/p.$ ，于是可得所求曲面方程为 $$\sum :x^2+y^2=(mz/p+a-mc/p{)}^2+(nz/p+b-nc/p{)}^2.$$

关键就是旋转后 $z$ 不变，且到圆心的距离相等，可以联立。

2.3.2 柱面

直线 $L$ 沿着曲线 $C$ 平行移动形成的轨迹叫作柱面，定曲线 $C$ 叫作柱面的准线，动直线 $L$ 叫作柱面的母线。

（一）母线平行于坐标轴的柱面

（二）投影柱面

设 $L:F(x,y,z)=0,G(x,y,z)=0$ 为空间直线，过 $L$ 且平行于 $z$ 轴的柱面方程 $H(x,y)=0$ 即为从 $F(x,y,z)=0,G(x,y,z)=0$ 中消去 $z$ 所得方程。

方程 $f(x,y)=0$ 在二维空间内表示曲线，而在三维空间内表示母线平行于 $z$ 轴的柱面。

2.4 距离

（一）两点之间的距离

设两点 $M_1(x_1,y_1,z_1),M_2(x_2,y_2,z_2)$ ，则这两点之间的距离为 $$d=\sqrt{(x_2-x_1{)}^2+(y_2-y_1{)}^2+(z_2-z_1{)}^2}.$$ （二）点到平面的距离

设点 $M_0(x_0,y_0,z_0)$ ，平面 $\pi :Ax+By+Cz+D=0$ ，则点 $M_0$ 到平面 $\pi$ 的距离为 $$d=\frac{|A{x}_0+B{y}_0+C{z}_0+D|}{\sqrt{A^2+B^2+C^2}}.$$ （三）点到直线的距离

设点 $M_0(x_0,y_0,z_0)$ ，直线 $$L:\frac{x-x_1}{m}=\frac{y-y_1}{n}=\frac{z-z_1}{p}$$ 则点 $M_0$ 到直线 $L$ 的距离为 $$d=\frac{|s\times M_0{M}_1|}{|s|}$$ 其中，$s=\{m,n,p\},M_1(x_1,y_1,z_1)\in L.$

（四）两平行平面之间的距离

平面 ${\pi }_1:Ax+By+Cz+D_1=0$ ，平面 ${\pi }_2:Ax+By+Cz+D_2=0$ ，则平面 ${\pi }_1,{\pi }_2$ 之间的距离为 $$d=\frac{|D_1-D_2|}{\sqrt{A^2+B^2+C^2}}.$$ （五）两空间直线之间的距离

设 $$L_1:\frac{x-x_1}{m_1}=\frac{y-y_1}{n_1}=\frac{z-z_1}{p_1},L_2:\frac{x-x_2}{m_2}=\frac{y-y_2}{n_2}=\frac{z-z_2}{p_2}$$ 为两条直线，$s_1=\{m_1,n_1,p_1\},s_2=\{m_2,n_2,p_2\}$ 分别为 $L_1,L_2$ 的方向向量，$M_1(x_1,y_1,z_1)\in L_1,M_2(x_2,y_2,z_2)\in L_2$ ，则 $L_1,L_2$ 的位置关系如下：

1. 当 $(s_1\times s_2)\cdot M_1{M}_2=0$ 时，$L_1,L_2$ 共面；
2. 当 $(s_1\times s_2)\cdot M_1{M}_2\ne 0$ 时，$L_1,L_2$ 异面，它们之间的距离为 $$d=\frac{(s_1\times s_2)\cdot M_1{M}_2}{|s_1\times s_2|}.$$

2.5 夹角

（一）两向量之间的夹角

设 $\alpha ,\beta$ 为两个向量，则 $\alpha ,\beta$ 之间的夹角为 $$\theta =\arccos \frac{\alpha \cdot \beta }{|\alpha ||\beta |}.$$ （二）两直线之间的夹角

设 $$L_1:\frac{x-x_1}{m_1}=\frac{y-y_1}{n_1}=\frac{z-z_1}{p_1},L_2:\frac{x-x_2}{m_2}=\frac{y-y_2}{n_2}=\frac{z-z_2}{p_2}$$ 为两条直线，$s_1=\{m_1,n_1,p_1\},s_2=\{m_2,n_2,p_2\}$ 分别为 $L_1,L_2$ 的方向向量，则它们之间的夹角为 $$\theta =\arccos \frac{s_1\cdot s_2}{|s_1||s_2|}.$$ （三）两平面之间的夹角

平面 ${\pi }_1:A_{1}x+B_{1}y+C_{1}z+D_1=0$ ，平面 ${\pi }_2:A_{2}x+B_{2}y+C_{2}z+D_2=0$ ，$n_1=\{A_1,B_1,C_1\},n_2=\{A_2,B_2,C_2\}$ 分别为 ${\pi }_1,{\pi }_2$ 的法向量，则平面 ${\pi }_1,{\pi }_2$ 之间的夹角为 $$\theta =\arccos \frac{n_1\cdot n_2}{|n_1||n_2|}.$$ （四）直线与平面之间的夹角

设平面 $\pi :Ax+By+Cz+D=0$ 和直线 $$L:\frac{x-x_1}{m}=\frac{y-y_1}{n}=\frac{z-z_1}{p}$$ $n=\{A,B,C\},s=\{m,n,p\}$ 分别为平面的法向量和直线的方向向量，则直线 $L$ 和平面 $\pi$ 之间的夹角为 $$\theta =\arcsin \frac{n\cdot s}{|n||s|}.$$

---

写在最后

公式好多，好容易记混掉，不过也算蛮有规律的，拿到此，空间解析几何的理论部分就结束了，主要是围绕向量做文章。