Atcoder做题记录

ARC101E - Ribbons on Tree

好菜啊，不会做。。。
容斥树形$dp$，设$f[x][k]$为以$x$为根的子树，上面大小为$k$的连通块没有匹配。
首先一个大小为$n$的子树的自由完全匹配方案我们先预处理出来。
转移的话对于一个$x$考虑那些边是一定不选的的，不选的边的边数为$T$的话，容斥系数为$-1^{|T|}$
对于一个$x$的子节点$y$，
那么就是分两种转移，一种是当前这条边选择，那么直接合并两个块。
如果不选择，那就是$y$这个子树中自由完全匹配。

---

ARC100E - Or Plus Max

做一个类似与快速莫比乌斯变换的过程，对每个$i$取一个最大值和一个次大值相加即可。

---

ARC100F - Colorful Sequences

好菜啊，不会做。。。
考虑用总包含$m$这个序列的方案数减去不合法的。
总方案数首先是：$(n-m+1)k^{n-m}$
然后分情况讨论。
对于这个序列本身就是一个合法的序列，那么不合法的方案数为$0$。
对于这个序列是一个每个元素互不相同的序列，考虑$dp$。
设$f[i][j]$为长度为$i$的序列后面$j$个数各不相同，下一个数就会出现重复，$dp$过程中保证$j<m$即可。
转移就是讨论新加入的这个元素是全新的还是跟前面出现重复的。
对于剩下的情况，那么就是只用考虑前面的一段和后面的一段即可。
改一下初始值，跟上面做个类似的$dp$。

---

ARC099E - Independence

口胡一下。
大概就是在补图上跑个二分图染色再做一下背包就好了。

---

ARC099F - Independence

可以$Hash$来做。
每次在$S$前面加入一个字符，相当于：
$+$：$Hash$值加$1$
$-$：$Hash$值减$1$
$>$：$Hash$值乘上一个$Base$
$<$：$Hash$值除上一个$Base$
然后就可以用个$map$来搞搞了。

---

Tenka1 Programmer Contest 2019

D

你可以考虑用不合法的减去合法的。
那就是相当于，如果$C$为最大的集合，$A+B-C<=0$。
你就可以直接设一维为$A+B-C$，然后就可以直接$dp$了。

E

首先所有$a_i$的公因数可以成为答案。
然后$f(i)\equiv 0(modp)$，那么该多项式肯定满足存在一个因子$(x-i)$。
那么就相当于要满足存在因子${\prod }_{i=0}^{p-1}(x-i)\equiv (x^p-x)(modp)$
你可以发现答案肯定在$N$以内，直接暴力枚举判就好了。

F

考虑枚举$0$的个数。
设和为$S$，有三种情况。
$1.S\le X$
$2.(S-X)$为奇数，序列仅有$2$。
$3.(S-X)$为奇数，任意一个$1$，左边的和加上$1$不超过$X$，右边的和加上$1$不超过$X$。
然后你枚举一下$S$，搞一搞就好了。

---

ARC097E - Sorted and Sorted

设$dp[i][j]$为已选了$i$个白色，和$j$个黑色。
设$w[i][j]$为第$i$个白色后面有多少个$1$~$i$中的白色，有多少个$1$ ~ $j$中的黑色，$b[i][j]$同理。
那么转移就是$f[i][j]=min(f[i-1][j]+w[i][j],f[i][j-1]+b[i][j])$

---

ARC094E - Tozan and Gezan

设满足$A_i>B_i$的点的最小值为$C$。
直接输出${\sum }_{i=1}^n{B}_i-C$即可，挺显然的。

---

ARC094F - Normalization

打了个表发现，对于长度大于三的有规律，
对于一个串$S$他能变换到的串$T$满足：
$1.T$的$sum$和$S$的$sum$在模$3$意义下同余。
$2.T$至少有一对相邻的数是相同的，或者是这个串本身。
搞一个$dp$就完事了。
证明的话，可以用归纳？？？

---

AGC005E - Sugigma: The Showdown

好菜啊，并不会做。。。
有一个结论是$A$选手假设走到了红树的一条边$(x,y)$在蓝树上满足$dis(x,y)>2$，那么答案就是$-1$。
假设以$B$选手的起始位置为根建出一颗蓝树，可以发现，$A$选手的走法肯定是一直往下跑，然后跑到一个位置后原地等死。
那么就可以找出$A$选手能往下拓展并且不被$B$抓到的最深的深度，就是答案了。
然后跑两个$dfs$就行了。

---

AGC005F - Many Easy Problems

考虑一个点$x$对某一个$k$的贡献。
容斥一下可得：
$$C_n^k-\sum _{fa[y]=x}{C}_{tot[y]}^k-C_{n-tot[x]}^k$$
就可以$NTT$了。

---

AGC032

B

我的做法是乱搞的。
就是你把点的和搞一个最小的约数，以这个约数作为块数，就A了。

C

一开始以为是找到任意三个环，但实际上是问你整个图能不能分成三个环。
那么，首先如果有某个点的度数是奇数，肯定就是不行的。
然后如果有点的个数大于等于六，就一定OK。
否则，如果有三个及以上的四度数的点，也OK。
如果只有两个呢？
可能是不行的，唯一的一种情况就是：

判一下就好了。

D

我是这么想的，就是每个点其实最多只会移一次，某些点可能是不会动的。
那么我们可以考虑设这样的状态：$dp[i][j]$当且$dp$到第$i$位，编号为j的作为最后一个不动的点，那么就可以得到这样的转移：
$dp[i][j]=min(dp[i][j],f[i-1][j]+A),dp[i][a[i]]=min(dp[i][a[i]],dp[i-1][j]),a[i]>j$
分别表示继续以j为不动，那么$a[i]$往右移，以$a[i]$为不动，则不需要新的移动。
$dp[i][j]=min(dp[i][j],dp[i-1][j]+B),a[i]<j$
这种情况下，$a[i]$无法作为不动，只能往左移。

E

首先就是说可以找到一个分界点$mid$使得$(1-mid,2-mid-1...)$配对，且每一组配对和小于$M$，大于等于的部分也是头尾配对。
我觉得题解的图挺好的，搬来，其中蓝色线表示小于$M$的配对，红色则为大于等于$M$的配对。

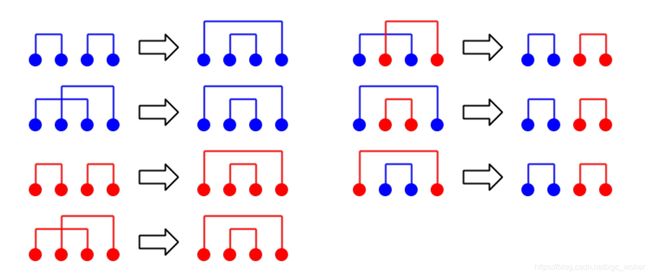
F

这道题挺有意思的。
首先随便切一刀红色的边，然后再顺$120$度切一个绿的边，然后再逆$120$度切一个蓝色的。
然后最小的角就是距离最小的颜色不相同相邻直线，令第一次划分为0，则也相当于求$\lfloor 0,1/3)$距离最小的颜色不相同相邻直线，除去第一次划分，一共有$n-1$个点，把这个角分成了$n$块。
考虑求一个$f(i)$表示分成$i$个颜色块的方案数，这个可以递推。
然后考虑求出分成$i$段的期望最小段$g(i)$，分成$i$段的期望长度是$\frac{i}{3n}$。
$g(i)=\frac{i}{3n}{\int }_{t=0}^{\frac{1}{i}}P(min>=t)dt=\frac{i}{3n}{\int }_{t=0}^{\frac{1}{i}}(1-it{)}^{i-1}dt=\frac{i}{3n}{\int }_{t=0}^1\frac{t^{i-1}}{i}dt=\frac{1}{3ni}$
答案就等于${\sum }_{i=1}^{n}f(i)g(i)$

---