2022年蓝桥杯C++B组(超详解)
文章目录
-
- A 九进制转十进制
- B 顺子日期
- C 刷题统计
- D 修剪灌木
- E X进制减法
- F 统计子矩阵
- G 积木画
- H 扫雷
- I 李白打酒加强版
- J 砍竹子
A 九进制转十进制
问题描述:
九进制正整数 ( 2022 ) 9 (2022)_9 (2022)9转换成十进制等于多少?
思路:
请类比二进制转换成十进制:
( 11010 ) 2 = 1 × 2 4 + 1 × 2 3 + 0 × 2 2 + 1 × 2 1 + 0 × 2 0 = ( 26 ) 10 (11010)_2 = 1×2^4 + 1×2^3 + 0×2^2 + 1×2^1 + 0×2^0 = (26)_{10} (11010)2=1×24+1×23+0×22+1×21+0×20=(26)10
C++代码
#include 输出:
1478
B 顺子日期
题目描述:
小明特别喜欢顺子。顺子指的就是连续的三个数字:123、456等。顺子日期指的就是在日期的yyyymmdd表示法中,存在任意连续的三位数是一个顺子的日期。例如20220123就是一个顺子日期,因为它出现了一个顺子:123;而20221023则不是一个顺子日期,它一个顺子也没有。小明想知道在整个2022年份中,一共有多少个顺子日期。
思路:
直接硬模拟打暴力即可!
C++代码
#include 输出:
20220120
20220121
20220122
20220123
20220124
20220125
20220126
20220127
20220128
20220129
20221012
20221123
20221230
20221231
14
C 刷题统计
问题描述:
小明决定从下周一开始努力刷题准备蓝桥杯竞赛。他计划周一至周五每天做 a a a 道题目,周六和周日每天做 b b b 道题目。请你帮小明计算,按照计划他将在第几天实现做题数大于等于 n n n 题?
输入格式:
输入一行包含三个整数 a , b a, b a,b 和 n n n。
输出格式:
输出一个整数代表天数。
输入样例:
10 20 99
输出样例:
8
提示:
对于 50 50% 50 的评测用例, 1 ≤ a , b , n ≤ 1 0 6 1 ≤ a, b, n ≤ 10^6 1≤a,b,n≤106 . 对于 100 100% 100 的评测用例, 1 ≤ a , b , n ≤ 1 0 18 1 ≤ a, b, n ≤ 10^{18} 1≤a,b,n≤1018 。
思路:
每个星期的刷题量都是 5 × a + 2 × b 5 \times a + 2 \times b 5×a+2×b,我们可以先求出需要多少星期,最后余下来的直接模拟即可!时间复杂度: O ( 1 ) O(1) O(1)。
C++代码:
#include D 修剪灌木
题目描述:
爱丽丝要完成一项修剪灌木的工作。有 N N N 棵灌木整齐的从左到右排成一排。爱丽丝在每天傍晚会修剪一棵灌木,让灌木的高度变为 0 0 0 厘米。爱丽丝修剪灌木的顺序是从最左侧的灌木开始,每天向右修剪一棵灌木。当修剪了最右侧的灌木后,她会调转方向,下一天开始向左修剪灌木。直到修剪了最左的灌木后再次调转方向。然后如此循环往复。灌木每天从早上到傍晚会长高 1 1 1 厘米,而其余时间不会长高。在第一天的早晨,所有灌木的高度都是 0 0 0 厘米。爱丽丝想知道每棵灌木最高长到多高。
输入格式:
一个正整数 N N N ,含义如题面所述。
输出格式:
输出 N N N 行,每行一个整数,第i行表示从左到右第 i i i 棵树最高能长到多高。
样例输入:
3
样例输出:
4
2
4
提示:
对于 30 30% 30 的数据, N ≤ 10 N ≤ 10 N≤10。 对于 100 100% 100 的数据, 1 < N ≤ 10000 1 < N ≤ 10000 1<N≤10000。
思路:
模拟一下示例:
对于一颗灌木来说,当爱丽丝从该灌木到离该灌木最远的终点的一个来回是,是该灌木能够长的最高的时候,即对于一个 1 ∼ n 1\sim n 1∼n 的灌木来说,第 i i i 个灌木最高高度为 2 × m a x ( n − i , i − 1 ) 2 \times max(n - i, i - 1) 2×max(n−i,i−1) 。
C++代码:
#include E X进制减法
题目描述:
进制规定了数字在数位上逢几进一。
X X X 进制是一种很神奇的进制,因为其每一数位的进制并不固定!例如说某种 X X X 进制数,最低数位为二进制,第二数位为十进制,第三数位为八进制,则 X X X 进制数 321 转换为十进制数为 65。
现在有两个 X X X 进制表示的整数 A A A 和 B B B,但是其具体每一数位的进制还不确定,只知道 A A A 和 B B B 是同一进制规则,且每一数位最高为 N N N 进制,最低为二进制。请你算出 A − B A-B A−B 的结果最小可能是多少。
请注意,你需要保证 A A A 和 B B B 在 X X X 进制下都是合法的, 即每一数位上的数字要小于其进制。
输入格式:
第一行一个正整数 N N N,含义如题面所述。
第二行一个正整数 M a M_{a} Ma,表示 X X X 进制数 A A A 的位数。
第三行 M a M_{a} Ma 个用空格分开的整数,表示 X X X 进制数 A A A 按从高位到低位顺序各个数位上的数字在十进制下的表示。
第四行一个正整数 M b M_{b} Mb,表示 X X X 进制数 B B B 的位数。
第五行 M b M_{b} Mb 个用空格分开的整数,表示 X X X 进制数 B B B 按从高位到低位顺序各个数位上的数字在十进制下的表示。
请注意,输入中的所有数字都是十进制的。
输出格式:
输出一行一个整数,表示 X X X 进制数 A − B A-B A−B 的结果的最小可能值转换为十进制后再模 1000000007 1000000007 1000000007(即 1 0 9 + 7 10^9+7 109+7)的结果。
样例输入:
11
3
10 4 0
3
1 2 0
样例输出:
94
提示:
【样例说明】
当进制为:最低位 2 2 2 进制, 第二数位 5 5 5 进制, 第三数位 11 11 11 进制时, 减法得到的差最小。此时 A A A 在十进制下是 108 108 108, B B B 在十进制下是 14 14 14,差值是 94 94 94。
【评测用例规模与约定】
对于 30 % 30 \% 30% 的数据, N ≤ 10 , M a , M b ≤ 8 N \leq 10,M_{a}, M_{b} \leq 8 N≤10,Ma,Mb≤8.
对于 100 % 100 \% 100% 的数据, 2 ≤ N ≤ 1000 , 1 ≤ M a , M b ≤ 1 0 5 , A ≥ B 2 \leq N \leq 1000,1 \leq M_{a}, M_{b} \leq 10^5,A \geq B 2≤N≤1000,1≤Ma,Mb≤105,A≥B。
思路:
对于题目中给的数 321 321 321 来说, 3 3 3 所在的位是 $8 $进制, 2 2 2 所在的位是 10 10 10 进制, 1 1 1 所在的位是 2 2 2 进制。
我们可以发现:
3 × 10 × 2 + 2 × 1 + 1 = 65 3 \times 10 \times 2+2 \times 1+1=65 3×10×2+2×1+1=65
因此,我们可以得到:第 i i i 位的权值 == 比第 i i i 位低的位上的进制之积,即 w i = ∏ j = 0 i a j w_i=\prod_{j=0}^ia_j wi=∏j=0iaj 。
设 a i , b i a_i,b_i ai,bi 为 A , B A,B A,B 的第 i i i 位,那么 A − B A - B A−B 的第 i i i 为 w a i × a i − w b i × b i w_{a_i} \times a_i - w_{b_i} \times b_i wai×ai−wbi×bi ,由于 A A A 和 B B B 是同一进制规则,可以知道 w a i = w b i = C w_{a_i}=w_{b_i}=C wai=wbi=C,即 A − B A - B A−B 的第 i i i 为 C ( a i − b i ) C(a_i-b_i) C(ai−bi),若想使得 C ( a i − b i ) C(a_i-b_i) C(ai−bi) 最小, a i − b i a_i-b_i ai−bi 是固定的,那么可以使得 C C C 最小即可! C = ∏ j = 0 i a j C=\prod_{j=0}^ia_j C=∏j=0iaj,可以知道我们要使得每一位的进制是最小的,即 m a x ( a i , b i ) + 1 max(a_i, b_i) + 1 max(ai,bi)+1。
C++代码:
#include F 统计子矩阵
题目描述:
给定一个 N × M N \times M N×M 的矩阵 A A A,请你统计有多少个子矩阵 (最小 1 × 1 1 \times 1 1×1, 最大 N × M ) N \times M) N×M) 满足子矩阵中所有数的和不超过给定的整数 K K K。
输入格式:
第一行包含三个整数 N , M N, M N,M 和 K K K。
之后 N N N 行每行包含 M M M 个整数, 代表矩阵 A A A。
输出格式:
一个整数代表答案。
样例输入:
3 4 10
1 2 3 4
5 6 7 8
9 10 11 12
样例输出:
19
提示:
【样例说明】
满足条件的子矩阵一共有 19 19 19,包含:
大小为 1 × 1 1 \times 1 1×1 的有 10 10 10 个。
大小为 1 × 2 1 \times 2 1×2 的有 3 3 3 个。 大小为 1 × 3 1 \times 3 1×3 的有 2 2 2 个。
大小为 1 × 4 1 \times 4 1×4 的有 1 1 1 个。
大小为 2 × 1 2 \times 1 2×1 的有 3 3 3 个。
【评测用例规模与约定】
对于 30 % 30 \% 30% 的数据, N , M ≤ 20 N, M \leq 20 N,M≤20.
对于 70 % 70 \% 70% 的数据, N , M ≤ 100 N, M \leq 100 N,M≤100.
对于 100 % 100 \% 100% 的数据, 1 ≤ N , M ≤ 500 , 0 ≤ A i j ≤ 1000 , 1 ≤ K ≤ 2.5 × 1 0 8 1 \leq N, M \leq 500,0 \leq A_{i j} \leq 1000,1 \leq K \leq 2.5\times10^8 1≤N,M≤500,0≤Aij≤1000,1≤K≤2.5×108.
思路:
参考
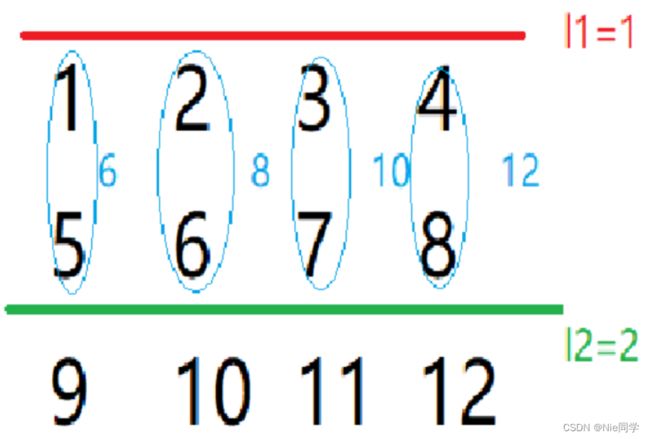
我们可以假想有水平的两条横线,切出了中间一块区域。用 O ( n 2 ) O(n^2) O(n2) 的时间,枚举这两条横线(如下图所示)。
枚举出两条横线之后,就可以把中间的每一列数给当成一个整体,例如上图 l 1 = 1 , l 2 = 2 l1=1,l2=2 l1=1,l2=2 的情况下,就可以把矩阵视为一个序列 [ 6 , 8 , 10 , 12 ] [6,8,10,12] [6,8,10,12] 。
我们只需要求出在这个序列中,有几个子序列的元素之和小于等于 k k k 即可。这就把二维问题转化为了一维问题。
那么现在我们还有 O ( m ) O(m) O(m) 的时间来处理子序列的问题。考虑有两个指针 l l l 和 r r r,代表子序列的左端点与右端点。注意到矩阵中所有的元素都是正数,那么显然有下面两个结论:
- 若 sum ( l , r ) ≤ k \operatorname{sum}(l, r) \leq k sum(l,r)≤k ,且 l + 1 ≤ r l+1 \leq r l+1≤r ,则 sum ( l + 1 , r ) ≤ k \operatorname{sum}(l+1, r) \leq k sum(l+1,r)≤k 。
- 若 sum ( l , r ) > k \operatorname{sum}(l, r)>k sum(l,r)>k ,且 r + 1 ≤ n r+1 \leq n r+1≤n ,则 sum ( l , r + 1 ) > k \operatorname{sum}(l, r+1)>k sum(l,r+1)>k 。
在遍历 r r r 时,如果当前的子序列元素和小于等于 k k k ,那么就有 r − l + 1 r-l+1 r−l+1 个新答案。如果大于 k k k了,就考虑向右移动 , l l l使得最终的子序列元素和仍然小于等于 k k k。
为什么有 r − l + 1 r-l+1 r−l+1个新答案?
右指针从 r − 1 r-1 r−1 移动到 r r r 处,那么新增的矩阵数为: [ r ] , [ r − 1 , r ] , [ r − 2 , r ] , [ r − 3 , r ] . . . [ l , r ] [r],[r-1,r],[r-2,r],[r-3,r]...[l,r] [r],[r−1,r],[r−2,r],[r−3,r]...[l,r],共计 r − l + 1 r - l+1 r−l+1 条。
举个例子:有一个序列 [ 1 , 3 , 4 , 3 ] [1,3,4,3] [1,3,4,3] ,试求出其中有多少个子序列,满足该子序列的所有元素之和小于等于 10 10 10。
- l = 1 , r = 1 l=1, r=1 l=1,r=1, sum = 1 =1 =1, a n s = 0 + ( 1 − 1 + 1 ) = 1 ans=0+(1-1+1)=1 ans=0+(1−1+1)=1
- l = 1 , r = 2 l=1, r=2 l=1,r=2, s u m = 4 sum=4 sum=4, a n s = 1 + ( 2 − 1 + 1 ) = 3 ans=1+(2-1+1)=3 ans=1+(2−1+1)=3
批注:因为 l = 1 , r = 2 l=1,r=2 l=1,r=2 都可以,那么 l = 2 , r = 2 l=2,r=2 l=2,r=2 肯定可以。
- l = 1 , r = 3 l=1, r=3 l=1,r=3, s u m = 8 sum=8 sum=8, a n s = 3 + ( 3 − 1 + 1 ) = 6 ans=3+(3-1+1)=6 ans=3+(3−1+1)=6
- l = 1 , r = 4 l=1, r=4 l=1,r=4, s u m = 11 sum=11 sum=11
批注:此时考虑移动 l l l 使得 s u m ≤ k sum \leq k sum≤k。 只需要向右移动一格 l l l 就行了。
- l = 2 , r = 4 , s u m = 8 , a n s = 6 + ( 4 − 2 + 1 ) = 9 l=2,r=4,sum=8,ans=6+(4-2+1)=9 l=2,r=4,sum=8,ans=6+(4−2+1)=9
此时 r = 4 r=4 r=4,且有解了,停止循环。
C++代码:
#include G 积木画
题目描述:
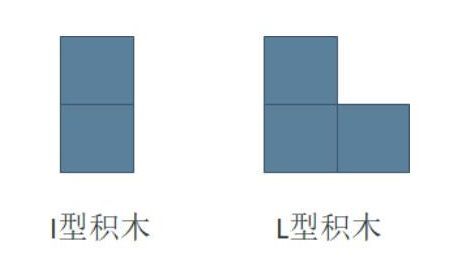
小明最近迷上了积木画,有这么两种类型的积木,分别为 I I I 型(大小为 2 2 2 个单位面积) 和 L L L 型 (大小为 3 3 3 个单位面积):
同时,小明有一块面积大小为 2 × N 2 \times N 2×N 的画布,画布由 2 × N 2 \times N 2×N 个 1 × 1 1 \times 1 1×1 区域构成。小明需要用以上两种积木将画布拼满,他想知道总共有多少种不同的方式? 积木可以任意旋转,且画布的方向固定。
输入格式:
输入一个整数 N N N,表示画布大小。
输出格式:
输出一个整数表示答案。由于答案可能很大,所以输出其对 1000000007 1000000007 1000000007(即 1 0 9 + 7 10^9+7 109+7)取模后的值。
样例输入:
3
样例输出:
5
提示:
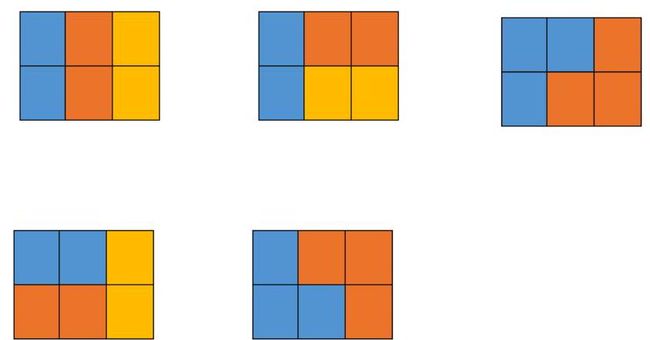
【样例说明】
【评测用例规模与约定】
对于所有测试用例, 1 ≤ N ≤ 1 0 7 1 \leq N \leq 10^7 1≤N≤107。
思路:
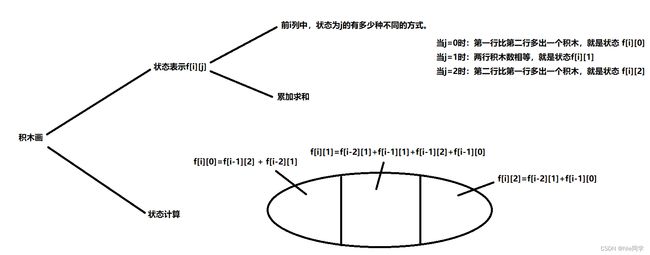
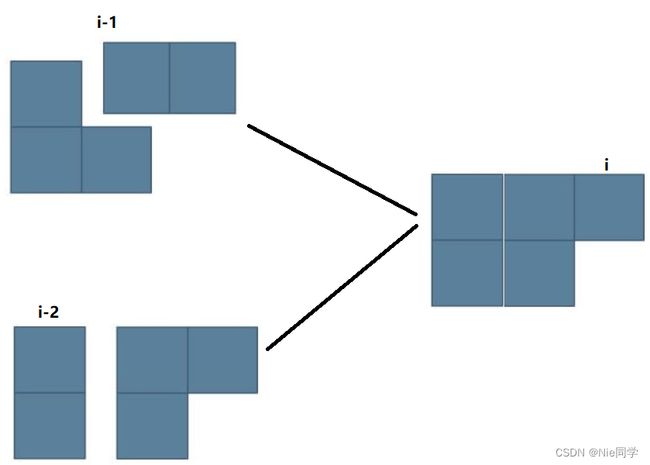
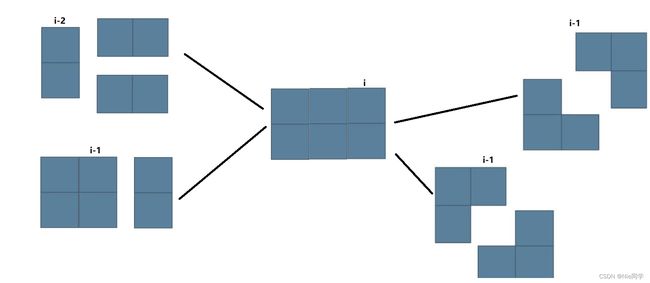
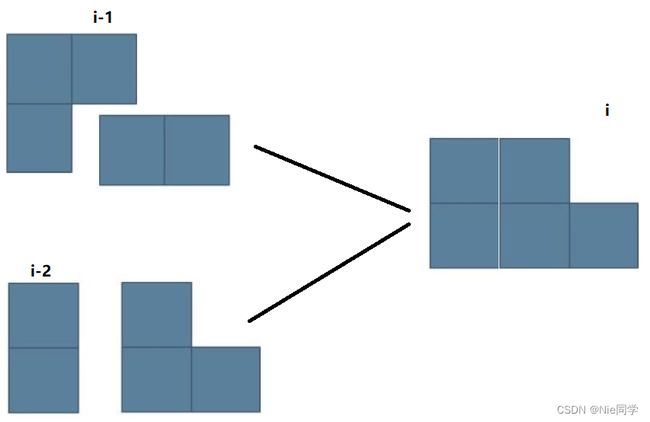
- 第一行比第二行多出一个积木,也就是状态
f[i][0]。此时我们可以用一个 I 型积木在第一行横向填补,这样在填补前第二行就会多出一个积木,也就是f[i-1][2];也可以用一个 L 型积木填补第 i i i 列和 i − 1 i-1 i−1 列,这样填补前两行积木数就相等,也就是f[i-2][1]。
- 两行积木数相等,即状态
f[i][1]。此时有 4 4 4 种情况。我们可以用两个 I 型积木横向填补第 i i i列和第 i − 1 i-1 i−1 列,就是f[i-2][1];可以用一个 I 型积木纵向填补第 i i i 列,也就是f[i-1][1];可以用一个 L 型积木填补第 i i i 列和第 i − 1 i-1 i−1 列的第一行,也就是f[i-1][2];还可以用一个 L 型积木填补第 i i i 列和第 i − 1 i-1 i−1 列的第二行,也就是f[i-1][0]。
- 第二行比第一行多出一个积木,也就是状态
f[i][2]。此时与上一种情况类似,也是两种方案,分别是用一个 I 型积木在第二行横向填补和用一个 L 型积木进行填补。分别是f[i-1][0]和f[i-2][1]。
C++代码:
#include H 扫雷
题目描述:
小明最近迷上了一款名为《扫雷》的游戏。其中有一个关卡的任务如下,在一个二维平面上放置着 n n n 个炸雷,第 i i i 个炸雷 ( x i , y i , r i ) \left(x_{i}, y_{i}, r_{i}\right) (xi,yi,ri) 表示在坐标 ( x i , y i ) \left(x_{i}, y_{i}\right) (xi,yi) 处存在一个炸雷,它的爆炸范围是以半径为 r i r_{i} ri 的一个圆。
为了顺利通过这片土地,需要玩家进行排雷。玩家可以发射 m m m 个排雷火箭,小明已经规划好了每个排雷火箭的发射方向,第 j j j 个排雷火箭 ( x j , y j , r j ) \left(x_{j}, y_{j}, r_{j}\right) (xj,yj,rj) 表示这个排雷火箭将会在 ( x j , y j ) \left(x_{j}, y_{j}\right) (xj,yj) 处爆炸,它的爆炸范围是以半径为 r j r_{j} rj 的一个圆,在其爆炸范围内的炸雷会被引爆。同时,当炸雷被引爆时,在其爆炸范围内的炸雷也会被引爆。现在小明想知道他这次共引爆了几颗炸雷?
你可以把炸雷和排雷火箭都视为平面上的一个点。一个点处可以存在多个炸雷和排雷火箭。当炸雷位于爆炸范围的边界上时也会被引爆。
输入格式:
输入的第一行包含两个整数 n n n、 m m m。
接下来的 n n n 行, 每行三个整数 x i , y i , r i x_{i}, y_{i}, r_{i} xi,yi,ri, 表示一个炸雷的信息。
再接下来的 m m m 行,每行三个整数 x j , y j , r j x_{j}, y_{j}, r_{j} xj,yj,rj, 表示一个排雷火箭的信息。
输出格式:
输出一个整数表示答案。
样例输入:
2 1
2 2 4
4 4 2
0 0 5
样例输出:
2
提示:
【样例说明】
示例图如下, 排雷火箭 1 覆盖了炸雷 1 , 所以炸雷 1 被排除; 炸雷 1 又覆 盖了炸雷 2 , 所以炸雷 2 也被排除。
【评测用例规模与约定】
对于 40 % 40 \% 40% 的评测用例: 0 ≤ x , y ≤ 1 0 9 , 0 ≤ n , m ≤ 1 0 3 , 1 ≤ r ≤ 10 0 \leq x, y \leq 10^{9}, 0 \leq n, m \leq 10^{3}, 1 \leq r \leq 10 0≤x,y≤109,0≤n,m≤103,1≤r≤10.
对于 100 % 100 \% 100% 的评测用例: 0 ≤ x , y ≤ 1 0 9 , 0 ≤ n , m ≤ 5 × 1 0 4 , 1 ≤ r ≤ 10 0 \leq x, y \leq 10^{9}, 0 \leq n, m \leq 5 \times 10^{4}, 1 \leq r \leq 10 0≤x,y≤109,0≤n,m≤5×104,1≤r≤10.
思路:
如果直接枚举每个地雷和所有地雷的情况,时间复杂度为 n 2 n^2 n2,会超时。
由题目可知, r ≤ 10 r \leq 10 r≤10,那么我们对每个地雷只需要遍历周围一圈 r r r 即可。
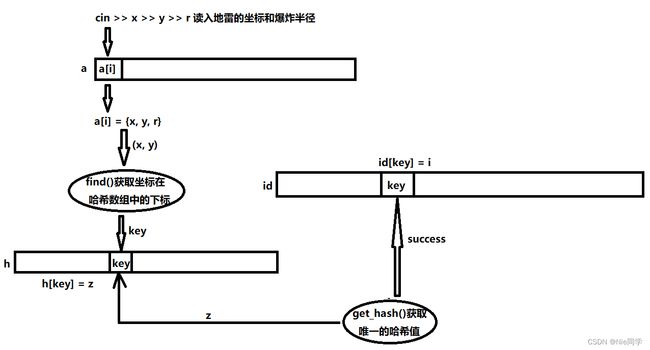
由于这样是遍历每个坐标点,而且一共有 5 × 1 0 4 5 \times 10^4 5×104 个地雷,但是它的坐标范围在 [ 0 , 1 0 9 ] [0, 10^9] [0,109],我们需要通过手写散列表来实现离散化的效果。
那么如何去保证我们求得的哈希值是唯一的呢?
h a s h v a l u e = x × 1 0 9 + y hash_{value} = x \times 10^9 + y hashvalue=x×109+y,因为 0 ≤ x , y ≤ 1 0 9 0≤x,y≤10^9 0≤x,y≤109 故这样的运算可以使得高9位是 x x x 的坐标,低9位是 y y y 的坐标,而我们总是保留坐标相同且爆炸半径最大的那个点,所以保证了 x , y x,y x,y 的唯一性,故这样算出来的哈希值一定是唯一的!
C++代码:
#include I 李白打酒加强版
题目描述:
话说大诗人李白,一生好饮。幸好他从不开车。
一天,他提着酒壶,从家里出来,酒壶中有酒 2 2 2 斗。他边走边唱:
无事街上走,提壶去打酒。
逢店加一倍,遇花喝一斗。
这一路上,他一共遇到店 N N N 次,遇到花 M M M 次。已知最后一次遇到的是花,他正好把酒喝光了。
请你计算李白这一路遇到店和花的顺序,有多少种不同的可能?
注意:壶里没酒( 0 0 0 斗)时遇店是合法的,加倍后还是没酒;但是没酒时遇花是不合法的。
输入格式:
第一行包含两个整数 N N N 和 M M M。
输出格式:
输出一个整数表示答案。由于答案可能很大,输出模 1000000007 1000000007 1000000007(即 1 0 9 + 7 10^9+7 109+7)的结果。
样例输入:
5 10
样例输出:
14
提示:
【样例说明】
如果我们用 0 代表遇到花,1 代表遇到店, 14 14 14 种顺序如下:
010101101000000
010110010010000
011000110010000
100010110010000
011001000110000
100011000110000
100100010110000
010110100000100
011001001000100
100011001000100
100100011000100
011010000010100
100100100010100
101000001010100
【评测用例规模与约定】
对于 40 % 40 \% 40% 的评测用例: 1 ≤ N , M ≤ 10 1 \leq N, M \leq 10 1≤N,M≤10。
对于 100 % 100 \% 100% 的评测用例: 1 ≤ N , M ≤ 100 1 \leq N, M \leq 100 1≤N,M≤100。
思路:
参考
采用动态规划的策略:
初始化操作:当经过 0 0 0 次店, 0 0 0 次花的时候,且李白酒壶里的酒还剩 2 2 2 斗时,即 f [ 0 ] [ 0 ] [ 2 ] = 1 f[0][0][2] = 1 f[0][0][2]=1 ,共有一种情况,当然当经过 0 0 0 次店, 0 0 0 次花的时候,且李白酒壶里的酒不是 2 2 2 斗时,显然时不可能的,即 f [ 0 ] [ 0 ] [ k ] = 0 f[0][0][k]=0 f[0][0][k]=0。
我们可以粗略的估算一下 k k k 的范围,因为题目中已知最后一次遇到的是花,他正好把酒喝光了,且逢店加一倍,遇花喝一斗。
可以得出以下式子: 2 × N = M 2 \times N = M 2×N=M,故 k k k 的最大值为 M M M ,体重 1 ≤ M ≤ 100 1 \leq M \leq100 1≤M≤100,故 1 ≤ N , M , k ≤ 100 1≤N,M,k≤100 1≤N,M,k≤100。
最后打印答案的时候不是打印 f [ n ] [ m ] [ 0 ] f[n][m][0] f[n][m][0] ,因为这么打印是无法区分最后是到花还是到店,我们可以往前推一步,如果最后到花,那么喝完的上一步应该是 f [ n − 1 ] [ m ] [ 1 ] f[n - 1][m][1] f[n−1][m][1],所以最后答案是 f [ n − 1 ] [ m ] [ 1 ] f[n - 1][m][1] f[n−1][m][1]。
C++代码:
#include J 砍竹子
题目描述:
这天,小明在砍竹子,他面前有 n n n 棵竹子排成一排,一开始第 i i i 棵竹子的高度为 h i h_{i} hi.
他觉得一棵一棵砍太慢了,决定使用魔法来砍竹子。魔法可以对连续的一段相同高度的竹子使用,假设这一段竹子的高度为 H H H,那么使用一次魔法可以把这一段竹子的高度都变为 ⌊ ⌊ H 2 ⌋ + 1 ⌋ \left\lfloor\sqrt{\left\lfloor\frac{H}{2}\right\rfloor+1}\right\rfloor ⌊⌊2H⌋+1⌋, 其中 ⌊ x ⌋ \lfloor x\rfloor ⌊x⌋ 表示对 x x x 向下取整。小明想知道他最少使用多少次魔法可以让所有的竹子的高度都变为 1 1 1。
输入格式:
第一行为一个正整数 n n n,表示竹子的棵数。
第二行共 n n n 个空格分开的正整数 h i h_{i} hi,表示每棵竹子的高度。
输出格式:
一个整数表示答案。
样例输入:
6
2 1 4 2 6 7
样例输出
5
提示:
【样例说明】
其中一种方案:
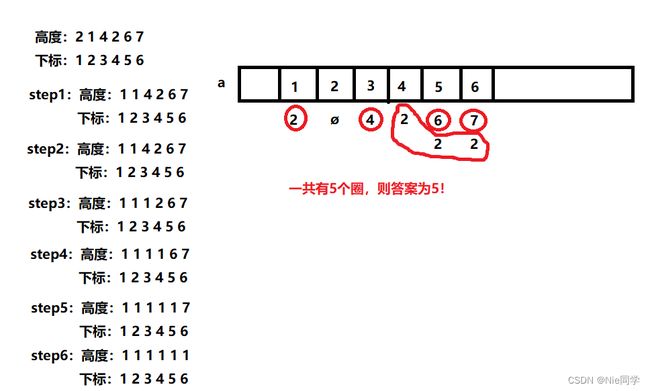
214267 → 214262 → 214222 → 211222 → 111222 → 111111 214267\rightarrow 214262\rightarrow 214222\rightarrow 211222\rightarrow 111222\rightarrow 111111 214267→214262→214222→211222→111222→111111
共需要 5 步完成
【评测用例规模与约定】
对于 20 % 20 \% 20% 的数据,保证 n ≤ 1000 , h i ≤ 1 0 6 n \leq 1000, h_{i} \leq 10^{6} n≤1000,hi≤106 。
对于 100 % 100 \% 100% 的数据,保证 n ≤ 2 × 1 0 5 , h i ≤ 1 0 18 n \leq 2 \times 10^{5}, h_{i} \leq 10^{18} n≤2×105,hi≤1018 。
思路:
本题是一个最长公共下降子序列的问题,对于任意一个 h h h ,只要它高度降到了与前一个高度下降过程中的公共值,那么它就不需要花费代价继续下降。如果它降得的当前高度与前一个高度没有公共值,则需要多花费一个代价,来降低自己的高度。
如何把公共值计算出来?
用 s e t set set 来记录上一个位置降到 1 1 1 时的所有中间值,即公共值。
下图是该算法模拟的样例:
C++代码:
#include ——完结撒花—— \color{Red}{——完结撒花——} ——完结撒花——

![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-fEh1nPBa-1680352873066)(统计子矩阵.png)]](http://img.e-com-net.com/image/info8/a7e2f4d7c58845f98b9386549e0a5c5f.png)