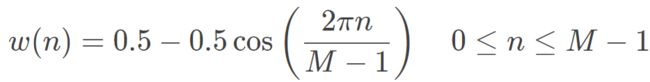PySOT代码之SiamRPN++分析——基础知识：hanning、outer、tile、contiguous、flatten、meshgrid、torch.nn.Parameter

 

基础知识扩充

感谢大佬们的工作，许多内容都是直接拿来用的，原地址附在参考文献板块

np.hanning(M)

汉宁窗是通过使用加权余弦形成的锥形

• M：整数，输出窗口中的点数。如果为零或更小，则返回一个空数组
• out：返回一个汉宁窗口，形状为（M，），最大值归一化为1（只有M为奇数时才出现该值），由下列公式计算得到：

>>> np.hanning(11)
array([0.       , 0.0954915, 0.3454915, 0.6545085, 0.9045085, 1.       ,
       0.9045085, 0.6545085, 0.3454915, 0.0954915, 0.       ])
# 以下来自官网例子：
>>> import matplotlib.pyplot as plt
>>> window = np.hanning(51)
>>> plt.plot(window)
[]
>>> plt.title("Hann window")
Text(0.5,1,'Hann window')
>>> plt.ylabel("Amplitude")
Text(0,0.5,'Amplitude')
>>> plt.xlabel("Sample")
Text(0.5,0,'Sample')
>>> plt.show()

np.outer(a,b,out=None)

numpy中的向量相乘，向量a,b，假设a = [a0, a1, …, aM]和b = [b0, b1, …, bN]，那么输出数组为：out[i, j] = a[i] * b[j

---

补充说明：

• np.dot()如果碰到的是秩为1的数组，那么执行的是对应位置的元素相乘再相加;如果遇到的是秩不为1的数组，那么执行的是矩阵相乘。但是需要注意的是矩阵与矩阵相乘是秩为2，矩阵和向量相乘秩为1。
• np.multiply()表示的是数组和矩阵对应位置相乘。
• np.outer()表示的是两个向量相乘。也就是[n*m]*[m*n]=[n*n]
• *（乘号）对数组执行的是对应位置相乘，对矩阵执行的是矩阵相乘。

注：数组和矩阵在numpy中的区别是np.array和np.mat的区别

np.tile(A,reps)

• 输入数组A，reps指定沿A各个轴axis扩展的倍数，输出矩阵维数是max(d, A.ndim)，其中d是reps的长度
• 当d与A.ndim的维数不相等的时候，就把那个维数小的一方前面插入维度，值为1，然后A沿第一个轴方向到最后的轴，对应reps里面的值进行对应axis的扩展，注意：这里不是单行单列的repeat，而是整体的扩展，可以对照numpy.repeat学习

np.tile(mat, (1, 4))=np.tile(mat,4)

将原mat横向复制1次纵向复制4次，返回结果为1*4的矩阵

contiguous()

contiguous()一般在permute()等改变形状和计算返回的tensor后面，因为改变形状后，有的tensor并不是占用一整块内存，而是由不同的数据块组成，而tensor的view()操作依赖于内存是整块的，这时只需要执行contiguous()这个函数，把tensor变成在内存中连续分布的形式。

flatten()

将array或mat拉成1维（mat有空）

np.meshgrid()

mesh 点云，grid 网格，该函数生成的是坐标点，返回x,y的array，实际上可看作两个集合作笛卡尔积，然后把对应元素放到对应位置。

• 输入是一些列1-D的array：x1, x2,…, xn。有几个最后的格点网格就是几维的，一般我们都是输入x和y，所以生成的是一张二维平面的网格
• 有一些可选参数，例如indexing : {‘xy’, ‘ij’}坐标系In the 2-D case with inputs of length M and N, the outputs are of shape (N, M) for ‘xy’ indexing and (M, N) for ‘ij’ indexing，即返回的索引顺序会不一样，sparse : bool，copy : bool

>>> nx = 5
>>> ny = 3
>>> x = np.arange(nx) - (nx - 1) / 2
>>> x
array([-2., -1.,  0.,  1.,  2.])
>>> y = np.arange(ny) - (ny - 1) / 2
>>> y
array([-1.,  0.,  1.])
>>> xv, yv = np.meshgrid(x, y) #默认indexing='xy',所以输入(5,3),输出(3,5)
>>> xv
array([[-2., -1.,  0.,  1.,  2.],
       [-2., -1.,  0.,  1.,  2.],
       [-2., -1.,  0.,  1.,  2.]])
>>> yv
array([[-1., -1., -1., -1., -1.],
       [ 0.,  0.,  0.,  0.,  0.],
       [ 1.,  1.,  1.,  1.,  1.]])
>>> xv, yv = np.meshgrid(x, y, sparse=True)  # make sparse output arrays
>>> xv
array([[-2., -1.,  0.,  1.,  2.]])
>>> yv
array([[-1.],
       [ 0.],
       [ 1.]])
>>> xv, yv = np.meshgrid(x, y, indexing='ij')
>>> xv
array([[-2., -2., -2.],
       [-1., -1., -1.],
       [ 0.,  0.,  0.],
       [ 1.,  1.,  1.],
       [ 2.,  2.,  2.]])
>>> yv
array([[-1.,  0.,  1.],
       [-1.,  0.,  1.],
       [-1.,  0.,  1.],
       [-1.,  0.,  1.],
       [-1.,  0.,  1.]])

 

torch.nn.Parameter()

class Parameter(data: Tensor=..., requires_grad: builtins.bool=...)是Ternsor的子类，它在自定义Module里有特殊的功能，自动注册到parameters里，且它初始化默认 requires_grad=True。 可以把Parameter看成Tensor。

可以把这个函数理解为类型转换函数，将一个不可训练的类型Tensor转换成可以训练的类型parameter并将这个parameter绑定到这个module里面(net.parameter()中就有这个绑定的parameter，所以在参数优化的时候可以进行优化的)，所以经过类型转换这个变量变成了模型的一部分，成为了模型中根据训练可以改动的参数了。使用这个函数的目的也是想让某些变量在学习的过程中不断的修改其值以达到最优化。linear里面的weight和bias就是parameter类型，且不能够使用tensor类型替换，还有linear里面的weight甚至可能通过指定一个不同于初始化时候的形状进行模型的更改。

参考文献

https://blog.csdn.net/laizi_laizi/article/details/104601908

https://www.jianshu.com/p/732155374570

https://blog.csdn.net/laizi_laizi/article/details/104442539

https://www.jianshu.com/p/d8b77cc02410