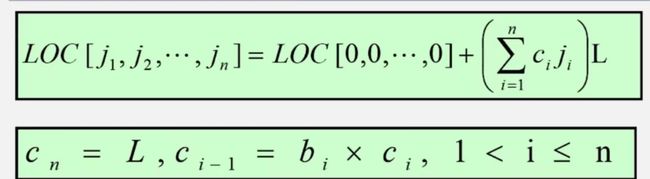数据结构——数组

目录

定义

数组的抽象数据类型定义

二维数组

存储方式

顺序存储

一维数组

二维数组

三维数组

n 维数组

特殊矩阵的压缩存储

对称矩阵

三角矩阵

对角矩阵（带状矩阵）

稀疏矩阵

---

定义

数组：按一定格式排列起来的，具有相同类型的数据元素的集合

一维数组：若线性表中的数据元素为非结构的简单元素，则称为一维数组

一维数组的逻辑结构：线性结构，定长的线性表

声明格式：

     数据类型 变量名称[长度]

二维数组：若一维数组中的数据元素又是一维数组结构，则称为二维数组

二维数组的逻辑结构：

• 线性结构 定长线性表：该线性表的每个数据元素也是一个定长的线性表
• 非线性结构：每个数据元素即在一个行表中，又在一个列表中

声明格式：

     数据类型 变量名称[行数][列数]

C 中，一个二维数组类型可以定义为一维数组类型（其分量类型为一维数组类型），即

typedef elemtype array2[m][n];

等价于：

typedef elemtype array1[n];
typedef elemtype array2[m];

三维数组：若二维数组中的元素又是一个一维数组，则称作三维数组

n 维数组：若 n-1 维数组中的元素又是一个一维数组结构，则称作 n 维数组

结论：线性表结构是数组结构的一个特例，而数组结构又是线性表结构的扩展

数组特点：结构固定——定义后，维度和维界不再改变

数组的基本操作：除了结构的初始化和销毁之外，只有取元素和修改元素值的操作

数组的抽象数据类型定义

ADT Array{

    数据对象：=0,...,,i=1,2,...,n,

        D={  | n(>0)称为数组的维数, 是数组第 i 维的长度, 是数组元素的第 i 维下标, ∈ElemSet }

    数据关系：R={R1,R2,...Rn}

                      Ri={<> |

                                 0 ≤  ≤ , 1 ≤ k ≤ n 且 k ≠ i ,

                                 0 ≤  ≤  ,

                                  ,  ∈ D，i = 2,...,n }

    基本操作：

        InitArray(&A,n,bound1,...,boundn)

            操作结果：若维数 n 和各维长度合法，则构造相应的数组 A，并返回 OK。

        DestroyArray(&A)

               操作结果：销毁数组 A

        Value(A,&e,index1,...,indexn)

               初始条件：A 是 n 维数组，e 为元素变量，随后是 n 个下标值

               操作结果：若各下标不超界，则 e 赋值为所指定的 A 的元素值，并返回 OK。 

        Assign(&A,e,index1,...,indexn)

               初始条件：A 是 n 维数组，e 为元素变量，随后是 n 个下标值

               操作结果：若下标不超界，则将 e 的值赋给所指定的 A 的元素，并返回 OK。

}ADT Array

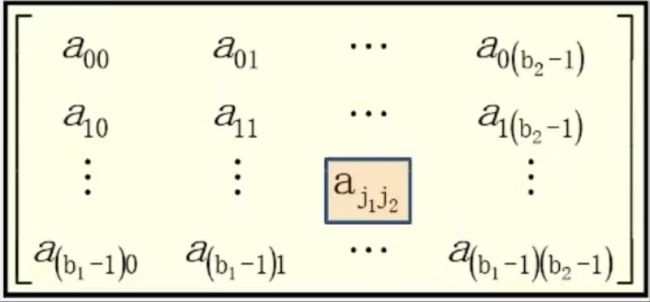
二维数组

n=2，维数为2，二维数组

b1：第 1 维长度    b2：第 2 维长度

：第 1 维下标为 ，第 2 维下标为 

数据对象：D={  | 0 ≤  ≤ ，0 ≤  ≤  }

数据关系：R={ ROW , COL }

                       ROW={ <  ,  > | 0 ≤  ≤ ，0 ≤  ≤  }

                       COL={ <  ,  > | 0 ≤  ≤ ，0 ≤  ≤  }

存储方式

数组特点：结构固定——维数和维界不变

数组基本操作：初始化、销毁、取元素、修改元素值，一般不做插入或删除操作，所以，一般采用顺序存储结构表示数组

顺序存储

       数组可以是多维的，但存储数据元素的内存单元地址是一维的，因此，在存储数组结构之前，需将多维关系映射到一维关系。

一维数组

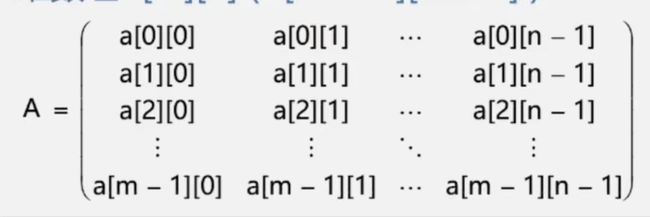
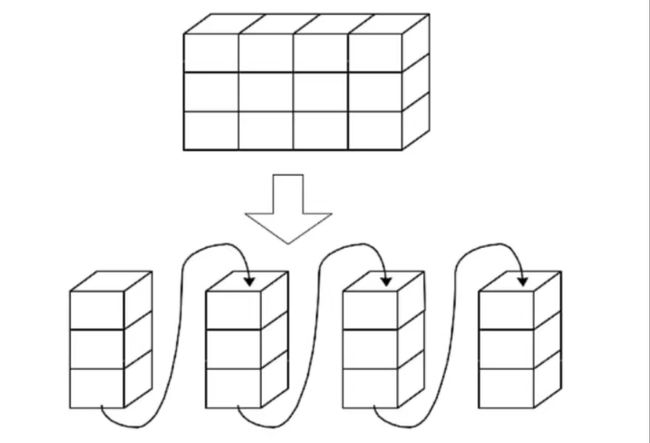
二维数组

两种顺序存储方式：

• 以行序为主序（低下标优先）：C，PASCAL，JAVA，Basic
• 以列序为主序（高下标优先）：FORTRAN

数列：A[m][n]

A=(  )( p=m或n )

 1 ≤ i ≤ m   以行序为主序

1 ≤ j ≤ n   以列序为主序

以行序为主序

       设数组开始存储位置 LOC(0,0)，存储每个元素需要 L 个元素单元，数组元素 a[i][j] 的存储位置是：LOC(i,j)=LOC(0,0)+(n*i+j)*L【n*i+j 是在 a[i][j] 前面所有元素的个数】

以列序为主序

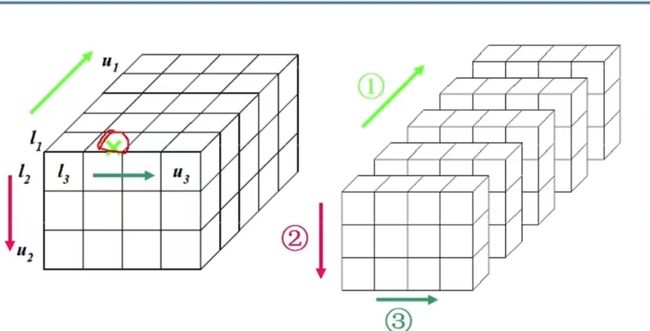
三维数组

按页/行/列存放，页优先的顺序存储

a[m1][m2][m3] 各维元素个数为 m1,m2,m3

下标为 i1,i2,i3 的数组元素的存储位置：

LOC(i1,i2,i3)=a+i1*m2*m3+i2*m3+i3   a 为指针，不需要 *L

i1*m2*m3：前 i1 页总元素个数

i2*m3：第 i1 页的前 i2 行总元素个数

i3：第 i2 行前 i3 列元素个数

n 维数组

特殊矩阵的压缩存储

矩阵：一个由 m*n 个元素排成的 m 行 n 列的表

矩阵的常规存储：将矩阵描述为一个二维数组

矩阵的常规存储特点：

• 可以对其元素进行随机存取
• 矩阵运算非常简单，存储密度为 1

不适宜常规存储的矩阵：值相同的元素很多且呈某种规律分布；零元素多

矩阵的压缩存储：为多个相同的非零元素只分配一个存储空间；对零元素不分配空间

压缩存储：若多个数据元素的值相同，则只分配一个元素值的存储空间，且零元素不占存储空间

可压缩的矩阵：一些特殊的矩阵，如：对称矩阵、对角矩阵、三角矩阵、稀疏矩阵

稀疏矩阵：矩阵中非零元素的个数较少（一般小于5%）

对称矩阵

特点：在 n*n 的矩阵 a 中，满足  ( 1 ≤ i,j ≤ n )

存储方式：只存储下（或者上）三角（包括主对角线）的数据元素，共占用 n*(n+1)/2 个元素空间

三角矩阵

特点：对角线以下（或者以上）的数据元素（不包括对角线）全部为常数 C

存储方法：重复元素 C 共享一个元素存储空间，共占用 n*(n+1)/2+1 个元素

对角矩阵（带状矩阵）

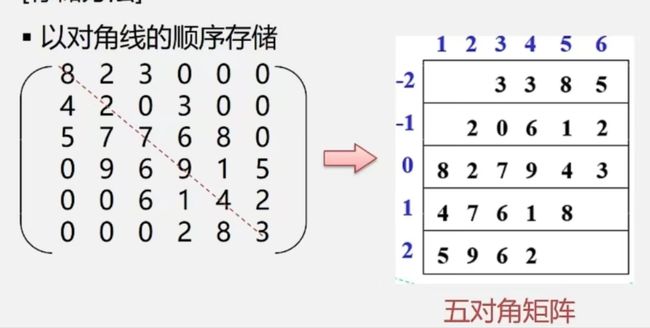
特点：在 n*n 的方阵中，所有非零元素都集中在以对角线为中心的带状区域中，区域外的值全为 0，则称为对角矩阵。常见的有三对角矩阵、五对角矩阵、七对角矩阵……

存储方法：对角线的顺序存储

稀疏矩阵

设在 m*n 的矩阵中有 t 个非零元素。令 δ=t/(m*n) ，当 δ ≤ 0.05 时称为稀疏矩阵

三元组（i，j，）唯一确定矩阵的一个非零元素

压缩存储原则：存各非零元的值、行列位置和矩阵的行列数

三元组的不同表示方法可决定稀疏矩阵不同的压缩存储方法

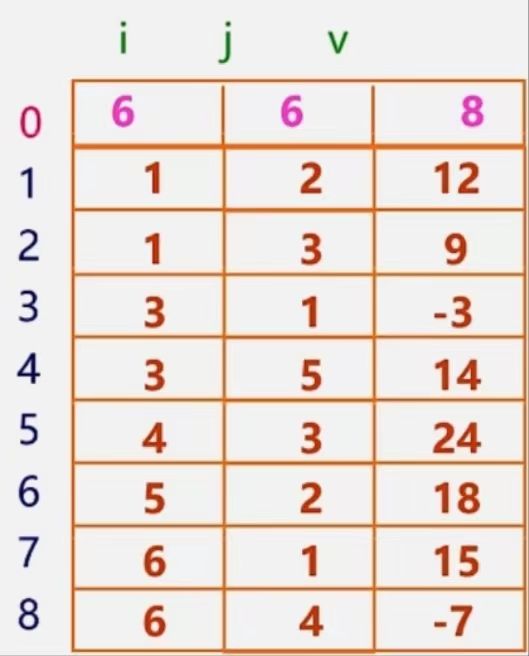
顺序存储——三元组顺序表

为更可靠描述，通常加一个“总体”信息：即总行数、总列数、非零元素总个数

三元组顺序表又称有序的双下标法

三元组顺序表的优点：非零元在表中按行序有序存储，因此便于进行依行顺序处理的矩阵运算

三元组顺序表的缺点：不能随机存取，若按行号存取某一行中的非零元，则需从头开始进行查找

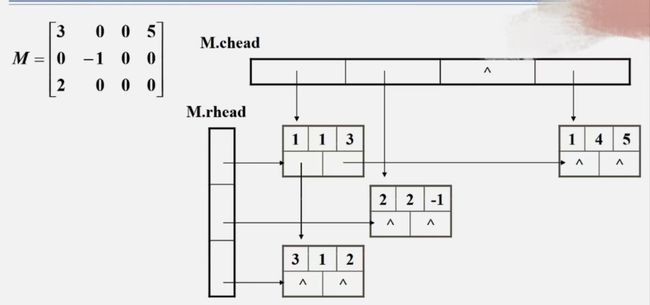
链式存储——十字链表

优点：能够灵活地插入因运算而产生的新的非零元素，删除因运算而产生的新的零元素，实现矩阵的各种运算

在十字链表中，矩阵的每一个非零元素用一个结点表示，该结点除了(row,col,value)以外，还要有两个域：

• right：用于连接同一行中的下一个非零元素
• down：用于连接同一列中的下一个非零元素

十字链表中结点的结构示意图：